Приближенное решение ду с помощью степенных рядов
1.Способ последовательного дифференцирования
Пусть требуется решить ур-е
(1)
удовл.условиям
,
(2)
Реш-е
ур-я (1) ищем в виде ряда Тейлора
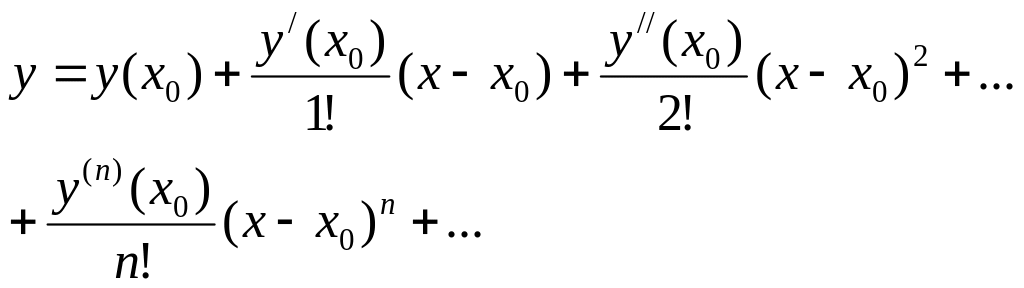(3)
при
этом первые 2 коэффициента находим из
нач. условий (2). Подставив в ур-е (1)
значения
,
,
находим
3-ий коэффициент:
Значения
,
,…находим
путем последоват.дифференцирования
ур-я (1) по X и вычиления
производных при
(коэффициентов), их подставляем в
равенство (3). Ряд ( 3) представляет искомое
частное реш-е ур-я (1) для тех значений
X, при к-рых он сходится.
Частичная сумма этого ряда будет
приближенным реш-ем ДУ (1).
2.Способ неопределенных коэфф.
Пусть требуется решить ур-е
(1)
с
нач.условиями
Предполагая,
что коэффициенты
,
и свободный член
разлаг.в ряды по степеням
, сходящ. в некотором интервале
, искомое реше-е
ищем в виде ряда
(2)
с неопределенными коэффициентами.
и
определяются при помощи нач.усл.
.
Для
нахожд.последующих коэффициентов
дифференцируем ряд (2) 2 раза и подставляем
выр-я для ф-ии Y и ее
производных в ур-е (1), заменив
их разложениями. Получаем тождество,
из к-рого методом неопред.коэфф. находим
недостающие коэфф. Построенный ряд (2)
сход. в том же интервале
и служит реш-ем ур-я (1).
14. Тригонометрическая система функций и ее свойства.
Тригонометрическя система функций - система вида 1,cosx, sinx, cos2x, sin2x, cos3x,
sin3x, … cosnx, sinnx. Система периода с T=2π
Рассмотрим на отрезке [-π;π]
Свойства:
1)
2)
от
квадрата любой функции ≠0
Одновременно 2-мя свойствами система не обладает.
15. Тригонометрический ряд. Сходимость. Ряд Фурье. Коэффициенты Фурье.
С помощью тригонометрического ряда практически любую периодическую функцию можно представить в виде ряда, членами которого являются простые гармоники.
Тригонометрическим рядом - называется функциональный ряд вида
т.е.
(1)
Где
,
,
(n=1,2,…)называются
коэффициентами ряда.
Будем считать, что ряд равномерно сходится. Интегрируем правую и левую части:
Отсюда:
Домножим
обе части равенства (1) на
и
проинтегрируем обе части:
При
m=n получим:
Отсюда:
,
n=1,2,3,…
Аналогично,
умножив равенство (1) на
и проинтегрировав почленно на отрезке
[
],
найдём
,
n=1,2,3,…
16.Разложение в ряд Фурье периодических функций с периодом 2п.
1. Пусть ф-ция f(x) – четная, т. е. f(-x)=f(x).
Значит:
;
;
.
Ряд Фурье для четных ф-ций – ряд только по косинусам
2. Пусть ф-ция f(x) – нечетная, т. е. f(-x)=-f(x).
Значит:
;
;
.
Ряд Фурье для четных ф-ций – ряд только по синусам
17.Разложение в ряд функций с периодом 2 l.
Пусть f(х) есть периодическая функция с периодом 2l, вообще говоря, отличным от 2π. Разложим ее в ряд Фурье.
Сделаем
замену переменной по формуле:
.
Тогда
функция
будет периодической функцией от t
с периодом 2π. Ее можно разложить в ряд
Фурье на отрезке
:
где
Возвратимся теперь к старой переменной х:
Тогда будем иметь:
18.Разложение в ряд Фурье четных и нечетных функций.
1. Пусть ф-ция f(x) – четная, т. е. f(-x)=f(x).
Значит:
;
;
.
Ряд Фурье для четных ф-ций – ряд только по косинусам
2. Пусть ф-ция f(x) – нечетная, т. е. f(-x)=-f(x).
Значит:
;
;
.
Ряд Фурье для четных ф-ций – ряд только по синусам
19.Разложение в ряд Фурье непериодических функций.
Пусть ф-ция f(x) непереодич., заданная на [a,b].
Вместо
функции f(x)
рассматривают ф-цию
с периодом 2l, причем [a,b]
и на [a, b]
ф-ция
совпадает
с функцией f(x).
Поскольку функция периодическая то ее разлагают в ряд Фурье.
Рассмотрим один важный случай: пусть функция f(x) задана на интервале (0, l) . Ее надо доопределить на интервале (-l , 0). Можно доопределить четным образом. В этом случае мы получаем ряд Фурье только по косинусам.
Можно доопределить нечетным образом. Получим ряд Фурье только по синусам.