5. Знакопеременные ряды. Теорема о сходимости знакопеременного ряда.Абсолютная и условная сходимость знакопеременных рядов. Свойства абсолютно сходящихся рядов.
Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.
Теорема1.
Если знакопеременный ряд (1)
таков, что ряд, составленный из абсолютных
величин его членов (2)
сходится, то и данный знакопеременный
ряд также сходится.
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов. Если же знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов расходится, то данный ряд называется условно сходящимся.
Основные свойства абсолютно сходящихся рядов
1. Если ряд абсолютно сходится и имеет сумму S, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму S, что и исходный ряд (теорема Дирихле).
2.
Абсолютно сходящиеся ряды с суммами
и
можно почленно складывать (вычитать).
В результате получается абсолютно
сходящийся ряд, сумма которого равна
+
(ИЛИ соответственно
-
),
3.
Под произведением двух рядов
и
понимают
ряд вида
Произведение двух абсолютно сходящихся рядов с суммами и есть абсолютно сходящийся ряд, сумма которого равна
Таким образом, абсолютно сходящиеся ряды суммируются, вычитаются, перемножаются как обычные ряды. Суммы таких рядов не зависят от порядка записи членов.
В случае условно сходящихся рядов соответствующие утверждения (свойства), вообще говоря, не имеют места.
6. Функциональные ряды. Сходимость и сумма ряда. Область сходимости.
Функ. ряд – ряд,члены которого являются функ. одного и того же аргумента.
Ф.р.:
Совокупность значений x, при которых ф.ряд сходится - область сходимости ф.ряда.
;
-
n-частичная сумма ,
-
остаточный член
=lim
Если ряд сходится, то
7. Равномерная сходимость функциональных рядов. Признак Вейерштрасса.
О
пределение
(равномерной последовательности на
множестве E
D функциональной последовательности):
Ф.р.
называется
равномерно сходящимся, если задав любое
>0
можно указать такой N>0, что для всех
n>N будет выполнятся неравенство
Критерий
Коши:
Определение равномерной сходимости функционального ряда на множестве E:
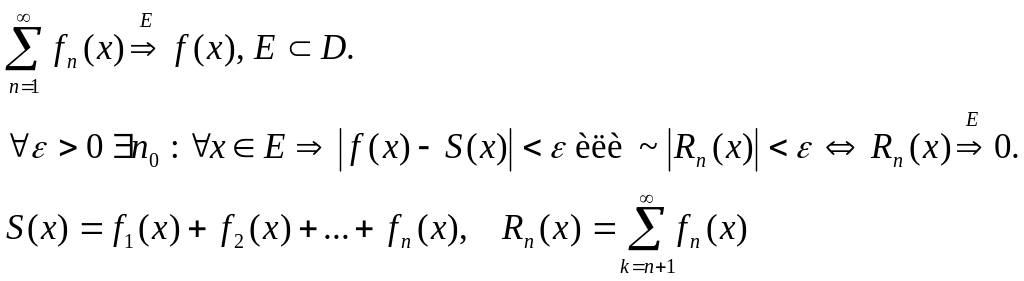
Критерий Коши:
.
Следствие. Если
Признак равномерной сходимости.
1) Признак Вейерштрасса (мажорантный признак)
П
усть
дан функциональный ряд
и если
– сходится, то функциональный ряд
сходится равномерно на E.
Д
оказательство
(по критерию Коши):
Т.к. ряд сходится, то по критерию Коши: для
любого
ε>0 существует такой номер N, что
ε для всех n>N и любых целых p>=0.
Поэтому для всех n>N и
.
Это означает, что ряд
сходится равномерно на множестве Е
8. Интегрирование и дифференцирование функциональных рядов.
И
нтегрирование
и дифференцирование функциональных
рядов.
Пусть имеется ряд (1)
Теорема о интегрировании и дифференцировании: Если ряд состоящий из непрерывных функций, сходится равномерно на [а, b] к сумме S(x), то интеграл от суммы этого ряда = сумме интегралов от его членов.
, где α и х є [a,
b]
Д
оказательство:
|
|<ξ
По свойству определенного интеграла:
,
т.к.
Дифференцирование функциональных рядов.
Теорема
Если функциональный ряд (1)
сходится к сумме S(x)
на [a, b], и ряд (2)
,
составленный из производных членов
данного ряда равномерно сходится на
[a, b] к сумме
σ(x), то сумма ряда,
составленного из производных, равна
производной от суммы ряда (1), т.е. σ(x)=
Доказательство: Т.к. 2-ой ряд сходится равномерно на [a, b], то по теореме интегрирования функциональных рядов.
Продифференцируем
по х:
Что и требовалось доказать.