24. Эйлеровы и гамильтоновы графы.(Эйлеров граф).
1-я работа, к-рую принято связывать с теории графов появилась в 1736г. Это была курсовая работа Эйлера, когда он был студентом. В этой работе рассматривались проблемы Кеннинг-х мостов ч/з город, там протекала река, омывая 2 острова, к-рые соединены системой мостов.
Вопрос: Э ли такой маршрут прогулки, к-рый позволяет пройти по каждому мосту 1 раз и вернуться в исходную точку.
В терминологии теории графов сводится к тому:Э ли замкнутый путь, который включает в себя все ребра графа.
Опр: Путь Эйлера графа Г – это такой замкнутый путь, к-рый включает в себя все ребра графа Г.
Опр: Граф наз Эйлеровым, если он имеет по крайней мере 1 путь Эйлера.
для пути ни 1 из ребер не должно проходиться > 1 раза. Т о. путь Эйлера включает в себя каждое ребро, причем ровно 1 раз, при этом конечно вершины м/б включены >1 раза. Для связанного графа Г необходимое условие для того, чтобы граф имел путь Эйлера, является достаточно очевидным: каждая вершина графа должна иметь четную валентность. Для того, чтобы в этом убедиться предположим, что граф Г явл-ся связанным и имеет путь Эйлера. Т.к.граф Г связан последовательностью вершин Эйлера содержащей все вершины графа, откуда бы ни начинался путь, вершина должна иметь валентность кратную 2-м (одно ребро для входа, другое – для выхода), поэтому, чтобы каждое ребро проходить ровно 1 раз каждая вершина должна иметь четную валентность. Эйлер также доказал, что для связанного графа неоюходимое условие сущ-я пути Эйлера является также и достаточным.
Т: Связанный граф Г является Эйлеровым, если только каждая вершина имеет четную валентность. (Д-во см. выше).
(Гамильтонов граф)
Путь Эйлера ставит вопрос о прохождении каждого ребра только 1 раз и возвращении в исходную точку. Аналогичная проблема связана с вопросом: можно ли посетить каждую вершину только 1 раз без прохождения какого-либо из ребер 1-го раза и с возвращением в исходную точку. Эта проблема была разрешена Гамильтоном.
Опр: Гамильтонов цикл для графа Г–это цикл (простой замкнутый путь), который проходит ч/з все вершины.
Опр: Граф Г называется Гамильтоновым, если он имеет Гамильтонов цикл.
Если спецификация Эйлерова графа не вызывает трудностей, то для гамильтонова графа дело обстоит иначе. Уже >200 лет многие умы бьются над вопросом, к-рый до сих пор открыт: каковы необходимые условия, чтобы граф являлся Гамильтоновым. Понятно, что граф должен быть связанным.
25. Изоморфизм графов.
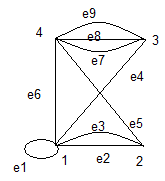
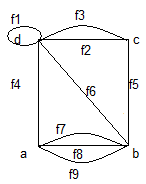
Рассмотрим 2 графа Г и Ɛ. Определенных следующим образом:
Г:{1,2,3,4},А1; Ɛ:{a,b,c,d}, А2
1 2 1 1 0 3 0 1
А1= 2 0 0 1 А2= 3 0 1 1
1 0 0 1 0 1 0 2
1 1 3 0 1 1 2 1
а)
б)
Внимательное рассмотрение рис. а) и б) позволяет сделать вывод: по сути графы Г и Ɛ одинаковы. Если мы перенумеруем вершины a,b,c,d в 3,4,2,d, а ребра fi в ei, i=1,…,9.
На рис а) и б) представлен 1 и тот же граф. Понятно, что Г и Ɛ это не одно и то же, ибо у них различны элементы множества вершин. Такие графы наз изоморфными.
Процесс переименования вершин графа Ɛ мы по сути определили биекцию между вершинами множества Г и Ɛ, причем сделали это таким образом, чтобы для элементов множеств ребер графов Г и Ɛ. Также имеет место биекция, т.е. для n ребер связанных 2-х вершин графа Г также n ребер связанными соответствующими вершинами графа Ɛ. Такое соответствие вершин и ребер наз изоморфизмом из Г в Ɛ (и наоборот).
Опр: Пусть Г и Ɛ – 2 графа. Изоморфизм из Г в Ɛ состоит в парабиекции (Ɵ,Ф). Ɵ отвечает за биекцию вершин VГ→VƐ, а Ф за ребра: ЕГ→ЕƐ,таких, что для каждого ребра е шрафа Г, если δГ(е)={V,W}, то δƐ(е)={Ɵ(V), Ɵ(W)}.
Два графа называются изоморфизмами, если существует изоморфим из Г в Ɛ.
Условие если δГ(е)={V,W}, то δƐ(е)={Ɵ(V), Ɵ(W)} гарантирует для 2-х графов 2 соответствия между элементами множеств вершин и элементами множеств ребер.
Теорема: Пусть (Ɵ,Ф) изоморфизм из Г в Ɛ,тогда:
Г и Ɛ имеют одинаковое количество вершин.
Г и Ɛ имеют одинаковое количество ребер связанности.
имеют одинаковое количество компонент.
Соответствующие вершины имеют одинаковые валентности.
Если Г простой граф, то Ɛ – также простой граф.
Если Г Эйлеров граф, то Ɛ – также Эйлеров граф.
Если Г Гамильтонов граф, то Ɛ – также Гамильтонов граф.