1.Предмет и задачи дм. Дискр величины.
Дм заявила о себе давно, более 200 лет тому назад, это примерная попытка матем-го писания простых речевых конструкций, определ-е маршрутов следования и т.д. Тем не менее высокая востребованность ДМ возникла после 2-ой Миров войны. Этосвязано с появл лаповых вычисит машин.
Что мы понимаем под словом дискретная? Этому слову м/о противопоставить слова непрерывный. Д значит способный принимать лишь некотор знач-я, при этом знач-я меняются скачком.
Где встречаются, применяются, используются Д величины? Прежде всего это комп-ры котор функционируют на основе бесконечн электрич каналов, кодируемых: 1и 0, выполнения тех или иных операций. ДМ и логика лежат в основе любого современного изучения инф-ки. Слово «дискретная» означает составление из отдельн частей, а ДМ имеет дело с совокупностью объектов назыв множествами и определ на них стр-ми. Эл-ты этих мн-в как правило изолированы др от др и геометр не связаны. Действит-но большинство интересующих нас множ-в конечны или по крайней мере счетны.
Эта обл-ть мат-ки привлекается для реш-я задачи на комп-ре в терминах аппаратных средств и программного обеспечения с привлечением организации символов и манипуляции данными. Современ цифров комп по существу конечная дискр-я система. Понимание того как такая машина работает м/о достигнуть, если представ машину как дискр матем система. Поэтому наша цель при изуч ДМ- приобрести инструменты и технику необх для понимания и проектирования комп систем. Когда и как исп-ть эти инстр и технику – это раздел матем-ки котор наз-ся мат моделированием.
Традиционно к ДМ относятся такие обл-ти математич знания, как комбинаторика, теория чисел, мат логика, теор алгоритм систем, теор графов и сетей.
2.Понятие рекурсии. Показ принципа работы рекурсии на схеме.
Опр-е: Рекур наз-ся такой способ вызова подпрограммы, когда процедура или функция вызывает саму себя. Ex: А и В.Необходимо большее из них разделить на меньшее и рез-т присвоить переменной F.
If A>=И then else F:=A/b
Else F:=B/A
В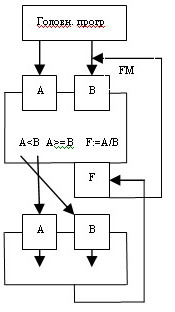
ажным
моментом при составл рекурс подпрогр
яв-ся организация выхода. Здесь легко
допустить ошибку составл в том, что
подпрограмма будет послед-но вызывать
саму себя ∞ долго, поэтому рекурс поцесс
должен шаг за шагом так упрощать задачу,
что бы в конце концов для нее появ-сь
не рекурсивн реш-е.
FM- имя подпрогр, V- заведомо вып-ся усл-е, A>=B, проэтому сразу же реализ-ся инстр-я F:=A/B
В процед FM перед-ся знач-е 2-х введ значений чисел А и В. Предположим, что А>=И в этом случае сразу же при первом же к процед FM им место нерекурсивный выход(сразу выч-ся и перед-ся в головн прогр знач-е F).
Пусть A<B, тогда прцед FM вызывает саму себя, однако переем А и В меняются местами при вызове процед FM. Парам-ру А процед FM перед-ся большее знач-е, парам-ру
В перед-ся меньш знач-е.
Program pr;
Var A, B, F:real;
functionFM(A,B:real):real; var C:real;
begin
if A<B then C:= FM(B,A)
else C:=A/B;
FM:=C
End;
Begin
Readln(A,B);
F:= FM(A,B);
Wrireln(F);
End.
Program pr;
Var A, B, F:real;
Procedure FM(A,B:real, var C:real);
begin
if A<B then FM(B,A.C)
else C:=A/B;
End;
Begin
Readln;
FM(A,B,F);
Wrireln(F);
End.
3.Рекуррентные соотношения и последовательности. Числа Фибоначчи.
Берем послед-ть 1, a, a2, a3, ...an перв множ=1, а кажд след = предыдущему умножен на знач-е а.
Переобозначим P0,P1,P2,...,Pn, тогда наша послед-ть Pi=Pi-1*a i=1,2,3,..,n такие соотношения принято назыв рекуррентными.
«Рекуррентный» означает «возвращающийся». Из курса элементарн матем-ки известны ф-лы an=an-1+d –арифм прогр. Bn=bn-1*q –геом прогр.
Посл-ть множ-ль котор удовл некотор рекуррентное соотнош-ю так же наз-ся рекур-м.
{f}1,1,2,3,5,8,13,…
F1=1,f2=1, f3=3 fn=fn-2+fn-1 при n>2 –эта посл-ть носит назв-е Фибоначчи