
- •1.Предмет и задачи дм. Дискр величины.
- •2.Понятие рекурсии. Показ принципа работы рекурсии на схеме.
- •4.Система рекуррентных соотношений
- •5. Приемы и методы решения рекуррентных соотношений.
- •6.Предмет и задачи раздела раздела матем-ки комбинаторика. Правили суммы и правило произведения.
- •7.Комбинаторика. Размещение с повторением и без повторения.
- •8.Комбинаторика. Перестановка с повтор-ем и без повтор-я.
- •9. Комбинаторика. Сочетание с повторением и сочетание без повторения
- •10. Комбинаторные задачи геом-ого содержания. Свойства чисел . Свойства чисел
- •13. Генерация подмножеств. Числа Стирлинга 2-го и 1-го рода.
- •14. Числа Каталана.
- •15. Полиномиальная формула.
- •16. Производящие функции и их применения.
- •17. Принцип включения и исключения.
- •18. Функция Эйлера. Функция Мебиуса.
- •19. Графы. Основные понятия и определения теории графов.
- •20. Матрица смежности. Валентность вершины. Матрица инцидентности.
- •21. Виды графов
- •22. Маршруты, цепи(пути) и циклы в графах.
- •23. Связные графы. Изоморфизм графов. Подграфы.
- •24. Эйлеровы и гамильтоновы графы.(Эйлеров граф).
- •25. Изоморфизм графов.
- •26. Планарные графы. Непланарность графов к5 и к3,3. Теорема Понтрягина-Куротовского.
- •27. Теорема Эйлера и ее следствия.
- •28. Деревья.
- •29. Ориентированные графы. Полный ориентированный граф.
- •30. Графы с цветными ребрами. Свойства графов с цветными ребрами.
- •31. Сетевое планирование и управление. Сетевой график.
- •32. Принципы и правила построения сетевых графиков.
- •33. Критический путь в сетевых графиках.
- •34. О резервах времени в сетевых графиках.
10. Комбинаторные задачи геом-ого содержания. Свойства чисел . Свойства чисел
=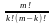 (1)
(1)
Числа -выражают количество k-элементных подмножеств данного множества Х, состоящего из m элементов, т.е. количество сочетаний без повторений из m элементов по k, обладает целым рядом замечательных свойств. Эти свойства можно доказать исходя из формулы (1). Но более содерж. явл-ся доказательства, опирающиеся на теорию множеств.
10.
Если
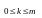 ,
то
,
то
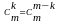 (2)
(2)
1)
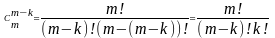
2) Смысл этого утверждения заключается в следующем:
Пусть множество Х состоит из m элементов, тогда каждому k-элементному подмножеству А множество Х соответствует однозначно определенное подмножество содержащее (m-k) элементов. Оно получается из Х удалением всех элементов подмножества А и называется дополнением к А в Х.
Любое (m-k)-элементное подмножество в множестве Х является дополнением 1! k-элементного подмножества. Значит существует взаимно-однозначное соответствие между k-элементными и (m-k)-элементными подмножествами, а потому число подмножеств этих 2-х видов одинаково. Это утверждение выражается формулой (2).
20.
Справедливо равенство
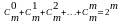 (3)
(3)
Теор: Число подмножеств m-элементного множества равно 2m.
1)
В самом деле выполняется равенство
(3). Но любое подмножество множества Х
содержит k
элементов. Т.к. число k-подмножеств
в множестве Х равно
,
то по правилу
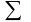 общее
число подмножеств m-элементного
множества Х равно
общее
число подмножеств m-элементного
множества Х равно
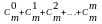 .
Сравнивая 2 полученных выражения получим
равенство (3).
.
Сравнивая 2 полученных выражения получим
равенство (3).
11. Биномиальные коэффициенты. Треугольник Паскаля. Бином Ньютона
С помощью равенства
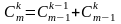 можно последовательно вычислить
.
можно последовательно вычислить
.
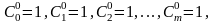
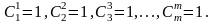
Вычисления удобно записывать в виде треугольной таблицы:
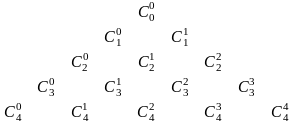

Такую таблицу называют треугольником Паскаля.
В (n+1)
строке таблицы по порядку стоят числа
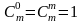 ,
а остальные числа находятся по формуле
.
Поскольку
,
а остальные числа находятся по формуле
.
Поскольку
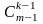 и
и
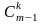 располагаются
в этой таблице строкой выше чем
и находится в верхней строке слева и
справа от
,
то для получения
надо сложить слева и справа от него
числа предыдущей строки.
располагаются
в этой таблице строкой выше чем
и находится в верхней строке слева и
справа от
,
то для получения
надо сложить слева и справа от него
числа предыдущей строки.
Числа стоящие в треугольнике Паскаля встречаются при возведении в степень 2-х-члена (a+b)n
(a+b)0=1
(a+b)1=1a+1b
(a+b)2=1a2+2ab+1b2
(a+b)3=1a3+3a2b+3ab2 +1b3
……………………………..
Продолжая такой расчет можно записать следующую гипотезу.
12. Ряд Ньютона на случай действительных показателей (n=1/2 и n=-1/2).
Пусть дано n=1/2
и n=-1/2.
Возьмем n=1/2
и наша формула примет вид:
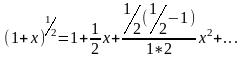
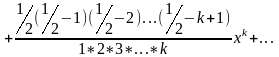 (1)
(1)
Точно также для n=-1/2
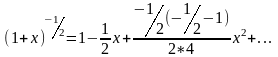
 (2)
(2)
Из (1) следует
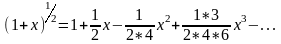
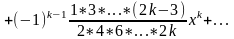 (1’)
(1’)
Сравнивая (1) и (2)
можно записать иначе для этого заметим,
что
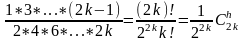 .
И так (1’) примет вид:
.
И так (1’) примет вид:
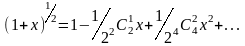
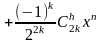 (3)
(3)
А (2) примет вид:
 +
+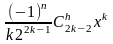
Эти выражения
сходятся в области (x)<1.
И нашему соотношению
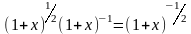 (5)
(5)
С помощью формул (3) и (4) можно извлекать квадратные корни любой точности.
13. Генерация подмножеств. Числа Стирлинга 2-го и 1-го рода.
Генерация n-элементных подмножеств m-элементного множества.
Заметим, что в
искомой последовательности n-элементных
подмножеств (каждое из которых является
возрастающей последовательностью n
чисел из диапазона 1..m)
вслед за последовательностью
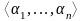 следует последовательность
следует последовательность
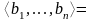
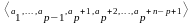 ,
где p
– максимальный индекс, для которого
bn=ap+n-p+1
,
где p
– максимальный индекс, для которого
bn=ap+n-p+1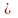 m.
Другими словами, следующая последовательность
получается из предыдущей заменой
некоторого количества элементов в
хвосте последовательности на идущие
подряд целые числа, но так, чтобы
последний элемент не превосходил m,
а первый изменяемый элемент был на 1
больше, чем соответствующий элемент в
предыдущей последовательности. Таким
образом, индекс p,
начиная с которого следует изменить
«хвост последовательности», определяется
по значению элемента A[n].
Если A[n]<m,
то нужно уменьшать индекс p:=p-1,
увеличивая длину изменяемого хвоста.
m.
Другими словами, следующая последовательность
получается из предыдущей заменой
некоторого количества элементов в
хвосте последовательности на идущие
подряд целые числа, но так, чтобы
последний элемент не превосходил m,
а первый изменяемый элемент был на 1
больше, чем соответствующий элемент в
предыдущей последовательности. Таким
образом, индекс p,
начиная с которого следует изменить
«хвост последовательности», определяется
по значению элемента A[n].
Если A[n]<m,
то нужно уменьшать индекс p:=p-1,
увеличивая длину изменяемого хвоста.
Числа Стирлинга второго рода.
Число разбиений
m-элементного
множества на n
блоков называется число Стирлинга
второго рода и обозначается s(m,n).
По определению положим, что S(m,0)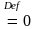 , при m>0,
S(m,m)
, при m>0,
S(m,m)
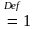 ,
S(0,0)
,
S(m,n)
при n>m.
,
S(0,0)
,
S(m,n)
при n>m.
Теорема1: S(m,n)=S(m-1,n-1)+nS(m-1,n).
Доказательство: Пусть V – множество всех разбиений множества {1,…,m} на n блоков. Положим
V1= ,
,
V2=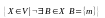 т.е. в V1
входят разбиения, в которых элемент m
образует отдельный блок, а в V2
– все остальные разбиения. Заметим,
что V2=
т.е. в V1
входят разбиения, в которых элемент m
образует отдельный блок, а в V2
– все остальные разбиения. Заметим,
что V2= .
Тогда
.
Тогда
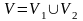 ,
,
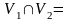 Ø.
Имеем
Ø.
Имеем
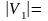 S(m-1,n-1),
S(m-1,n-1),
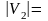 nS(m-1,n),
так как все разбиения V2
получаются следующим образом: берем
все разбиения множества {1,…,m-1}
на n
блоков (их S(m-1,n))
и в каждый блок по очереди помещаем
элемент m.
Следовательно, S(m,n)=
nS(m-1,n),
так как все разбиения V2
получаются следующим образом: берем
все разбиения множества {1,…,m-1}
на n
блоков (их S(m-1,n))
и в каждый блок по очереди помещаем
элемент m.
Следовательно, S(m,n)=

 =S(m-1,n-1)+nS(m-1,n).
=S(m-1,n-1)+nS(m-1,n).
