17. Принцип включения и исключения.

Пусть имеется N предметов, некоторые из которых обладают свойствами 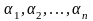при этом каждый предмет может ни обладать ни одним из этих свойств, либо обладать одним или несколькими. Def через N(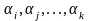 ) и может быть еще некоторыми из др. свойств. Если нам надо подчеркнуть, что берутся лишь предметы не обладающие некоторыми свойствами.

Сколько предметов ни обладают, ни одним из указанных свойств N( )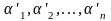

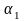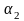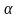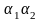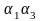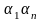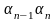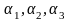Общий закон состоит в том N( )=N-N( )-N( )-…+N( )+N( )+N( )+…+N( )+…+N( 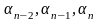)-N( )-…-N( )+…+(-1)ⁿN( )

Здесь сумма распространяется на все комбинации св-в без учета их порядка. Причем «+» ставится если число ук. свойств четное, иначе «-».

Эту формулу называют формулой включений и исключений.

Сначала исключаются все предметы обладающие хотя бы одним св-ом потом включаются предметы обладающие 2-мя из св-в.

18. Функция Эйлера. Функция Мебиуса.

Функция Эйлера ϕ (m)

Функция Эйлера ϕ(m) определяется для всех целых чисел m как количество чисел ряда 1, 2, 3, …, m взаимно простых с m. Так, ϕ(1) = 1 (по определению), ϕ(2) = 1, ϕ(3) = 2, ϕ(4) = 2, ϕ(5) = 4 и т. д. Легко показать, что для m = p – простых чисел ϕ(p) = p –1. Для m = pn функция Эйлера ϕ(pn) = pn–1(p –1). Для произвольного числа m, представленного в канонической форме, m = p1n1p2n2…psns функция Эйлера определяется следующим образом:

ϕ(m) = m(1–1/p1)(1–1/p2)…(1–1/ps).

Например, ϕ(11) = 10; ϕ(9) = 6; ϕ(18) = 6.

***

Рассмотрим частично упорядоченное множество  , где ,   

Доказать, что   

Пример.   

 

Я попытался применить обращение Мебиуса. 

Пусть  , где   - число блоков в разбиении  .  Пусть

Тогда Также можно получить, что

19. Графы. Основные понятия и определения теории графов.

Это раздел математики, особенностью которого является геометрич подход к изучению объектов. Теория графов и связанные с ней методы исследования используются на разных уровнях в математике и инф-ке. Широкое применение в таких областях как прикладная математика, прогр-е, теор алгоритмов.

Граф – это множество точек называемых вершинами и множество линий называемых ребрами, котор соединяют пары вершин или вершину саму с собой в виде дуги (петля).

Опр:(формальное): Ненаправленный граф Г это: а) конечное множество вершин V. б) конечное множество ребер Е в) функция δ; Е→Р(V).

Опр: Графом наз-ся совокупность конечного числа точек и попарно соединенных некоторых из этих точек линиями.

Опр: Граф содержащий хотя бы 2 параллельн ребра назыв мультиграфом, содержащий петли – псевдографом.

Опр: Число вершин графа называется порядком.

Опр: Ребра е1, е2,…, еn называется смешанными (инцидентными), если они имеют по крайней мере 1 общую вершину.

Опр: Валентностью (степенью вершины) называется число ребер инцидентных вершине V. Если не оговаривается особо, то петля учитывается 2-жды при подсчете валентности. Граф у котор каждая вершина имеет одинаковую валентность R, называется правильным с валентностью R или R-валентным графом.

Опр: Если степень вершины (валентность графа)=0, то вершина называется изолированной, а если=1, то наз висячей.

Опр: Нулевым графом(или полностью несвязанным графом) наз граф с пустым множеством ребер, т.е. нулевой граф это просто множество точек(вершин).

Опр: Полным графом называется граф у которого каждая пара различных вершин связана ровно одним ребром.

Опр: Граф наз двудольным, если Ǝ такое разбиение множества его вершин на 2 части(доли), что концы каждого ребра принадлежат разным частям. Если при этом любые 2 вершины, входящие в разные доли смежны, то граф наз полным двудольным.

Опр: Если на каждом ребре задано направление, указное стрелкой, то граф наз ориентированным. Если при этом каждая пара вершин соединена парой противоположно ориентированных ребер, то граф называется симметрическим.

Опр: Если совокупность вершин некоторого графа можно разелить на группы таким образом, что не существовало бы ни одного ребра соединяющего вершины разных групп, то граф наз несвязанным, если этого делать нельзя, то граф наз связанным.

Опр: Если граф ориентированный, не содержит кратных(параллельн) ребер и является связанным, то такой граф наз ассиметричным

Опр: последовательность ориентированных групп, начало каждой последней из которых совпадаютс концом предыдущего называется путем.

Опр: Вершина ассиметричного графа, в которую не входит ни одно ребро наз исток, и вершина из которого не выходит ни одно ребро наз сток.

Опр: Замкнутый путь на орграфе наз циклом.

Опр: Если ассиметричный граф не содержащий циклов имеет только 1 исток и 1 сток, то граф называется направленным. Это сетевой граф, где вершина это события, а ребра – работа.

Опр: 2 графа наз изоморфными, если вершины и ребра 1-го графа точно соответствуют вершинам и ребрам другого.(это практически один и тот же граф, но по разному изображен).