11. Уравнения прямой на плоскости – общее, в отрезках, каноническое, нормальное. Угол между прямыми. Расстояние от точки до прямой.

Общее уравнение прямой

Общее уравнение прямой линии на плоскости в декартовых координатах:

где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A,B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.

При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде :

[править]Уравнение прямой в отрезках

Прямая линия, пересекающая ось Ox в точке   и ось Oy в точке  :

В этом виде невозможно представить прямую, проходящую через начало координат.

[править]

Нормальное уравнение прямой

где p — длина перпендикуляра, опущенного на прямую из начала координат, а θ — угол (измеренный в положительном направлении) между положительным направлением оси Ox и направлением этого перпендикуляра. Если p = 0, то прямая проходит через начало координат, а угол   задаёт угол наклона прямой.

Каноническое уравнение прямой

Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое:

Вывод  [показать]

где   — координаты   и   направляющего вектора прямой,   и   координаты точки, принадлежащей прямой.

Пусть точка М₁(х₁, у₁) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М₁:

                                                                                                (1)

Координаты x₁ и у₁ могут быть найдены как решение системы уравнений:

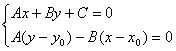
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М₀ перпендикулярно заданной прямой.

            Если преобразовать первое уравнение системы к виду:

A(x – x₀) + B(y – y₀) + Ax₀ + By₀ + C = 0,

то, решая, получим:

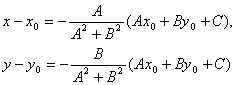
Подставляя эти выражения в уравнение (1), находим:

.

 

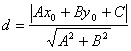Пусть прямые    и    заданы общими уравнениями    и   Обозначим через φ величину угла между прямыми    и   (напомним, что угол между прямыми измеряется от 0° до 90°), а через ψ – угол между нормальными векторами   и    этих прямых. Если ψ ≤ 90°, то φ = ψ. Если же ψ > 90°, то φ = 180° – ψ. В обоих случаях верно равенство    Из теоремы 11.10 следует, что 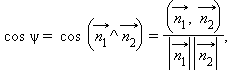  и, следовательно, 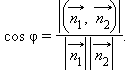  Записав через координаты, получим   

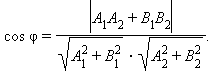
12. Уравнения прямой в пространстве. Канонические, параметрические, как пересечение двух плоскостей. Вычисление расстояния от точки до прямой, расстояния между скрещивающимися прямыми.

Канонические и параметрические уравнения прямой в пространстве

 

Пусть в декартовой системе координат дан вектор a={p,q,r} и точка М₀=(x₀,y₀,z₀).

Построим прямую l, проходящую через т. М₀, параллельную вектору a (этот вектор называютнаправляющим вектором прямой).

Утверждение 2: М  l  М₀М || a.

М₀М={x-x₀, y-y₀, z-z₀} || a    t R, т.ч. М₀М=t·a =>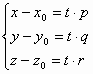 

Параметрические уравнения прямой в пространстве:

(**)

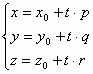Вы никогда не сталкивались с параметрическим заданием кривых? Поясним на примере: представьте себе, что по заранее намеченному маршруту с известной скоростью движется турист (автомобиль, самолёт, подводная лодка, как Вам больше понравится). Тогда, зная точку начала его путешествия, мы в любой момент времени знаем, где он находится. Таким образом, его положение на маршруте определяется всего одним параметром – временем.

В нашем случае турист движется по бесконечной прямой в пространстве, в момент времени t₀=0 он находится в точке М₀, в любой другой момент времени t его координаты в пространстве вычисляются по формулам (**).

Теперь несколько преобразуем формулы (**).

Выразим из каждой строчки параметр t: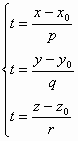 

Канонические уравнения прямой в пространстве:

Замечание 2: Эта компактная запись на самом деле содержит три уравнения.

Замечание 3: Это формальная запись и выражение вида   в данном случае допустимо.

Замечание 4: Надо понимать, что для уравнения плоскости (прямой) играет роль именно направление перпендикулярного (направляющего) вектора, а не он сам. Т.о. вполне допустимо из каких-либо соображений заменять данный (или полученный в ходе решения) вектор на пропорциональный ему. Целесообразно также упрощать полученное уравнение, деля все его коэффициенты на общий множитель.

Поскольку прямая является пересечением двух различных непараллельных плоскостей, заданных соответственно общими уравнениями:

 и 

то уравнение прямой можно задать системой этих уравнений:

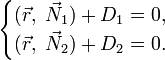
13. Некоторые задачи на прямую и плоскость в пространстве: вычисление угла между прямой и плоскостью, взаимное расположение прямой и плоскости, взаимное расположение двух прямых, построение проекции точки на плоскость и на прямую.

Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями

Р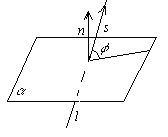 ассмотрим векторы   и  . Если угол между ними острый, то он будет  , где φ – угол между прямой и плоскостью. Тогда  .

Если угол между векторами   и   тупой, то он равен  . Следовательно  . Поэтому в любом случае  . Вспомнив формулу вычисления косинуса угла между векторами, получим  .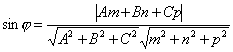

Условие перпендикулярности прямой и плоскости. Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор прямой   и нормальный вектор   плоскости коллинеарны, т.е.  .

Условие параллельности прямой и плоскости. Прямая и плоскость параллельны тогда и только тогда, когда векторы   и   перпендикулярны.

Проекция точки на прямую

Условие:

Найти проекцию точки М   на прямую   

Решение:

Составим уравнение плоскости, проходящей через точку М и перпендикулярной данной прямой. Направляющий вектор прямой   может служить вектором нормали к плоскости.

Общий вид уравнения плоскости:

Подставляем вместо   координаты вектора нормали, вместо    - координаты  точки  . Получим:

 Отсюда 

Искомая плоскость:

Точка пересечения данной прямой и полученной плоскости  будет проекцией точки М на данную прямую.

 отсюда  .

Координаты проекции:

   

Ответ: 

Ортогональной проекцией точки на плоскость называется основание перпендикуляра, опущенного из данной точки на эту плоскость.

14. Матрицы, действия с матрицами (сложение матриц, умножение на число, умножение матриц). Определители квадратных матриц порядка n: перестановки, инверсии, четность, нечетность перестановки. Определение определителя матрицы размера n через инверсии.

перестано́вка — это упорядоченный набор чисел   обычно трактуемый как биекция на множестве  , которая числу i ставит соответствие i-й элемент из набора. Число n при этом называетсяпорядком перестановки

Инверсией в перестановке π порядка n называется всякая пара индексов i,j такая, что   и π(i) > π(j).

Чётность числа инверсий в перестановке определяет чётность перестановки.

Для матрицы   справедлива формула:

,

где α₁,α₂,...,α_n — перестановка чисел от 1 до n, N(α₁,α₂,...,α_n) — число инверсий в перестановке, суммирование идёт по всем возможным перестановкам порядка n. Таким образом, в определитель войдёт n! слагаемых, которые также называют «членами определителя». Важно заметить, что во многих курсах линейной алгебры это определение даётся как основное.