
- •Программа к экзамену по алгебре и геометрии
- •2. Декартова система координат. Простейшие задачи аналитической геометрии: деление отрезка в данном отношении и координаты центра масс.
- •3. Полярные координаты, цилиндрические и сферические координаты.
- •4. Проекция вектора на ось. Свойства проекции. Скалярное произведение. Выражение через проекцию. Свойства скалярного произведения. Условие ортогональности векторов.
- •5. Левые и правые тройки векторов. Векторное произведение. Свойства.
- •6. Смешанное произведение. Свойства. Условие компланарности векторов.
- •7. Выражение скалярного, векторного и смешанного произведения в декартовой системе координат. Некоторые приложения к вычислениям объемов и площадей.
- •8. Преобразование координат на плоскости (поворот и параллельный перенос).
- •9. Уравнения линий и поверхностей. Алгебраические линии и поверхности. Теорема об инвариантности порядка. Параметрическое задание линий и поверхностей.
- •11. Уравнения прямой на плоскости – общее, в отрезках, каноническое, нормальное. Угол между прямыми. Расстояние от точки до прямой.
- •12. Уравнения прямой в пространстве. Канонические, параметрические, как пересечение двух плоскостей. Вычисление расстояния от точки до прямой, расстояния между скрещивающимися прямыми.
- •15. Свойства определителей. Минор, алгебраическое дополнение. Теорема о разложении определителя по элементам ряда.
- •18. Линейные пространства. Примеры. Линейная зависимость и независимость векторов линейного пространства. Базис. Размерность.
7. Выражение скалярного, векторного и смешанного произведения в декартовой системе координат. Некоторые приложения к вычислениям объемов и площадей.
Пусть два вектора заданы своими разложениями по ортам в декартовой системе координат
![]()
Тогда скалярное произведение
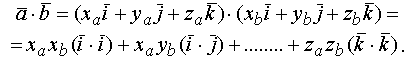
Помня, что от перестановки сомножителей скалярного произведения результат не меняется, получим
![]()
Учитывая эти результаты, найдем
![]()
Скалярное произведение векторов, заданных проекциями в декартовой системе координат, равно сумме произведений одноименных координат.
Подчеркнем еще раз, что эта формула справедлива только в ортонормированном базисе.
Косинус угла между векторами определится выражением
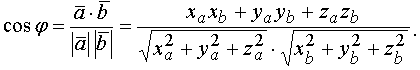
Пусть два вектора заданы своими разложениями по ортам в декартовой системе координат
![]()
Найдем векторное произведение
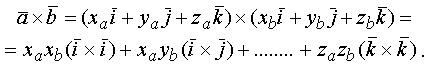
Помня, что от перестановки сомножителей векторного произведения результат меняет знак, получим
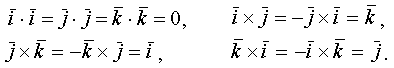
Учитывая эти результаты, найдем
![]()
или

Т.о., вектор, получаемый в результате векторного произведения векторов, заданных своими координатами, получается из определителя, первой строкой которого являются координатные орты, вторая и третья строки состоят, соответственно, из координат первого и второго сомножителей.
Пусть векторы заданы своими разложениями по ортам в декартовой системе координат
![]()
Из 3.6.2 известно, что
![]()
Скалярно
умножим этот вектор на вектор ![]() и,
учитывая свойства скалярного произведения,
получим
и,
учитывая свойства скалярного произведения,
получим
![]()
Это выражение может быть получено при вычислении определителя

по элементам третьей строки, исходя из правила вычисления определителя.
![]()
Поэтому
смешанное произведение трех векторов
обозначают как ![]() ,
не подчеркивая при этом, какая пара
векторов умножается векторно.
,
не подчеркивая при этом, какая пара
векторов умножается векторно.
8. Преобразование координат на плоскости (поворот и параллельный перенос).
Параллельный сдвиг координатных осей (рис. 4.8)
![]()
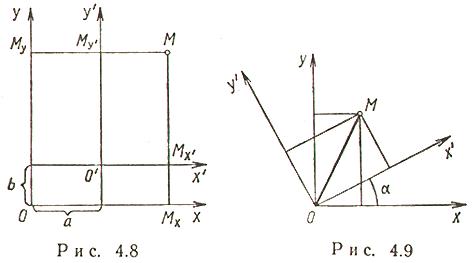
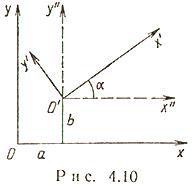
Поворот координатных осей (рис. 4.9)
![]()
Параллельный сдвиг и поворот координат осей (рис. 4.10)
![]()
9. Уравнения линий и поверхностей. Алгебраические линии и поверхности. Теорема об инвариантности порядка. Параметрическое задание линий и поверхностей.
Класс трёхмерных
параметрических поверхностей определяется функцией ![]() ,
зависящей от k параметров
и отображающей некоторое связное
множество
,
зависящей от k параметров
и отображающей некоторое связное
множество ![]() из
n-мерного пространства в
трёхмерноепространство таким
образом, что это отображение является поверхностью.
Эта функция F задаёт
класс поверхностей, а набор k параметров
- конкретную поверхность из этого класса.
из
n-мерного пространства в
трёхмерноепространство таким
образом, что это отображение является поверхностью.
Эта функция F задаёт
класс поверхностей, а набор k параметров
- конкретную поверхность из этого класса.
Наиболее практичным является случай, когда множество является единичным квадратом в двумерном пространстве. В этом случае параметрическую поверхность можно описать так:
(x,y,z)
= F(u,v) или 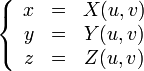 ,
где
,
где ![]()
Параметрические уравнения линии
Обозначим буквами х и у координаты некоторой точки М; рассмотрим две функции аргумента t:
![]() ,
, ![]() (1)
(1)
При изменении t величины х и у будут, вообще говоря, меняться, следовательно, точка М будет перемещаться. Равенства (1) называются параметрическими уравнениями линии, которая является траекторией точки М; аргумент t носит название параметра. Если из равенств (1) можно исключить параметр t, то получим уравнение траектории точки М в виде
F(x, y)=0.
Понятия об уравнениях линии и поверхности.
Пусть Oxy и Oxyz − афинные системы координат на плоскости и в пространстве. Уравнение
F(x, y) = 0, (5.1.1)
соответствеено
F(x, y, z) = 0, (5.1.2)
называется уравнением линии L на плоскости (поверхности π в пространстве) в заданной системе координат, если этому уравнению удовлетворяют координаты всех точек линии L (поверхности π), и только они. Очевидно, что уравнения в заданной системе координат определяют одну и ту же линию (поверхность) тогда и только тогда, когда они эквивалентны. Алгебраическим одгочленом относитеьно переменных x, y (соответственно x, y, z) с вещественным коэффициентом λ называется выражение
λ xpyq (λ xpyqzr), (5.1.3)
где p, q, r − целые неотрицательные числа. Если λ ≠ = 0, то число p + q (p + q + r) называется степенью одночлена. Алгебраическим многочленом относительно переменных x, y (x, y, z) с вещественными коэффициентами называется конечная сумма алгебраических одночленов (5.1.3). Наибольшая степень одночленов, входящих в многочлен, называется cтепенью многочлена. Линия на плоскости (поверхность в пространстве) называется алгебраической, если в некоторой аффинной системе координат она определяется уравнением (5.1.1) (соответственно (5.1.2)), где F(x, y) (соответственно F(x, y, z)) − алгебраический многочлен от переменных x, y (x, y, z) с вещественными коэффициентами. Степень многочлена F(x, y) (соответственно F(x, y, z)) называется порядком линии (поверхности). Теорема 5.1. При переходе от одной аффинной системе координат к другой алгебраическая линия (поверхность) остается алгебраической и порядок ее не изменяется. Доказательство проведем для линии. Пусть на плоскости в аффинной системе координат Oxy линия L определяеися уравнением (5.1.1), где F(x, y) − алгебраический многочлен степени n. При переходе к новой системе координат O'x'y'уравнение (5.1.1) преобразуется в уравнение F'( x', y') = 0. Покажем, что F'(x', y') − тоже алгебраический многочлен и его степень n' = n. Для этого вкаждый одночлен λ xpyq многочлена F(x, y) вместо x и y подставим их выражения через x', y'согласно формулам преобразования координат . Тогда λ xpyq = λ(с11x' + с12y' + α)p(с21x' + с22y' + β)q. Следовательно, одночлен λ xpyq преобразуется в алгебраический многочлен от переменных xp, yq, степень которого не превосходит p + q. При этом многочлен F(x, y) преобразуется в алгебраический многочлен F'(x', y'), степень которого n' ≤ n. Если в этих рассуждениях поменять ролями системы координат, то получим, что n ≤ n', т.е. n' = n. Теорема доказана.
10. Плоскость. Виды уравнений плоскости. Признаки параллельности, перпендикулярности плоскостей. Вычисление угла между плоскостями и расстояния от точки до плоскости. Нормальное уравнение плоскости. Отклонение точки от плоскости.
Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки.
Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.
Общее уравнение (полное) плоскости
![]()
где ![]() и
и ![]() —
постоянные, причём
—
постоянные, причём ![]() и
и ![]() одновременно
не равны нулю; в векторной форме:
одновременно
не равны нулю; в векторной форме:
![]()
где ![]() —
радиус-вектор точки
—
радиус-вектор точки ![]() ,
вектор
,
вектор ![]() перпендикулярен
к плоскости (нормальный
вектор). Направляющие косинусы вектора
перпендикулярен
к плоскости (нормальный
вектор). Направляющие косинусы вектора ![]() :
:
![]()
![]()
![]()
Если
один из коэффициентов в уравнении
плоскости равен нулю, уравнение
называется неполным.
При ![]() плоскость
проходит через начало
координат,
при
плоскость
проходит через начало
координат,
при ![]() (или
(или ![]() ,
, ![]() )
П. параллельна оси
)
П. параллельна оси ![]() (соответственно
(соответственно ![]() или
или ![]() ).
При
).
При ![]() (
(![]() ,
или
,
или ![]() )
плоскость параллельна
плоскости
)
плоскость параллельна
плоскости ![]() (соответственно
(соответственно ![]() или
или ![]() ).
).
Уравнение плоскости в отрезках:
![]()
где ![]() ,
, ![]() ,
, ![]() —
отрезки, отсекаемые плоскостью на
осях
—
отрезки, отсекаемые плоскостью на
осях ![]() и
.
и
.
Уравнение
плоскости, проходящей через
точку ![]() перпендикулярно
вектору нормали
перпендикулярно
вектору нормали ![]() :
:
![]()
в векторной форме:
![]()
Уравнение
плоскости, проходящей через три заданные
точки ![]() , не
лежащие на одной прямой:
, не
лежащие на одной прямой:
![]()
(смешанное произведение векторов), иначе
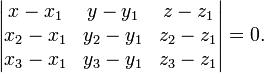
Нормальное (нормированное) уравнение плоскости
![]()
в векторной форме:
![]()
где ![]() -
единичный вектор,
-
единичный вектор, ![]() —
расстояние П. от начала координат.
Уравнение (2) может быть получено из
уравнения (1) умножением на нормирующий
множитель
—
расстояние П. от начала координат.
Уравнение (2) может быть получено из
уравнения (1) умножением на нормирующий
множитель
![]()
(знаки ![]() и
противоположны).
и
противоположны).
Две плоскости являются либо параллельными, либо пересекаются по прямой.
Прямая либо параллельна плоскости, либо пересекает ее в одной точке, либо находится на плоскости.
Две прямые, перпендикулярные одной и той же плоскости, параллельны друг другу.
Две плоскости, перпендикулярные одной и той же прямой, параллельны друг другу.
Расстояние от точки до плоскости
Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.
Отклонение
точки ![]() от
плоскости заданной нормированным
уравнением
от
плоскости заданной нормированным
уравнением ![]()
![]()
![]() ,если
,если ![]() и
начало координат лежат по разные стороны
плоскости, в противоположном случае
и
начало координат лежат по разные стороны
плоскости, в противоположном случае ![]() .
Расстояние от точки до плоскости равно
.
Расстояние от точки до плоскости равно ![]()
Расстояние ![]() от
точки
от
точки ![]() ,
до плоскости, заданной уравнением
,
до плоскости, заданной уравнением ![]() ,
вычисляется по формуле:
,
вычисляется по формуле:
![]()
[править]Расстояние между параллельными плоскостями
Расстояние
между плоскостями, заданными
уравнениями ![]() и
и ![]() :
:
![]()
Расстояние
между плоскостями, заданными
уравнениями ![]() и
и ![]() :
:
![]()
[править]Связанные понятия
Угол между двумя плоскостями. Если уравнения П. заданы в виде (1), то
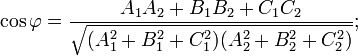
Если в векторной форме, то
![]()
Плоскости параллельны, если
![]() или
или ![]() (Векторное
произведение)
(Векторное
произведение)
Плоскости перпендикулярны, если
![]() или
или ![]() .
(Скалярное произведение)
.
(Скалярное произведение)
Пучок плоскостей — уравнение любой П., проходящей через линию пересечения двух плоскостей
![]()
где α и β — любые числа, не равные одновременно нулю.
