
- •Взаимодействие токов. Закон Ампера.
- •Билет 5. Вектор электрического смещения. Теорема Гаусса для вектора электрического смещения.
- •Билет 6.2.
- •Билет 9.2.
- •Билет №17.1
- •Билет 18.1. Уравнения Максвелла
- •Билет №19.1.
- •21.1 Понятие о классической электронной теории металлов. Закон Ома.
- •Билет 22. Закон Био - Савара. Поле прямого тока.
- •Билет 22.2
- •Билет №23.1.
- •Билет 23.2. Уравнения Максвелла
- •24.1 Энергия магнитного поля. Плотность магнитной энергии.
Билет 1.Поле неподвижных зарядов в вакууме. Взаимодействие заряженных тел. Точечные заряды. Закон Кулона. Притягиваются и отталкиваются. Точечный заряд – заряд, сосредоточенный на теле, линейные размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми он взаимодействует (принято для упрощения). Закон Кулона: сила взаимодействия между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам и обратно пропорциональна квадрату расстояния между ними: F=k|q1q2|/r2. Сила F (Кулоновская) направлена по прямой, соединяющей взаимодействующие заряды, т.е.является центральной, и соответствует притяжению (F<0) в случае ± и отталкиванию (F>0) в случае ++ и --. В векторной форме: F12=kq1q2r12/r2r. F21=F12. В СИ k=1/(4πε0)=9·109 Н·м2/Кл2, м/Ф. ε0=8,85·10-12 Кл2/(Н·м2), Ф/м. В случае нескольких тел: F1=-kΣq1q2r1i/r1i2r1i.
Билет
1.2. Вынужденные
электрические колебания.  Чтобы
вызвать вынужденные колебания, нужно
оказывать на систему внешнее периодически
изменяющееся воздействие. В случае
электрических колебаний это можно
осуществить, включив последовательно
с элементами контура переменную э.д.с.
или, разорвав контур, подать на
образовавшиеся контакты переменное
напряжение. Подадим напряжение
Чтобы
вызвать вынужденные колебания, нужно
оказывать на систему внешнее периодически
изменяющееся воздействие. В случае
электрических колебаний это можно
осуществить, включив последовательно
с элементами контура переменную э.д.с.
или, разорвав контур, подать на
образовавшиеся контакты переменное
напряжение. Подадим напряжение
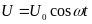 .
Уравнение Кирхгофа для этого контура:
.
Уравнение Кирхгофа для этого контура:
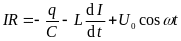 .
Разделим на L
и произведем замены:
.
Разделим на L
и произведем замены: 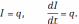 Получим:
Получим: 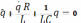 .
.
 ,
, 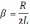 .=>
.=>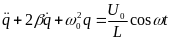 .
Решением этого уравнения является
функция:
.
Решением этого уравнения является
функция:  .
Подставим
.
Подставим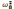 ,
,
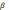
 Сила тока в контуре
Сила тока в контуре
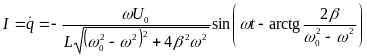 .
Напряжение в катушке
.
Напряжение в катушке
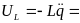
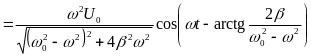 .
Напряжение на обкладках конденсатора
.
Напряжение на обкладках конденсатора
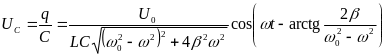 .
.
Для
заряда резонансная частота
 .
.
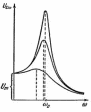
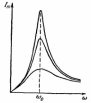
Резонансные кривые (это графики зависимостей от частоты ω внешней э.д.с. амплитуд
следующих
величин: тока I,
заряда q
на конденсаторе и напряжений
Амплитуда
максимальна при =0. => , где 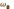 -
собственная частота контура.
-
собственная частота контура.
Максимум
при резонансе оказывается тем выше и
острее, чем меньше коэффициент затухания
Для напряжения
(как и для заряда) при резонансные кривые сходятся в одной
точке с ординатой
резонансные кривые сходятся в одной
точке с ординатой 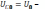 напряжению,
возникающему на конденсаторе при
подключении его к источнику постоянного
напряжения
напряжению,
возникающему на конденсаторе при
подключении его к источнику постоянного
напряжения 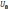 .
Максимум при резонансе получается тем
выше и острее, чем меньше
.
Максимум при резонансе получается тем
выше и острее, чем меньше 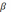 .
.
Билет 2. Электрическое поле. Напряженность электрического поля. Поле точечного заряда. Принцип суперпозиции полей. Если в пространство, окружающее электрический заряд, внести другой заряд, то на него будут действовать кулоновские силы. Значит, в пространстве, окружающем электрические заряды, существует силовое поле. Электрическое поле – поле, посредством которого взаимодействуют электрические заряды. Для обнаружения эл.п используют пробный точечный положительный заряд – не вызывающий искажения поля. Если в поле, создаваемое зарядом Q, поместить пробный заряд Q0, то на него действует сила F, различная в разных точках поля, которая, согласно закону Кулона, пропорциональна пробному заряду Q0. Поэтому отношении F/Q0 не зависит от Q0 и характеризует электростатическое поле в этой точке, где пробный заряд находится. Эта величина называется напряженностью и является силовой характеристикой электростатического поля. Н.э.п в данной точке есть физическая величина, определяемой силой, действующей на пробный единичный заряд, помещенный в эту точку поля: E=F/Q0. С законом Кулона: E=1Qr/4πε0r2r или E=1Q/4πε0r2. Направление вектора E совпадает с направлением силы, действующей на положительный заряд. Если заряд +, то Е направлен вдоль радиус-вектора от заряда (отталкивание заряда); если -, то Е к заряду (притягивание). 1Н/м (В/м) – напряженность такого поля, которое на точечный заряд 1Кл действует с силой в 1Н. Графически электростатическое поле изображают с помощью линий напряженности - линий, касательные к которым в каждой точке совпадают с направлением вектора Е. Линии напряженности совпадают по направлению с вектором напряженности. Линии напряженности никогда не пересекаются. Для однородного поля (когда вектор напряженности в любой точке постоянен по величине и направлению) линии параллельны вектору. Если поле создается точечным зарядом, то линии напряженности – радиальные прямые, выходящие из заряда, если он +, и входящие в, если -. Для того, что бы с помощью линий напряженности можно было характеризовать не только направление, но и значение напряженности: EdScosα=EndS, En-проекция вектора Е на нормаль n к площади dS. Величина dФE=EndS=EdS называется потоком вектора напряженности через площадку dS [B·м]. Принцип независимости действия сил (как в механике) т.е. результирующая сила F, действующая со стороны поля на пробный заряд Q0, равна векторной сумме сил Fi, приложенных к нему со стороны каждого из зарядов Qi: F=ΣFi. F=Q0E и Fi=Q0Ei, где Е – напряженность результирующего поля, а Ei – напряженность поля, создаваемого зарядом Qi. E=ΣEi. Принцип суперпозиции (наложения) электростатических полей – напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.
Билет 2.2. Всякий реальный контур обладает активным сопротивлением. Энергия, запасенная в контуре, постепенно расходуется на нагревание этого сопротивления, вследствие чего свободные колебания затухают. Уравнение
К
 ирхгофа
для этого контура:
ирхгофа
для этого контура: 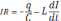 .
Разделим на L
и произведем замены:
Получим:
.
Разделим на L
и произведем замены:
Получим:
 .
Обозначим
.
Обозначим
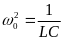 ,
а
,
а
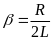 .
Тогда это уравнение запишется так:
.
Тогда это уравнение запишется так:
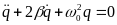 .
Решением этого уравнения является
функция
.
Решением этого уравнения является
функция
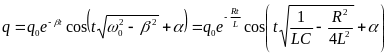 .
Напряжение на обкладках конденсатора
.
Напряжение на обкладках конденсатора
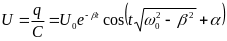 .
Сила тока в контуре
.
Сила тока в контуре
 Затухание
колебаний характеризуется логарифмическим
декрементом затухания:
Затухание
колебаний характеризуется логарифмическим
декрементом затухания:
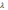 =
= ,
, 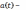 амплитуда соответствующей величины(q,
U,
I).
амплитуда соответствующей величины(q,
U,
I).
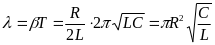 .
.
=1/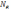 ,
-
число колебаний, совершаемых за время,
в течение которого амплитуда уменьшается
в е раз. Часто колебательный контур
характеризуется добротностью:
,
-
число колебаний, совершаемых за время,
в течение которого амплитуда уменьшается
в е раз. Часто колебательный контур
характеризуется добротностью:
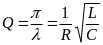 .
.
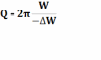 , W-
энергия, запасенная в системе в данный
момент;
, W-
энергия, запасенная в системе в данный
момент; 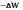 –убыль этой энергии за один период
колебаний. (Верно и для механической
системы). При
–убыль этой энергии за один период
колебаний. (Верно и для механической
системы). При
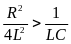 вместо колебаний происходит апериодический
разряд конденсатора. Сопротивление
контур, при котором колебательный
процесс переходит в апериодический,
называется критическим:
вместо колебаний происходит апериодический
разряд конденсатора. Сопротивление
контур, при котором колебательный
процесс переходит в апериодический,
называется критическим: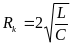 .
.
Б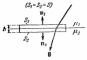
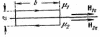 илет
3. Поток вектора напряженности. Теорема
Гаусса для вестора напряженности
электрического поля.
Линии напряженности условились проводить
с опр густотой: число линий напряженности,
пронизывающих единицу площади поверхности,
перпендикулярную линиям напряженности,
должно быть равно модулю вектора E.
Тогда число линий напряженности равно
EdScosα=EndS
(n
–нормаль, образующая с Е угол α). En-
проекция вектора Е на нормаль n
к площади dS.
Величина dФE=EndS=EdS
называется потоком вектора напряженности
через площадку dS=dSn
– вектор, модуль которого равен dS,
а направление совпадает с направлением
нормали n
к площадке. Единица потока вектора
напряженности электростатического
поля – 1 В·м. Для произвольной замкнутой
поверхности S
поток вектора E
сквозь эту поверхность ФE=s∫EndS=s∫EdS.
Поток вектора Е зависит не только от
поля Е, но и от выбора направления n.
Для замкнутых положительное направление
нормали – наружу. Поток вектора
напряженности сквозь сферическую
поверхность r,
охватывающей точечный заряд Q,
равен: ФE=s∫EndS=Q4πr2/4πε0r2=Q/ε0.
Справедливо для всех замкнутых
поверхностей. Вход линий напряженности
-, выход +. Знак потока совпадает со знаком
заряда. Теорема Гаусса: поток вектора
напряженности электростатического
поля в вакууме сквозь произвольную
замкнутую поверхность равен алгебраической
сумме заключенных внутри этой поверхности
зарядов, деленной на ε0.
Рассмотрим общий случай произвольной
поверхности, окружающей n
зарядов. По принципу суперпозиции E=ΣEi.
Поэтому ФE=
s∫EdS=
s∫(
ΣEi)dS=
Σ s∫EidS.
Каждый из интегралов равен Qi/ε0.
Следовательно, s∫EdS=
s∫EndS=1/ε0ΣQi.
Заряд может быть распределен с некоторой
объемной плотностью ρ=dQ/dV,
различной в разных местах. Тогда суммарный
заряд ΣQi=v∫ρdV.
Используя теорему Гаусса: s∫EdS=
s∫EndS=1/ε0v∫ρdV.
илет
3. Поток вектора напряженности. Теорема
Гаусса для вестора напряженности
электрического поля.
Линии напряженности условились проводить
с опр густотой: число линий напряженности,
пронизывающих единицу площади поверхности,
перпендикулярную линиям напряженности,
должно быть равно модулю вектора E.
Тогда число линий напряженности равно
EdScosα=EndS
(n
–нормаль, образующая с Е угол α). En-
проекция вектора Е на нормаль n
к площади dS.
Величина dФE=EndS=EdS
называется потоком вектора напряженности
через площадку dS=dSn
– вектор, модуль которого равен dS,
а направление совпадает с направлением
нормали n
к площадке. Единица потока вектора
напряженности электростатического
поля – 1 В·м. Для произвольной замкнутой
поверхности S
поток вектора E
сквозь эту поверхность ФE=s∫EndS=s∫EdS.
Поток вектора Е зависит не только от
поля Е, но и от выбора направления n.
Для замкнутых положительное направление
нормали – наружу. Поток вектора
напряженности сквозь сферическую
поверхность r,
охватывающей точечный заряд Q,
равен: ФE=s∫EndS=Q4πr2/4πε0r2=Q/ε0.
Справедливо для всех замкнутых
поверхностей. Вход линий напряженности
-, выход +. Знак потока совпадает со знаком
заряда. Теорема Гаусса: поток вектора
напряженности электростатического
поля в вакууме сквозь произвольную
замкнутую поверхность равен алгебраической
сумме заключенных внутри этой поверхности
зарядов, деленной на ε0.
Рассмотрим общий случай произвольной
поверхности, окружающей n
зарядов. По принципу суперпозиции E=ΣEi.
Поэтому ФE=
s∫EdS=
s∫(
ΣEi)dS=
Σ s∫EidS.
Каждый из интегралов равен Qi/ε0.
Следовательно, s∫EdS=
s∫EndS=1/ε0ΣQi.
Заряд может быть распределен с некоторой
объемной плотностью ρ=dQ/dV,
различной в разных местах. Тогда суммарный
заряд ΣQi=v∫ρdV.
Используя теорему Гаусса: s∫EdS=
s∫EndS=1/ε0v∫ρdV.
Билет 3.2. Условия на границе двух магнетиков.
Магнетики
– вещества, проявляющие магнитные
свойства в магнитном поле. Вблизи
поверхности раздела двух магнетиков
в. должны удовлетворять определенным
граничным условиям, которые вытекают
из соотношений: 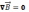 ,
,  . Возьмем на границе двух магнетиков с
проницаемостями
. Возьмем на границе двух магнетиков с
проницаемостями 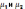 воображаемую цилиндрическую поверхность
высоты h
с основаниями S1
и S2
.
воображаемую цилиндрическую поверхность
высоты h
с основаниями S1
и S2
.
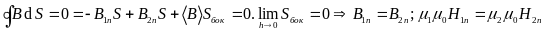 Рассмотрим теперь прямоугольный контур.
Вычислим для него циркуляцию
Рассмотрим теперь прямоугольный контур.
Вычислим для него циркуляцию 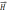 .
.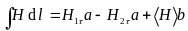 ,
где a
– сторона контура, параллельная границе
раздела, b
– перпендикулярная ей, а
,
где a
– сторона контура, параллельная границе
раздела, b
– перпендикулярная ей, а  -
среднее значение Н на участках b.
-
среднее значение Н на участках b.

 .
Вывод: пре переходе через границу
раздела двух магнетиков, нормальная
составляющая
.
Вывод: пре переходе через границу
раздела двух магнетиков, нормальная
составляющая  и тангенциальная составляющая
изменяются непрерывно. Тангенциальная
составляющая и нормальная составляющая
претерпевают разрыв. Таким образом, при
переходе через границу двух сред
ведет себя аналогично
и тангенциальная составляющая
изменяются непрерывно. Тангенциальная
составляющая и нормальная составляющая
претерпевают разрыв. Таким образом, при
переходе через границу двух сред
ведет себя аналогично  ,
а
,
а  .
.
З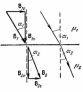 акон
преломления линий магнитной индукции.
акон
преломления линий магнитной индукции.
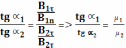
Б

 илет
4. Диполь. Поле диполя. Электрич.
диполем
наз. система двух одинаковых по величине
разноименных точечных зарядов +q
и –q,
расстояние l
между которыми значительно меньше
расстояния до тех точек, в которых
определяется поле системы. Прямая,
проходящая через оба заряда, наз. осью
диполя. Момент, действующий на диполь
в однородном поле
илет
4. Диполь. Поле диполя. Электрич.
диполем
наз. система двух одинаковых по величине
разноименных точечных зарядов +q
и –q,
расстояние l
между которыми значительно меньше
расстояния до тех точек, в которых
определяется поле системы. Прямая,
проходящая через оба заряда, наз. осью
диполя. Момент, действующий на диполь
в однородном поле

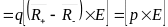 .Сила,
действующая на диполь в неоднородном
поле:
.Сила,
действующая на диполь в неоднородном
поле:
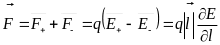 В
случае, если неоднородное поле симметрично
относительно оси x,
то сила
В
случае, если неоднородное поле симметрично
относительно оси x,
то сила
 ,
где
– угол наклона диполя к оси; его энергия
,
где
– угол наклона диполя к оси; его энергия
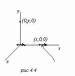
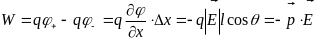 .Поле
диполя:Пусть дипольный момент, вектор
.Поле
диполя:Пусть дипольный момент, вектор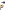 , в начале координат ориентирован вдоль
оси ОХ,
, в начале координат ориентирован вдоль
оси ОХ,
 . Вычислим поле в точке (х,0,0).
. Вычислим поле в точке (х,0,0).
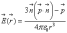
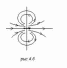 при
при
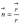 .Тогда
.Тогда
 .
На оси ОХ напряжённость поля убывает
как , то есть она обратно пропорциональна
кубу расстояния, от точечного заряда –
обратно пропорциональна квадрату
расстояния. Направление вектора
.
На оси ОХ напряжённость поля убывает
как , то есть она обратно пропорциональна
кубу расстояния, от точечного заряда –
обратно пропорциональна квадрату
расстояния. Направление вектора 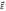 в точке (х,0,0) задаётся направлением
вектора
в точке (х,0,0) задаётся направлением
вектора 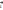 ,
то есть напряжённость направлен вдоль
оси ОХ. Теперь возьмём точку (0,у,0).
,
то есть напряжённость направлен вдоль
оси ОХ. Теперь возьмём точку (0,у,0).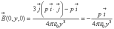 . Это означает, что для этого диполя
вектор
в точке (х,0,0) такой, а здесь в точке
(0,у,0) вектор
и по величине в два раза меньше, на том
же самом расстоянии, х=у. Электрический
диполь, ориентированный таким образом,
создаёт поле с такими силовыми линиями:
. Это означает, что для этого диполя
вектор
в точке (х,0,0) такой, а здесь в точке
(0,у,0) вектор
и по величине в два раза меньше, на том
же самом расстоянии, х=у. Электрический
диполь, ориентированный таким образом,
создаёт поле с такими силовыми линиями:
Вот такую структуру имеет поле диполя.
Взаимодействие токов. Закон Ампера.
Опыт
показывает, что электрические токи
взаимодействуют между собой. Сила
взаимодействия, приходящаяся на единицу
длины каждого из параллельных проводников,
пропорциональна величинам токов в них
и обратно пропорциональна расстоянию
между ними: 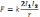
Ампер – сила тока, которая проходя по двум параллельным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1м друг от друга в вакууме, вызвал бы между этими проводниками силу, равную 2*10-7Н на каждый метр длины. Кулон – заряд, проходящий за 1с через поперечное сечение проводника, по которому течет постоянный ток силой 1А. Кл=А*с
В
рационализированном виде ,
,
 -
магнитная постоянная.
-
магнитная постоянная.  *10-6Гн/м
*10-6Гн/м
Каждый
носитель тока испытывает действие
магнитной силы. Действие этой силы
передается проводнику, по которому
заряды движутся. В результате магнитное
поле действует с определенной силой на
сам проводник с током. Выделим мысленно
элемент объема dV
проводника. В нем находится заряд-
носитель тока, равный  dV.
Тогда сила,действующая на элемент dV
проводника, может быть записана в виде:
dV.
Тогда сила,действующая на элемент dV
проводника, может быть записана в виде:
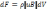 .
Так как j=
.
Так как j=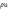 ,то
=|jB|dV.
Если ток течет по тонкому проводнику,
то jdV=Idl
и dF=I|dl,B|,
где dl-вектор,
совпадающие по направлению с током и
характеризующий элемент длины тонкого
проводника. Приведенные формулы выражают
Закон Ампера. Интегрируя эти выражения
по элементам тока(объемным или линейным),
можно найти магнитную силу, действующую
на тот или иной объем проводника или
его линейный участок.
,то
=|jB|dV.
Если ток течет по тонкому проводнику,
то jdV=Idl
и dF=I|dl,B|,
где dl-вектор,
совпадающие по направлению с током и
характеризующий элемент длины тонкого
проводника. Приведенные формулы выражают
Закон Ампера. Интегрируя эти выражения
по элементам тока(объемным или линейным),
можно найти магнитную силу, действующую
на тот или иной объем проводника или
его линейный участок.
Билет 5. Вектор электрического смещения. Теорема Гаусса для вектора электрического смещения.
Запишем
теорему Гаусса сторонних и связанных
электрических зарядов(т.к.они все
являются источниками поля Е) через поток
вектора Р 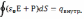 ,где
,где 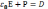 ,D-
вспомогательный вектор, поток которого
сквозь произвольную замкнутую поверхность
равен алгебраической сумме сторонних
зарядов, охватываемых этой поверхностью.
– это теорема Гаусса для поля вектора
D.
Данные соотношения справедливы для
любого диэлектрика, как изотропного,
так и анизотропного. Размерность D,
такая же как и вектора Р, единицей
величины D
служит кулон на квадратный метр(Кл/м2)
,D-
вспомогательный вектор, поток которого
сквозь произвольную замкнутую поверхность
равен алгебраической сумме сторонних
зарядов, охватываемых этой поверхностью.
– это теорема Гаусса для поля вектора
D.
Данные соотношения справедливы для
любого диэлектрика, как изотропного,
так и анизотропного. Размерность D,
такая же как и вектора Р, единицей
величины D
служит кулон на квадратный метр(Кл/м2)
Разветвление
цепи. Правила Кирхгофа. 1е
правило Кирхгофа: алгебраическая сумма
токов, сходящихся в узле равна нулю,
т.е. 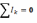 (1),
при этом токи, идущие к узлу, и токи,
исходящие из узла, величины разных
знаков. 1 закон Кирхгофа можно записать
для каждого из N
узлов цепи. Однако независимыми будут
только N-1
уравнений, N-е
– следствие из них.2е правило Кирхгофа:
(относится к любому выделенному в
разветвленной цепи замкнутому контуру)
алгебраическая сумма произведений сил
токов в отдельных участках произвольного
замкнутого контура на их сопротивления
равна алгебраической сумме ЭДС,
действующих в этом контуре.
(1),
при этом токи, идущие к узлу, и токи,
исходящие из узла, величины разных
знаков. 1 закон Кирхгофа можно записать
для каждого из N
узлов цепи. Однако независимыми будут
только N-1
уравнений, N-е
– следствие из них.2е правило Кирхгофа:
(относится к любому выделенному в
разветвленной цепи замкнутому контуру)
алгебраическая сумма произведений сил
токов в отдельных участках произвольного
замкнутого контура на их сопротивления
равна алгебраической сумме ЭДС,
действующих в этом контуре.  (2).
В разветвленной цепи независимыми будут
только уравнения для тех контуров,
которые нельзя получить наложением
других контуров друг на друга. При
составлении уравнений необходимо: 1)
обозначить стрелками предположительные
направления токов, в произвольном
направлении.2)выбрав произвольно
замкнутый контур, все его участки обойти
в одном направлении (например, по часовой
стрелке)если предположительное
направление обхода совпадает с выбранным,
то соответствующее слагаемое IR
в уравнение (2) надо брать со значением
+, если направления противоположны со
знаком -.аналогично поступается и с ЭДС.
Если какая-то ЭДС повышает потенциал в
направлении обхода, ее надо брать со
знаком +, иначе со знаком «-».
(2).
В разветвленной цепи независимыми будут
только уравнения для тех контуров,
которые нельзя получить наложением
других контуров друг на друга. При
составлении уравнений необходимо: 1)
обозначить стрелками предположительные
направления токов, в произвольном
направлении.2)выбрав произвольно
замкнутый контур, все его участки обойти
в одном направлении (например, по часовой
стрелке)если предположительное
направление обхода совпадает с выбранным,
то соответствующее слагаемое IR
в уравнение (2) надо брать со значением
+, если направления противоположны со
знаком -.аналогично поступается и с ЭДС.
Если какая-то ЭДС повышает потенциал в
направлении обхода, ее надо брать со
знаком +, иначе со знаком «-».
Билет 6.1.
Энергия электрического поля
П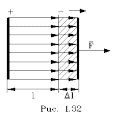 оле,
как и всякая физическая система, обладает
энеpгией. Энеpгия есть функция состояния,
а состояние поля определяется
напpяженностью. Следовательно, энеpгия
поля есть функция напpяженности. Однако
в случае неодноpодного поля напpяженность
поля в pазных его местах pазлична. Потому
необходимо ввести пpедставление о
концентpации энеpгии в поле, котоpая
меняется от точки к точке с изменением
напpяженности. Меpой концентpации энеpгии
поля служит ее плотность, котоpая
опpеделяется следующим обpазом.
оле,
как и всякая физическая система, обладает
энеpгией. Энеpгия есть функция состояния,
а состояние поля определяется
напpяженностью. Следовательно, энеpгия
поля есть функция напpяженности. Однако
в случае неодноpодного поля напpяженность
поля в pазных его местах pазлична. Потому
необходимо ввести пpедставление о
концентpации энеpгии в поле, котоpая
меняется от точки к точке с изменением
напpяженности. Меpой концентpации энеpгии
поля служит ее плотность, котоpая
опpеделяется следующим обpазом.
Рассмотpим некотоpый малый объем поля dV вблизи данной точки. Обозначим энеpгию поля в этом объеме чеpез dW. Под плотностью энеpгии поля в данной точке понимается отношение энеpгии dW к объему dV, то есть
п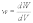 лотностью
энеpгии поля называется энеpгия поля,
пpиходящаяся на единицу объема вблизи
той точки, в котоpой эта плотность
опpеделяется: (1.61)
лотностью
энеpгии поля называется энеpгия поля,
пpиходящаяся на единицу объема вблизи
той точки, в котоpой эта плотность
опpеделяется: (1.61)
Плотность энеpгии поля - функция напpяженности поля в данном месте. Эту функцию тpебуется установить.
Рассмотpим поле плоского конденсатоpа. Это поле удобно тем, что оно одноpодно и плотность его энеpгии во всех точках одинакова.
Д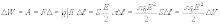 опустим,
что одна из пластин конденсатоpа
отодвигается на расстояние Dl (pис. 1.32).
Так как пластины заpяжены pазноименно
и пpитягиваются дpуг к дpугу, то пpи
pаздвигании пластин необходимо пpиложить
силу, pавную силе их пpитяжения, и совеpшить
pаботу. Кpоме того, пpи pаздвигании пластин
объем поля увеличивается (заштpихованная
часть поля на рисунке). Поэтому pабота
будет затpачена на увеличение энеpгии
поля конденсатоpа. Найдем это увеличение
энеpгии:
опустим,
что одна из пластин конденсатоpа
отодвигается на расстояние Dl (pис. 1.32).
Так как пластины заpяжены pазноименно
и пpитягиваются дpуг к дpугу, то пpи
pаздвигании пластин необходимо пpиложить
силу, pавную силе их пpитяжения, и совеpшить
pаботу. Кpоме того, пpи pаздвигании пластин
объем поля увеличивается (заштpихованная
часть поля на рисунке). Поэтому pабота
будет затpачена на увеличение энеpгии
поля конденсатоpа. Найдем это увеличение
энеpгии:
Как
в Савельеве:  . Энергия
равна интегралу от dW.
. Энергия
равна интегралу от dW.
Здесь под Е' нужно понимать напpяженность поля только положительно заpяженной пластины, котоpая pавна Е/2 (Е - напpяженность всего поля в конденсатоpе). Собственное поле заpяда, на котоpый действует электpо-статическая сила, учитывать не нужно. Таким обpазом, плотность энеpгии
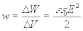
Плотность энеpгии электрического поля пpопоpциональна квадpату наpяженности.
Эта фоpмула, хотя и получена для одноpодного поля, веpна для любого электpического поля.
И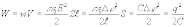 ногда
полезно знать энеpгию всего поля
конденсатоpа. Найдем для нее соответствующие
фоpмулы. Поле конденсатоpа одноpодно, а
поэтому вся энеpгия поля находится путем
умножения плотности энеpгии на объем
поля:
ногда
полезно знать энеpгию всего поля
конденсатоpа. Найдем для нее соответствующие
фоpмулы. Поле конденсатоpа одноpодно, а
поэтому вся энеpгия поля находится путем
умножения плотности энеpгии на объем
поля:
 -в
савельеве так! Везде U
вместо дельта фи
-в
савельеве так! Везде U
вместо дельта фи
Итак,
энеpгия поля плоского конденсатоpа может
быть пpедставлена либо фоpмулой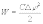
либо
фоpмулой

Фоpмулой (1.66) удобно пользоваться в случае если источник напpяжения отключен от конденсатоpа и q = const, а фоpмулой (1.65) - в случае если источник напpяжения подключен к конденсатоpу и Dj = const
