4. Проекция вектора на ось. Свойства проекции. Скалярное произведение. Выражение через проекцию. Свойства скалярного произведения. Условие ортогональности векторов.

Пусть в пространстве задана ось l, т. е. направленная прямая.

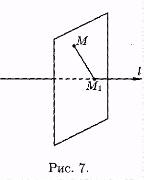
Проекцией точки М на ось l называется основание М₁ перпендикуляра ММ₁, опущенного из точки на ось.

Точка М₁ есть точка пересечения оси l с плоскостью, проходящей через точку М перпендикулярно оси (см. рис. 7).

Если точка М лежит на оси l, то проекция точки М на ось совпадает с М1.

Пусть АВ — произвольный вектор (АВ 0). Обозначим через А₁ и b ₁проекции на ось l соответственно начала А и конца В вектора АВ и рассмотрим вектор А₁В₁

Проекцией вектора АВ на ось l называет ся положительное число |A ₁B ₁ | , если вектор А ₁В ₁ и ось l одинаково направлены и отрица тельное число — |A ₁B ₁ | , если вектор А ₁В₁ и ось l противоположно направлены (см. рис. 8). Если точки a₁и b ₁совпадают (А ₁В ₁ =0), то проекция вектора АВ равна 0.

Проекция вектора АВ на ось l обозначается так: пр_lАВ. Если АВ=0 или АВl , то пр_l АВ=0.

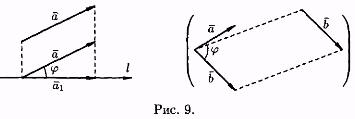
Угол   между вектором а и осью l (или угол между двумя векторами) изображен на рисунке 9. Очевидно,

Рассмотрим некоторые основные свойства проекций.

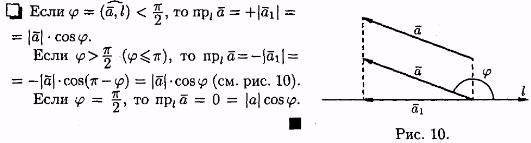
Свойство 1. Проекция вектора a на ось l равна произведению модуля вектора a на косинус угла   между вектором и осью, т. е. пр_la =|a |•cos  .

Следствие 5.1. Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол — прямой.

Следствие 5.2. Проекции равных векторов на одну и ту же ось равны между собой.

Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.

Скалярное произведение векторов  ,   обозначается символом   (порядок записи сомножителей безразличен, то есть  ).

Если угол между векторами  ,   обозначить через  , то их скалярное произведение можно выразить формулой

 (1)

Скалярное произведение векторов  ,   можно выразить также формулой

, или  .

Из формулы (1) следует, что  , если   - острый угол,  , если   - тупой угол;   в том и только в том случае, когда векторы   и   перпендикулярны (в частности,  , если   или  ).

Скалярное произведение   называется скалярным квадратом вектора и обозначается символом  . Из формулы (1) следует, что скалярный квадрат вектора равен квадрату его модуля:

.

Если векторы   и   заданы своими координатами:

,  ,

то их скалярное произведение может быть вычислено по формуле

.

Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов

.

Угол   между векторами

,  ,

дается формулой 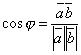 , или в координатах

.

Проекция произвольного вектора   на какую-нибудь ось u определяется формулой

,

где   - единичный вектор, направленный по оси u. Если даны углы  ,  ,  , которые оси u составляет с координатными осями, то   и для вычисления вектора   может служить формула

.

  Свойства векторного произведения:            если  , то   равен площади параллелограмма, построенного на приведенных к общему началу векторах   и  .

Два вектора называют ортогональными, если их скалярное произведение равно нулю.