5. Левые и правые тройки векторов. Векторное произведение. Свойства.

Векторным произведением вектора   на вектор   называется вектор, обозначаемый символом   и определяемый следующими тремя условиями:

1). Модуль вектора   равен  , где   - угол между векторами   и  ;

2). Вектор   перпендикулярен к каждому из вектора   и  ;

3). Направление вектора   соответствует «правилу правой руки». Это означает, что если векторы  ,   и   приведены к общему началу, то вектор   должен быть направлен так, как направлен средний палец правой руки, больой палец которой направлен по первому сомножителю (то есть по вектору  ), а указательный - по второму (то есть по вектору  ).

Векторное произведение зависит от порядка сомножителей, именно:

.

Модуль векторного произведения   равен площади S параллелограмма, построенного на векторах   и  :

.

Само векторное произведение может быть выражено формулой

,

где   - орт векторного произведения.

Векторное произведение   обращается в нуль тогда и только тогда, когда векторы   и   коллинеарны. В частности,  .

Если система координатных осей правая и векторы   и   заданы в этой системе своими координатами:

,  ,

то векторное произведение вектора   на вектор   определяется формулой

,

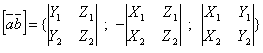или

.

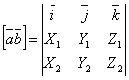Алгебраические свойства векторного произведения

Представление	Описание
	свойство антикоммутативности
	свойство ассоциативности относительно умножения на скаляр
	свойство дистрибутивности по сложению
	тождество Якоби, выполняется в   и нарушается в
	формула «БАЦ минус ЦАБ», тождество Лагранжа
	Это частный случай мультипликативности   нормы кватернионов
	значение этого выражения называют смешанным произведением векторов a, b, c и обозначают   либо

6. Смешанное произведение. Свойства. Условие компланарности векторов.

Сме́шанное произведе́ние   векторов   — скалярное произведение вектора   на векторное произведение векторов   и  :

.

Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).

Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами  .

Смешанное произведение кососимметрично по отношению ко всем своим аргументам:

т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что

Смешанное произведение   в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов   и  :

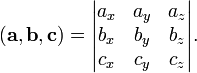
Смешанное произведение   в левой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов   и  , взятому со знаком "минус":

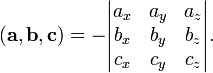
В частности,

Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.

Геометрический смысл — Смешанное произведение   по абсолютному значению равно объёму параллелепипеда (см. рисунок), образованного векторами   и  ; знак зависит от того, является ли эта тройка векторов правой или левой.

Смешанное произведение компланарных векторов  .