Вопрос 14

Понятие непрерывности функции.

Введем разности ∆x=x-x₀ и ∆f(x₀)=f(x₀)- f(x), которые будем называть соответственно приращениями аргумента и функции в точке x₀.Ясно,что f(x) непрерывна в точке x₀ тогда и только тогда, когда разность ∆f(x₀)→0 при ∆x₀ →0. Это дает нам возможность дать такое определение непрерывности: Функция f(x) непрерывна в точке x₀ , если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Функция f непрерывна на множестве E, если она непрерывна в каждой точке данного множества.

1.Теорема Если функции f(x) и g(x) непрерывны в точке x_0, то в этой точке непрерывны f(x)±g(x), f(x)g(x) и , если g(x)≠0. Док-во. Это теорема является частным случаем о пределах суммы, разности, произведения и частного. Действительно, непрерывность f(x) и g(x) в точке x₀ означает, что f(x) → f(x₀) и g(x)→ g(x₀ ) при x→x₀ . Тогда f(x)±g(x)→ f(x₀)±g(x₀),f(x)g(x) и , если g(x₀) ≠0. Тем самым, теорема доказана.

2.Теорема о непрерывности сложных функций.

Пусть y=f(x), y₀ =f(x₀), z=g(y), z₀ =g(y₀). Тогда если f(x) непрерывна в точке x₀ , а g(y) непрерывна в точке y₀ , то сложная функция g(f(x)) непрерывна в точке x₀ , то есть суперпозиция непрерывных функций непрерывна. Док-во. Возьмем x₀ и найдем y₀ , по которому получим z₀ . Дадим x₀ некоторое приращение ∆x₀ . Оно вызовет приращение ∆y₀ , которое в свою очередь, породит приращение ∆z₀ . Если ∆x₀ →0, то ∆y₀ →0 из-за непрерывности функции f. Но при ∆y₀ →0 ,будет ∆z₀ →0, так как непрерывна функция g. Таким образом, оказывается ∆z₀ →0 при ∆x₀ →0. Значит, суперпозиция непрерывна. Теорема доказана.

Точки разрыва/ Если попытаться построить отрицание свойства непрерывности функции в точке (предельной для области определения), то получится следующее. Существует такая окрестность значения функции в рассматриваемой точке, что сколь близко мы не подходили бы к данной точке, всегда можно будет найти точку, значение в которой окажется за пределами заданной окрестности.

В этом случае говорят, что функция f терпит разрыв в точке a.

Точкой разрыва функции f(x) называют такую точку х₀, в которой нарушается правило

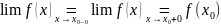
1)Оба предела существуют и равны, но не равны f(x₀) ,то есть f(x₀ – 0) = f(x₀ + 0) ≠ f(x₀). В этом случае точку x₀ называют устранимой точкой разрыва Действительно, если мы доопределим f , положив f(x₀) = f(x₀ – 0) = f(x₀ + 0), то она станет непрерывной

2)Оба предела существуют, но они не равны, то есть f(x₀ – 0) ≠ f(x₀ + 0). В этом случае точку x₀ называют точкой разрыва первого рода. Заметим, что в этом случае значение f(x₀) нас не интересует.

Разность f(x₀ – 0) - f(x₀ + 0) называется скачком функции f в точке разрыва. Пример. 1(х)= Очевидно, что 1(+0) = 1,

1(-0),то есть x₀ = 0 является точкой разрыва первого рода, причём скачок функции в этой точке равен 1. Эту функцию называют единичной функцией, или функцией единичного скачка.

Все остальные точки разрыва называются точками разрыва второго рода. Ясно, что в точке разрыва второго рода хотя бы один из пределов f(x₀ – 0) и f(x₀ + 0) не существует.