
Вопрос 11
Как известно, сумма, разность и произведение двух б.м.ф. есть функция б.м. Отношение двух б.м.ф. есть функция б.м. Отношение же двух б.м.ф. может вести себя различным образом: быть конечным числом, быть бесконечно большой функцией, бесконечно малой или вообще не стремиться ни к какому пределу. Две б.м.ф. сравниваются между собой с помощью их отношения. Пусть α=α(х) и β=β(х) есть б.м.ф. при х->x0, т.е. lim α(x)=0(x->x0) и limβ(x)=0(x->x0)
1.Если lim (α/β)=A=!0, то α и β называются б.м. одного порядка малости
2.Если lim (α/β)=A=0, то α называется б.м. более высокого порядка малости, чем β
3.Если lim (α/β)=A=∞, то α называется б.м. более низкого порядка малости, чем β
4.Если lim (α/β) не существует, то α и β называются несравнимыми.
Теорема. Предел отношения двух б.м. функций не изменится, если каждую или одну из них заменить эквивалентной ей б.м. Пусть α~α` и β~β` при х->x0. Тогда lim(α/β)= lim((α/β)*(α`/α`)*(β`/β`))=lim(α/α`)* lim(β`/β)* lim(α`/β`), т.е. lim(α/β)= lim(α`/β`) (везде x->x0).
Вопрос 12
Т1. Разность двух эквивалентных б.м.ф. есть б.м. более высокого порядка, чем каждая из них.
Пусть α~β при х->х0. Тогда lim(1-(β/α)=1-lim(β/α)=1-1=0.
Т2.Сумма конечного числа б.м.ф. разных порядков малости эквивалентна слагаемому низшего порядка. Пусть α->0 и β->0 при х->x0, причем α – б.м.ф. высшег порядка, чем β, т.е. lim (α/β)=0 при x->x0. Тогда lim((α+β)/β)=lim(α/β+1)=lim(α/β) + 1=0+1=1 (везде x->x0). Следовательно (α+β)~β при x->x0. Слагаемое, эквивалентное сумме б.м.ф. , называется главной частью этой суммы. Замена суммы б.м.ф. называется отбрасыванием б.м. высшего порядка.
Вопрос 13
Понятие непрерывности функции.
Введем разности ∆x=x-x0 и ∆f(x0)=f(x0)- f(x), которые будем называть соответственно приращениями аргумента и функции в точке x0.Ясно,что f(x) непрерывна в точке x0 тогда и только тогда, когда разность ∆f(x0)→0 при ∆x0 →0. Это дает нам возможность дать такое определение непрерывности: Функция f(x) непрерывна в точке x0 , если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Функция f непрерывна на множестве E, если она непрерывна в каждой точке данного множества.
Точки разрыва/ Если попытаться построить отрицание свойства непрерывности функции в точке (предельной для области определения), то получится следующее. Существует такая окрестность значения функции в рассматриваемой точке, что сколь близко мы не подходили бы к данной точке, всегда можно будет найти точку, значение в которой окажется за пределами заданной окрестности.
В этом случае говорят, что функция f терпит разрыв в точке a.
Теорема
1./Если функции
f(x)
и g(x)
непрерывны в точке x0,
то в этой
точке непрерывны f(x)±g(x),
f(x)g(x)
и
 ,
если g(x)≠0.
,
если g(x)≠0.
Док-во.
Это теорема является частным случаем
о пределах суммы, разности, произведения
и частного. Действительно, непрерывность
f(x)
и g(x)
в точке x0
означает,
что f(x)
→ f(x0)
и g(x)→
g(x0
) при x→x0
. Тогда
f(x)±g(x)→
f(x0)±g(x0),f(x)g(x)
и
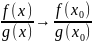 ,
если g(x0)
≠0. Тем самым, теорема доказана.
,
если g(x0)
≠0. Тем самым, теорема доказана.
