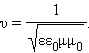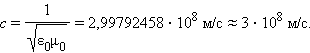- •Контур с током в магнитном поле
- •Работа перемещения проводника и контура с током в магнитном поле
- •Действие магнитного поля на движущиеся электрические заряды. Сила Лоренца.
- •Движение заряженных частиц в магнитном поле. Принцип действия циклических ускорителей.
- •Эффект Холла.
- •Вихревой характер магнитного поля.
- •Закон полного тока. Применение закона полного тока для расчета магнитного поля тороида.
- •Магнитный поток. Теорема гаусса для магнитных полей.
- •Законы магнитных цепей
- •Магнетики. Намагничивание магнетиков. Вектор намагничения.
- •Напряженность магнитного поля. Связь между векторами j,b,h.
- •Доменная структура ферромагнетиков. Магнитный гистерезис.
- •Явление электромагнитной индукции. Закон Фарадея и правило Ленца.
- •Электронный механизм возникновения эдс индукции.
- •Явление самоиндукции. Индуктивность, единицы её измерения. Индуктивность длинного соленоида.
- •????? Установление тока в цепи, содержащей катушку индуктивности.
- •Взаимная индукция. Коэффициент взаимной индукции.
- •Энергия системы проводников с токами?????. Энергия магнитного поля. Объемная плотность энергии магнитного поля.
- •Вихревое электрическое поле. Первое уравнение Максвела в интегральной форме.
- •Взаимосвязь электрического и магнитного полей. Ток смещения. Второе уравнение теории максвелла в интегральной форме.
- •Полная система уравнений Максвелла в дифференциальной форме.
- •Природа носителей тока в металлах. Доказательство электронной проводимости металлов.
- •Классическая теория проводимости металлов. Вывод законов Ома и Джоуля-Ленца из электронной теории.
- •Связь между электропроводностью и теплопроводностью. Закон Видемана-Франца.
- •Трудности классической электронной теории.
- •Гармонические колебания. Линейный гармонический осциллятор. Математический и физический маятники.
- •Решения уравнения движения
- •Сложение гармонических колебаний.
- •Затухающие и вынужденные колебания.
- •Свободные колебания в электрическом колебательном контуре.
- •Вынужденные колебания. Добротность колебательного контура. Переменный электрический ток.
- •Резонанс напряжений в электрической цепи.
- •Резонанс токов в электрической цепи.
- •Автоколебания. Понятие о релаксационных колебаниях.
- •Упругие волны(продольные, поперечные). Уравнение бегущей волны(плоской сферической).
- •Уравнение плоской волны
- •Уравнение сферической волны
- •Свойства электромагнитных волн. Плоские электромагнитные волны.
- •Эффект Доплера для акустических и световых волн.?????
- •Энергия и импульс электромагнитных волн. Вектор Пойтинга.
- •Дипольное излучение электромагнитных волн.?????
- •Световые волны. Абсолютный и относительный показатели преломления. Интенсивность света.
- •Принцип Ферма. Вывод законов отражения и преломления света.
- •Когерентные волны. Способы получения когерентных волн.
- •Интерференция световых волн. Когерентность.
- •Расчет интерференционной картины от двух когерентных источников.
- •Интерференция в тонких пленках. Полосы равной толщины и равного наклона.
Уравнение плоской волны
Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер.
Направим
оси координат так, чтобы ось x
совпадала с направлением распространения
волны. Тогда волновая поверхность будет
перпендикулярна оси x.
Так как все точки волновой поверхности
колеблются одинаково, смещение x будет
зависеть только от х
и t:
![]() .
Пусть колебание точек, лежащих в плоскости
.
Пусть колебание точек, лежащих в плоскости
![]() ,
имеет вид (при начальной фазе
,
имеет вид (при начальной фазе
![]() )
)
|
|
(5.2.2) |
|
Найдем
вид колебания частиц в плоскости,
соответствующей произвольному значению
x.
Чтобы пройти путь x,
необходимо время
![]() .
.
Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости , т.е.
|
|
(5.2.3) |
|
– это уравнение плоской волны.
Таким
образом, x есть
смещение
любой из точек с координатой x в момент
времени t.
При выводе мы предполагали, что амплитуда
колебания
![]() .
Это будет, если энергия волны не
поглощается средой.
.
Это будет, если энергия волны не
поглощается средой.
Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z.
В общем виде уравнение плоской волны записывается так:
|
|
(5.2.4) |
|
Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны.
Уравнение (5.2.3) описывает волну, распространяющуюся в сторону увеличения x. Волна, распространяющаяся в противоположном направлении, имеет вид:
![]() .
.
Уравнение волны можно записать и в другом виде.
Введем
волновое число
![]() ,
или в векторной форме:
,
или в векторной форме:
|
|
(5.2.5) |
|
где
![]() –
волновой вектор,
–
волновой вектор,
![]() –
нормаль к волновой поверхности.
–
нормаль к волновой поверхности.
Так
как
![]() ,
то
,
то
![]() .
Отсюда
.
Отсюда
![]() .
Тогда
уравнение плоской волны
запишется так:
.
Тогда
уравнение плоской волны
запишется так:
|
|
(5.2.6) |
|
Уравнение сферической волны
В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической.
Предположим,
что фаза
колебаний источника равна wt
(т.е.
![]() ).
Тогда точки, лежащие на волновой
поверхности
радиуса r,
будут иметь фазу
).
Тогда точки, лежащие на волновой
поверхности
радиуса r,
будут иметь фазу
![]() .
Амплитуда колебаний здесь, даже если
волна не поглощается средой, не будет
постоянной, она убывает по закону
.
Амплитуда колебаний здесь, даже если
волна не поглощается средой, не будет
постоянной, она убывает по закону
![]() .
Следовательно, уравнение
сферической волны:
.
Следовательно, уравнение
сферической волны:
|
|
(5.2.7) |
|
где А равна амплитуде на расстоянии от источника равном единице.
Уравнение
(5.2.7) неприменимо для малых r,
т.к. при
![]() ,
амплитуда стремится к бесконечности.
То, что амплитуда колебаний
,
амплитуда стремится к бесконечности.
То, что амплитуда колебаний
![]() ,
следует из рассмотрения энергии,
переносимой волной.
,
следует из рассмотрения энергии,
переносимой волной.
Свойства электромагнитных волн. Плоские электромагнитные волны.
Существование
электромагнитных волн было теоретически
предсказано великим английским физиком
Дж. Максвеллом в 1864 году. Максвелл
проанализировал все известные к тому
времени законы электродинамики и сделал
попытку применить их к изменяющимся во
времени электрическому и магнитному
полям. Он обратил внимание на ассиметрию
взаимосвязи между электрическими и
магнитными явлениями. Максвелл ввел в
физику понятие вихревого
электрического поля
и предложил новую трактовку закона
электромагнитной
индукции,
открытой Фарадеем в 1831 г.:Всякое
изменение магнитного поля порождает в
окружающем пространстве вихревое
электрическое поле, силовые линии
которого замкнуты.
Максвелл высказал гипотезу о существовании
и обратного процесса: Изменяющееся
во времени электрическое поле порождает
в окружающем пространстве магнитное
поле. Гипотеза
Максвелла была лишь теоретическим
предположением, не имеющим экспериментального
подтверждения, однако на ее основе
Максвеллу удалось записать непротиворечивую
систему уравнений, описывающих взаимные
превращения электрического и магнитного
полей, то есть систему уравнений
электромагнитного
поля (уравнений
Максвелла). Из теории Максвелла вытекает
ряд важных выводов: 1. Существуют
электромагнитные волны, то есть
распространяющееся в пространстве и
во времени электромагнитное поле.
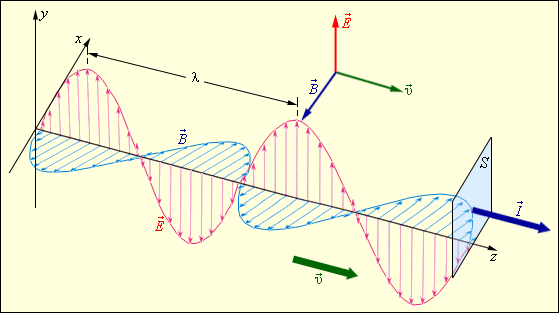
Электромагнитные волны поперечны
– векторы
![]() и
и
![]() перпендикулярны
друг другу и лежат в плоскости,
перпендикулярной направлению
распространения волны (рис. 5.6.3).
перпендикулярны
друг другу и лежат в плоскости,
перпендикулярной направлению
распространения волны (рис. 5.6.3).
|
2. Электромагнитные волны распространяются в веществе с конечной скоростью
|
Здесь ε и μ – диэлектрическая и магнитная проницаемости вещества, ε0 и μ0 – электрическая и магнитная постоянные: ε0 = 8,85419·10–12 Ф/м, μ0 = 1,25664·10–6 Гн/м. Скорость электромагнитных волн в вакууме (ε = μ = 1):
|
3. В электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры». Поэтому объемные плотности электрической и магнитной энергии равны друг другу: wэ = wм.
|
Отсюда следует, что в электромагнитной волне модули индукции магнитного поля и напряженности электрического поля в каждой точке пространства связаны соотношением
|
4. Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии. Если выделить площадку S (рис. 5.6.3), ориентированную перпендикулярно направлению распространения волны, то за малое время Δt через площадку протечет энергия ΔWэм, равная
ΔWэм = (wэ + wм)υSΔt. |
|
Волна
с постоянной амплитудой колебаний в
любой точке наблюдения называется
плоской
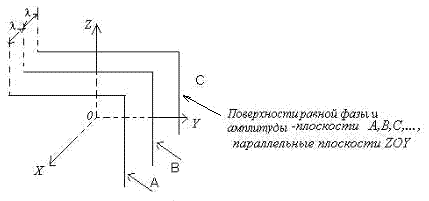
Наиболее
простое выражение для векторов
электромагнитного поля имеет плоская
волна, распространяющаяся вдоль одной
их координатных осей принятой декартовой
системы координат
![]() ,
например, вдоль оси
,
например, вдоль оси
![]() (рис.1.1).
Колебания вектора напряжённости
электрического поля такой волны будет
определяться выражением
(рис.1.1).
Колебания вектора напряжённости
электрического поля такой волны будет
определяться выражением
|
(1.3a) |
где
![]() 0
- амплитуда колебаний электрического
вектора, постоянная во всех точках
пространства; k x=((
0
- амплитуда колебаний электрического
вектора, постоянная во всех точках
пространства; k x=((![]() )
- пространственная составляющая полной
фазы волны, которая имеющая постоянное
значение в любой плоскости, параллельной
плоскости ZOY, определяемое расстоянием,
которое прошла волна от точки
)
- пространственная составляющая полной
фазы волны, которая имеющая постоянное
значение в любой плоскости, параллельной
плоскости ZOY, определяемое расстоянием,
которое прошла волна от точки
![]() -
начальная фаза колебаний волны при
-
начальная фаза колебаний волны при
![]() .
.
Колебания вектора напряжённости магнитного поля такой волны будет определяться аналогичным выражением
|
(1.3b) |
где
![]() -
амплитуда колебаний электрического
вектора, постоянная во всех точках
пространства.
-
амплитуда колебаний электрического
вектора, постоянная во всех точках
пространства.
.
|
Рис. 1.1. |