30. Затухающие и вынужденные колебания.

Затухающими называются колебания, энергия и амплитуда которых уменьшается с течением времени. Затухание свободных механических колебаний связано с убыванием механической энергии за счет действия сил сопротивления и трения.

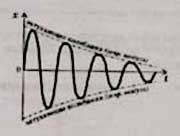ПРЕВРАЩЕНИЯ ЭНЕРГИИ ПРИ КОЛЕБАТЕЛЬНОМ ДВИЖЕНИИ

Колебания маятника возможны благодаря начальному запасу механической энергии, которая придается ему при выведении из положения равновесия. При колебаниях маятника: - в положении равновесия скорость и, следовательно, кинетическая энергия тела максимальны. - потенциальная энергия маятника максимальна, когда кинетическая энергия (скорость) равна нулю.

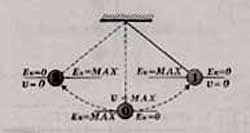
При движении маятника из положения равновесия в положение с максимальным смещением кинетическая энергия превращается в потенциальную энергию. При перемещении из положения с максимальным смещением в положение равновесия потенциальная энергия переходит в кинетическую.

Если колебания свободные, т.е. трение отсутствует, то выполняется закон сохранения механической энергии: сумма кинетической и потенциальной энергий остается неизменной.

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

Вынужденными колебаниями называются незатухающие колебания системы, которые вызываются действием внешней периодической силы.

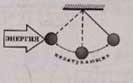Сила, вызывающая вынужденные колебания, называется вынуждающей или возмущающей силой.

31. Свободные колебания в электрическом колебательном контуре.

Всякий реальный колебательный контур обладает сопротивлением (рис.16.3). Энергия электрических колебаний в таком контуре постепенно расходуется на нагревание сопротивления, переходя в джоулево тепло, вследствие чего колебания затухают.

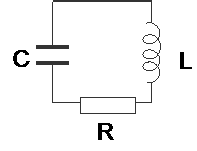
Рис.16.3. Колебательный RLC-контур.

Уравнение свободных затухающих колебаний можно получить, исходя из того, что в отсутствии внешнего источника напряжения, сумма падений напряжений на индуктивности, емкости и сопротивлении равна нулю для любого момента времени:

или, поскольку ,

.

Введя обозначение

,

этому уравнению можно придать вид:

,

где .

Решение полученного уравнения имеет вид:

где

Мы видим, что частота свободных затухающих колебаний ω^′ меньше собственной частоты ω₀. Подставив значения ω₀ и β, получим:

Амплитуда затухающих колебаний заряда конденсатора q₀(t) уменьшается со временем по экспоненциальному закону (рис.16.4). Коэффициент β называется коэффициентом затухания.

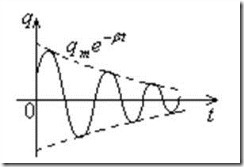
Рис.16.4. Изменение заряда конденсатора со временем в RLC-контуре.

Затухание колебаний принято характеризовать декрементом колебаний λ, определяемым как:

.Легко видеть, что декремент колебаний обратен по величине числу колебаний N_e, совершаемых за время, в течение которого амплитуда колебаний уменьшается в е раз: λ=1/N_e.

32. Вынужденные колебания. Добротность колебательного контура. Переменный электрический ток.

Добротностью колебательного контура называется величина:

Из этой формулы видно, что добротность тем выше, чем меньше коэффициент затухания β. При малых затуханиях (λ<<1) можно приближенно считать, что

.

Амплитуда тока в контуре, как и заряд на конденсаторе, убывает со временем по закону . Энергия W, запасенная в контуре, пропорциональна квадрату амплитуды тока (или квадрату напряжения на конденсаторе). Следовательно, W убывает со временем по закону e^-2βt. Относительное уменьшение энергии за период колебания Т (при малом затухании) есть:

.

Таким образом, потери энергии в колебательном контуре тем меньше, чем выше его добротность.

Если в цепь электрического контура, содержащего емкость, индуктивность и сопротивление, включить источник переменной ЭДС (рис.16.5), то в нем, наряду с собственными затухающими колебаниями, возникнут незатухающие вынужденные колебания. Частота этих колебаний совпадает с частотой изменения переменной ЭДС.

Рис.16.5. Последовательный колебательный RLC-контур.

Чтобы получить уравнение вынужденных колебаний, надо, согласно второму правилу Кирхгофа, приравнять сумму падений напряжений на элементах контура приложенной ЭДС:

или

где Е₀ - амплитуда переменной ЭДС; ω – ее циклическая частота.

Интересующее нас частное решение этого дифференциального уравнения имеет вид:

где

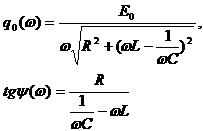
Решение соответствующего однородного уравнения, как мы видели в п.5.2, представляет собой свободные затухающие колебания, которые с течением времени становятся исчезающе малыми, и их можно в дальнейшем не учитывать.

Выпишем формулы для силы тока в цепи и падений напряжений на каждом из элементов контура.

Сила тока: ,

.

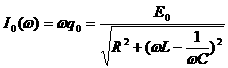По аналогии с законом Ома для полной цепи по постоянному току величину

называют полным сопротивлением цепи по переменному току. Эта величина представляет собой модуль комплексного сопротивления , называемого также импедансом цепи. Сопротивление R называют активным сопротивлением (на нем выделяется тепло). Чисто мнимые сопротивления ωL и называют соответственно индуктивным и емкостным реактивными сопротивлениями (на них тепло не выделяется).

Напряжение на сопротивлении R:

,

.

Напряжение на конденсаторе С:

,

.

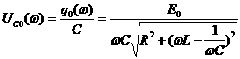Напряжение на катушке индуктивности L:

,

.

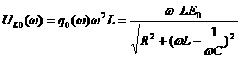Сравнивая написанные формулы, видим, что изменение напряжения на сопротивлении следует за изменением силы тока в цепи без отставания или опережения по фазе, изменение напряжение на конденсаторе отстает по фазе на , а на индуктивности опережает по фазе на изменение тока.

П.Т.Установившиеся вынужденные электромагнитные колебания можно исследовать как протекание в цепи, которая содержит резистор, катушку индуктивности и конденсатор, переменного тока. Переменный ток можно считать квазистационарным, т. е. для него мгновенные значения силы тока во всех сечениях цепи практически одинаковы, поскольку их изменения происходят достаточно медленно, а электромагнитные возмущения передаются по цепи со скоростью, которая равна скорости света. Для мгновенных значений квазистационарных токов выполняются закон Ома и слудующие из него правила Кирхгофа, которые будут применены к переменным токам. Рассмотрим последовательно процессы, которые происходят на участке цепи, содержащей резистор, катушку индуктивности и конденсатор, к концам которого приложено переменное напряжение (1) где U_m — амплитуда напряжения. 1. Переменный ток, текущий через резистор сопротивлением R (L→0, C→0) (рис. 1а). При выполнении условия квазистационарности ток через резистор находится через закон Ома: где амплитуда силы тока I_m= U_m/R. На рис. 1б показана векторная диаграмма амплитудных значений тока I_m и напряжения U_m на резисторе (сдвиг фаз между I_m и U_m равен нулю).

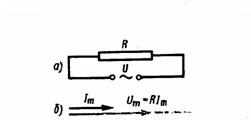
Рис.1

2. Переменный ток, текущий через катушку индуктивностью L (R→0, C→0) (рис. 214, а). Если в цепи действует переменное напряжение (1), то в ней идет переменный ток, в результате чего появляется э.д.с. самоиндукции ξ_s = -L(dI/dt) . Тогда закон Ома для данного участка цепи имеет вид откуда (2) Поскольку внешнее напряжение приложено к катушке индуктивности, то (3) равно падению напряжения на катушке. Из формулы (2) вытекает, что проинтегрировав, учтя при этом, что постоянная интегрирования равна нулю (поскольку отсутствует постоянная составляющая тока), найдем (4) где I_m= =U_m/(ωL). Величина (5) имеет название реактивное индуктивное сопротивление (или индуктивное сопротивление). Из формулы (5) следует, что для постоянного тока (ω = 0) катушка индуктивности не имеет сопротивления. Подстановка значения U_m = ωLI_m в формулу (2) с учетом (3) дает следующее значение падения напряжения на катушке индуктивности: (6) Сравнение формул (4) и (6) приводит к заключению, что падение напряжения U_L опережает по фазе ток I, который текет через катушку, на π/2, что и продемонстрировано на векторной диаграмме (рис. 2б).

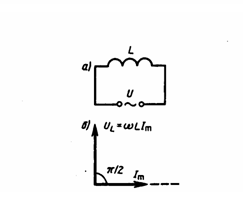
Рис.2

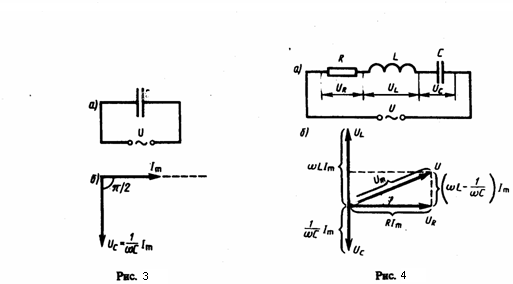
3. Переменный ток, текущий через конденсатор емкостью С (R→0, L→0) (рис. 3а). Если переменное напряжение (1) приложено к конденсатору, то он все время перезаряжается, и в цепи протекает переменный ток. Поскольку все внешнее напряжение приложено к конденсатору, и сопротивление подводящих проводов мы не учитываем, то Сила тока (7) где Величина называется реактивным емкостным сопротивлением (или емкостным сопротивлением). Для постоянного тока (ω=0) R_C = ∞ , т. е. постоянный ток через конденсатор течь не может. Падение напряжения на конденсаторе (8) Сравнение формул (7) и (8) приводит к заключению, что падение напряжения U_C отстает по фазе от тока I, текущего через конденсатор на π/2. Это продемонстрировано на векторной диаграмме (рис. 3б).

4. Цепь переменного тока, содержащая последовательно включенные резистор, катушку индуктивности и конденсатор. На рис. 4а показан участок цепи, который содержит резистор сопротивлением R, катушку индуктивностью L и конденсатор емкостью С, у которого к концам приложено переменное напряжение (1). В цепи появляется переменный ток, который приветдет к падению напряжения на всех элементах цепи соответственно равные U_R, U_L и U_C. На рис. 4б дана векторная диаграмма амплитуд падений напряжений на резисторе (U_R), катушке (U_L) и конденсаторе (U_C). Амплитуда U_m приложенного напряжения должна быть равна векторной сумме амплитуд этих падений напряжений. Как мы замечаем из рис. 4б, угол φ задает разность фаз между напряжением и силой тока. Из рисунка видно, что (9) Из прямоугольного треугольника находим откуда амплитуда силы тока равна (10) совпадающее с уравнением переменного тока для вынужденных электромагнитных колебаний (формула (15) этого раздела). Значит, если напряжение в цепи изменяется по закону U = U_mcosωt, то ток, текущий в цепи (11) где φ и I_m находятся соответственно из формул (9) и (10). Величина (12) имеет название полное сопротивление цепи, а величина - реактивное сопротивление. Исследуем частный случай, когда в цепи отсутствует конденсатор. В данном случае падения напряжений U_R и U_L в сумме равны приложенному напряжению U. Векторная диаграмма для данного случая дана на рис. 5, из которого видно, что (13) Выражения (9) и (10) тождественны (13), если в них 1/(ωC)=0, т.е. С=∞ . Значит, отсутствие конденсатора в цепи означает С=∞ , а не С=0. Данный вывод можно озвучить следующим образом: сближая обкладки конденсатора до их полного соприкосновения, получим цепь, в которой отсутствует конденсатор (расстояние между обкладками стремится к нулю, а емкость - к бесконечности.

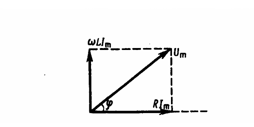
Рис.5