47. Экстремум функции многих переменных (необходимое и достаточное условия).
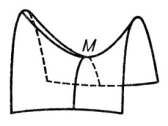
Экстремум (от лат. extremum - крайнее), значение непрерывной функции f (x), являющееся или максимумом, или минимумом. Точнее: непрерывная в точке х0 функция f (x) имеет в x0 максимум (минимум), если существует окрестность (x0 + d, x0 - d) этой точки, содержащаяся в области определения f (x), и такая, что во всех точках этой окрестности выполняется неравенство f (x0), ³ f (x) [соответственно, f (x0) £ f (x)]. Если при этом существует такая окрестность, что в ней f (x0) > f (x) [или f (x0) << f (x)] при х ¹ x0, то говорят о строгом, или собственном, максимуме (минимуме), в противном случае - о нестрогом, или несобственном, максимуме (минимуме) (на рис. 1 в точке А достигается строгий максимум, в точке В - нестрогий минимум). Точки максимума и минимума называются точками экстремума. Для того чтобы функция f (x) имела Экстремум в некоторой точке x0, необходимо, чтобы она была непрерывна в x0 и чтобы либо f`(x0) = 0 (точка А на рис. 1), либо f`(x0) не существовала (точка С на рис. 1). Если при этом в некоторой окрестности точки x0 производная f"(x) слева от x0 положительна, а справа отрицательна, то f (x) имеет в x0 максимум; если f"(x) слева от x0 отрицательна, а справа положительна, то - минимум (первое достаточное условие Экстремум). Если же f"(x) не меняет знака при переходе через точку x0, то функция f (x) не имеет Экстремум в точке x0 (точки D, Е и F на рис. 1). Если f (x) в точке x0 имеет п последовательных производных, причём f"(x0) = f``(x0) =...= f (n-1) (x0)=0, a f (n)(x0)¹0, то при п нечётном f (x) не имеет Экстремум в точке x0, а при п чётном имеет минимум, если f (n) (x0) > 0, и максимум, если f (n) (x0) < 0. Экстремум функции не следует смешивать с наибольшим и наименьшим значениями функции. Аналогично Экстремум функции одного переменного определяется Экстремум функции нескольких переменных. Необходимым условием Экстремум является в этом случае обращение в нуль или же несуществование частных производных первого порядка. Например, на рис. 2 частные производные равны нулю в точке М, на рис. 3 в точке М они не существуют. Если в некоторой окрестности точки М (х0, y0) существуют и непрерывны первые и вторые частные производные функции f (x, у) и в самой точке f"x = f"y = 0, D = f"" xx f"" уу > 0, то f (x, у) в точке М имеет Экстремум (максимум при f""xx < 0 и минимум при f""xx > 0); Экстремум в точке М не существует, если D < 0 (в этом случае М является т. н. седловиной, или точкой минимакса, см. рис. 4). Достаточные условия Экстремум функций многих переменных сводятся к положительной (или отрицательной) определённости квадратичной формы Sni, k=1 aikDxiDxk где aik - значение f""xixk в исследуемой точке.
48. Наибольшее и наименьшее значения функции.
Значение, принимаемое функцией в некоторой точке множества, на котором эта функция задана, называется наибольшим (наименьшим) на этом множестве, если ни в какой другой точке множества функция не имеет большего (меньшего) значения. Н. и н. з. ф. по сравнению с её значениями во всех достаточно близких точках называются экстремумами (соответственно максимумами и минимумами) функции. Н. и н. з. ф., заданной на отрезке, могут достигаться либо в точках, где производная равна нулю, либо в точках, где она не существует, либо на концах отрезка. Непрерывная функция, заданная на отрезке, обязательно достигает на нём наибольшего и наименьшего значений; если же непрерывную функцию рассматривать на интервале (т. е. отрезке с исключенными концами), то среди её значений на этом интервале может не оказаться наибольшего или наименьшего. Например, функция у = x, заданная на отрезке [0; 1], достигает наибольшего и наименьшего значений соответственно при x = 1 и x = 0 (т. е. на концах отрезка); если же рассматривать эту функцию на интервале (0; 1), то среди её значений на этом интервале нет ни наибольшего, ни наименьшего, так как для каждого x0 всегда найдётся точка этого интервала, лежащая правее (левее) x0, и такая, что значение функции в этой точке будет больше (соответственно меньше), чем в точке x0. Аналогичные утверждения справедливы для функций многих переменных.