
- •Основные сведения о матрицах. Операции над матрицами.
- •2.Определитель n-го порядка и их свойства.
- •Определители любого порядка. Свойства определителей.
- •6.Решение системы n линейных уравнений с n неизвестными методом обратных матриц.
- •7. Система m линейных уравнений с n неизвестными. Метод Гаусса.
- •9. Модель Леонтьева многоотраслевой экономики (балансовый анализ).
- •10. Расстояние между двумя точками. Деление отрезка в данном отношении. Площадь треугольника.
- •11. Линии первого порядка на плоскости.
- •12. Параллельность и перпендикулярность прямых.
- •13. Расстояние от точки до прямой.
- •14.Вектор. N-мерное векторное пространство. Линейные операции над векторами.
- •15. Линейная зависимость и независимость векторов. Базис. Разложение вектора по базису.
- •16. Предел функций в точке. Арифметические операций над пределами.
- •Первый замечательный предел
- •Второй замечательный предел
- •18. Бесконечно малые и бесконечно большие функций. Свойства.
- •Свойства бесконечно малых
- •19. Сравнение бесконечно малых.
- •22. Разрывы первого и второго рода.
- •23. Задача о производительности труда. Определение производной. Зависимость между непрерывностью и дифференцируемостью функции.
- •Понятие производной
- •24.Основные правила дифференцирования. Производные элементарных функций. Правила дифференцирования
- •25.Производные обратной и сложной функций.
- •26. Производные и дифференциалы высших порядков.
- •27.Понятие дифференциала функции. Применение дифференциала в приближенных вычислениях.
- •28.Основные теоремы дифференциального исчисления: Ферма, Ролля, Лагранжа.
- •29.Раскрытие неопределенностей.
- •30.Экстремумы функций. Необходимые и достаточные условие экстремума.
- •31.Наибольшее и наименьшее значение функций.
- •32.Выпуклость, вогнутость и точки перегиба кривой.
- •33.Асимптота графика функций. Общая схема исследования и построение графика функций.
- •34.Первообразная функций и неопределенный интеграл. Свойства неопределенного интеграла.
- •41.Дифференциальные уравнения с разделяющимися переменными.
- •42.Однородные линейные дифференциальные уравнения первого порядка.
- •43.Линейные дифференциальные уравнения первого порядка. Использование дифференциальных уравнении в экономике.
- •44. Определение функции двух переменных. Линии и поверхности уровня функции двух переменных.
- •45. Частные производные. Полное производное и полный дифференциал.
- •46. Производная по направлению. Градиент функции.
- •47. Экстремум функции многих переменных (необходимое и достаточное условия).
- •48. Наибольшее и наименьшее значения функции.
- •49. Метод Лагранжа.
- •50. Классическое и статистическое определение вероятности.
- •51. Элементы комбинаторики.
- •52. Теоремы сложения и умножения вероятностей.
- •53. Условная вероятность. Теорема сложения вероятностей для совместных событий.
- •54. Формула полной вероятности. Формула Бейеса.
- •55. Формула Бернулли. Формула Пуассона.
- •56. Понятие случайной величины. Закон распределения дискретных случайных величин.
- •57. Числовые характеристики дискретных случайных величин.
- •58. Биноминальный закон распределения.
- •59. Непрерывная случайная величина. Закон распределения вероятностей и основные числовые характеристики.
- •60. Функция плотности вероятностей.
- •61. Нормальное распределение.
- •62. Неравенство и теорема Чебышева. Закон больших чисел.
- •63. Задача математической статистики. Выборочный метод. Статистические оценки параметров распределения.
- •64. Несмещенные, эффективные и состоятельные оценки.
- •65. Интервальная оценка.
- •66. Корреляционный анализ. Линейная регрессия. Коэффициент корреляции.
24.Основные правила дифференцирования. Производные элементарных функций. Правила дифференцирования
Приведем основные правила для нахождения производной:
Производная постоянной равна нулю, то есть c' = 0.
Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, то есть
u(x) v(x))'
= u'(x)
v'(x).
v(x))'
= u'(x)
v'(x).
Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, то есть
(u(x)v(x))' = u'(x)v(x)+u(x)v'(x).
Следствие 1. Постоянный множитель можно выносить за знак производной:
(cu(x))' = cu'(x).
Производная частного двух дифференцируемых функций может быть найдена по формуле
(u(x)/v(x))' = (u'(x)v(x)-u(x)v'(x))/v2(x)
при условии, что v(x)≠ 0.
25.Производные обратной и сложной функций.
Пусть
![]() --
непрерывная функция, монотонная на
интервале
--
непрерывная функция, монотонная на
интервале
![]() .
Тогда, как мы доказали в гл. 3, функция
.
Тогда, как мы доказали в гл. 3, функция
![]() имеет
обратную функцию
имеет
обратную функцию
![]() ,
которая также является непрерывной и
монотонной функцией на интервале
,
которая также является непрерывной и
монотонной функцией на интервале
![]() ,
в который функция
,
в который функция
![]() переводит
интервал
.
Пусть
переводит
интервал
.
Пусть
![]() --
фиксированная точка и
--
фиксированная точка и
![]() --
точка, ей соответствующая. Тогда
--
точка, ей соответствующая. Тогда
![]() .
.
Теорема
4.5
Пусть
функция
имеет
в точке
![]() производную
производную
![]() .
Тогда обратная функция
.
Тогда обратная функция
![]() имеет
в соответствующей точке
имеет
в соответствующей точке
![]() производную
производную
![]() ,
которую можно отыскать по формуле
,
которую можно отыскать по формуле
|
(4.14) |
Доказательство.
Дадим аргументу
приращение
![]() ,
такое что
,
такое что
![]() ,
и рассмотрим соответствующее приращение
,
и рассмотрим соответствующее приращение
![]() ,
определяемое равенством
,
определяемое равенством
![]() .
Тогда, очевидно,
.
Тогда, очевидно,
![]() ;
при этом
;
при этом
![]() ,
а из монотонности функции
следует,
что
,
а из монотонности функции
следует,
что
![]() .
Поскольку как функция
,
так и функция
.
Поскольку как функция
,
так и функция
![]() непрерывны,
то условия
непрерывны,
то условия
![]() и
и
![]() эквивалентны.
Составим теперь разностное отношение
для функции
и
запишем для него очевидное равенство:
эквивалентны.
Составим теперь разностное отношение
для функции
и
запишем для него очевидное равенство:
![]() Теперь
перейдём в этом равенстве к пределу
при
и
учтём, что при этом
Теперь
перейдём в этом равенстве к пределу
при
и
учтём, что при этом
![]() тоже
стремится к 0:
тоже
стремится к 0:
![]() что
мы и хотели доказать.
Заметим, что, очевидно, из формулы (4.14)
следует, что
что
мы и хотели доказать.
Заметим, что, очевидно, из формулы (4.14)
следует, что
|
(4.15) |
если -- функция, обратная к .
Замечание
4.10
Нетрудно заметить из приведённого
доказательства, что если существует
производная
![]() ,
то разностное отношение
,
то разностное отношение
![]() стремится
к
стремится
к
![]() при
,
что соответствует вертикальной
касательной к графику
при
при
,
что соответствует вертикальной
касательной к графику
при
![]() (если
считать, что ось
(если
считать, что ось
![]() расположена
горизонтально, а ось
расположена
горизонтально, а ось
![]() --
вертикально).
--
вертикально).
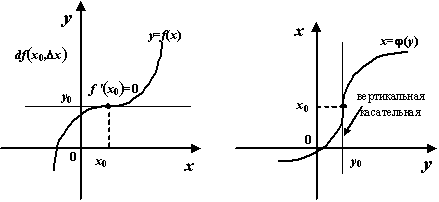
Рис.4.7.Графики функций и и касательные к ним при
Полученная
формула для производной обратной
функции имеет прозрачный геометрический
смысл. Заметим, что график как функции
,
так и обратной функции
изображается
на координатной плоскости
![]() одной
и той же линией, состоящей из точек
одной
и той же линией, состоящей из точек
![]() ,
где
или,
что то же самое,
.
Поэтому, если в точке
,
где
или,
что то же самое,
.
Поэтому, если в точке
![]() график
функции
имеет
касательную, образующую угол
график
функции
имеет
касательную, образующую угол
![]() с
осью
с
осью
![]() ,
то угол той же касательной с осью
будет,
очевидно, равен
,
то угол той же касательной с осью
будет,
очевидно, равен
![]() .
Тогда
.
Тогда
![]()
поскольку для обратной функции производная даёт тангенс угла наклона касательной по отношению к оси , на которой меняется аргумент функции .
Рис.4.8.Углы,
тангенсы которых равны
![]() и
,
дополняют друг друга до
и
,
дополняют друг друга до
![]()
Если u = f(x1,x2,x3….xn) , то в случае, когда x1,x2,x3….xn зависят только от одной переменной t, производная по t сложной функции(обыкновенная) вычисляется по формуле
![]() а
если f зависит от одной переменной х,
то формула принимает вид:
а
если f зависит от одной переменной х,
то формула принимает вид:
![]()
то есть совпадает с формулой для одномерного случая.
