Свойства бесконечно малых

• Сумма конечного числа бесконечно малых — бесконечно малая.

• Произведение бесконечно малых — бесконечно малая.

• Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.

• Если a_n — бесконечно малая последовательность, сохраняющая знак, то 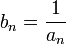— бесконечно большая последовательность.

19. Сравнение бесконечно малых.

 Пусть   и   — бесконечно малые при  . 1. Если  , то говорят, что   является бесконечно малой высшего порядка по сравнению с  . В этом случае пишут  . 2. Если  , где  —число, отличное от нуля, то говорят, что   и  — бесконечно малые одного и того же порядка. В частности, если  , то бесконечно малые   и   называются эквивалентными. Запись  ~  означает, что   и  —эквивалентные бесконечно малые. Если  , то это означает, что  . Таким образом,   является бесконечно малой высшего порядка по сравнению с  , т. е.  3. Если   и  —бесконечно малые одного и того же порядка, причем  , то говорят, что бесконечно малая   имеет порядок   по сравнению с  . Отметим некоторые свойства бесконечно малых величин: 1^o. Произведение двух бесконечно малых есть бесконечно малая высшего порядка по сравнению с сомножителями, т. е. если  , то   и  . 2^o. Бесконечно малые   и   эквивалентны тогда и только тогда, когда их разность  является бесконечно малой высшего порядка по сравнению с   и  , т. е. если  ,  . 3^o. Если отношение двух бесконечно малых имеет предел, то этот предел не изменится при замене каждой из бесконечно малых эквивалентной ей бесконечно малой, т.е. если  ,  ~ ,  ~ , то  .         Полезно иметь в виду эквивалентность следующих бесконечно малых величин:  если  , то

~           ~            ~           ~            ~             ~ 

20. Непрерывность функций в точке. Точки разрыва. Представление о  непрерывности   функции  интуитивно связано у нас с тем, что её графиком является плавная, нигде не прерывающаяся линия. При рассмотрении графика такой  функции  y = f(x) мы видим, что близким значениям аргумента соответствуют близкие значения  функции : если независимая переменная  приближается к  точке  x₀, то значение  функции  y = f(x) неограниченно приближается к значению  функции  в точкеx₀, т.е. к f(x₀).

Дадим строгое определение  непрерывности   функции . Итак, пусть имеем функцию y = f(x).

Функция y = f(x) называется непрерывной  в   точке  x₀, если она определена в этой точке и в некоторой окрестности содержащей x₀ и Таким образом, можно сказать, что функция непрерывна в точкеx₀, если выполнены 3 условия:

1. она определена в точке x₀ и в некоторой её окрестности;

2. имеет предел при x → x₀;

3. этот предел равен значению функции в точке x₀.

Формулу (1) можно записать в виде  , т.к.  . Это означает, что для того, чтобы найти предел непрерывной функции при x → x₀, достаточно в выражение функции подставить вместо аргументах его значение x₀.

Непрерывные функции обладают следующими свойствами.

Теорема 1. Если функции f(x) и g(x) непрерывны в точке x₀, то их сумма φ(x) = f(x) + g(x) также есть непрерывная функция в точке x₀.

Доказательство. Так как функции f(x) и g(x) непрерывны в точке x₀, то исходя из определения можно написать  . Тогда на основании свойств пределов будем иметь

.Эта теорема справедлива для любого конечного числа слагаемых.

Следующие две теоремы докажите самостоятельно аналогично теореме 1.

Теорема 2. Произведение двух непрерывных функций есть функция непрерывная.

Теорема 3. Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль.

Если функцию можно представить в виде y = f(u), где u =φ(x), т.е. если функция зависит от переменной через промежуточный аргумент u, то называется сложной функцией переменной x.

Справедлива следующая теорема.

Теорема 4. Если функция u = φ(x) непрерывна в точкеx₀ и принимает в этой  точке  значение u₀ = φ(x₀), а функция f(u) непрерывна в  точке  u₀, то сложная функция y = f(φ(x)) непрерывна в  точке  x₀.

Используя эти теоремы можно доказать следующий результат.

Теорема 5. Всякая элементарная функция непрерывна в каждой  точке , в которой она определена.

Заметим, что если функция y = f(x) непрерывна  в   точке  x₀ и её значение в этой  точке  отлично от 0, f(x₀) ≠ 0, то значения функции f(x) в некоторой окрестности  точки x₀ имеют тот же знак, что и f(x₀), т.е. если f(x₀) > 0, то найдётся такое δ > 0, что на интервале(x₀– δ;x₀+ δ) f(x) > 0 (в этой окрестности значения функции f(x) очень мало отличаются от своего предела).Определение. Функция   имеет точку разрыва при   , если она определена слева и справа от точки   , но в точке   не выполняется хотя бы одно из условий непрерывности.

Точки разрыва функции   :

1. Точка устранимого разрыва;

2. Точка разрыва первого рода;

3. Точка разрыва второго рода.

Точка   является точкой устранимого разрыва, если функция в точке   не определена и существуют равные конечные пределы   и   , т.е.  .

21.Свойства функций непрерывных в точке и на отрезке.

Теорема 9 (локальные  свойства   непрерывных   функций ).

Пусть  функция  f:E R  непрерывна   в   точке  a. Тогда f(x) ограничена в некоторой окрестности  точки  a.

Пусть  функция  f(x)  непрерывна   в   точке  a  и  f(a) 0, то в некоторой окрестности  точки  a все значения  функции положительны или отрицательны вместе с f(a).

Если f(x), g(x) -  непрерывны   в   точке  a, то  функции : f(x)+g(x), f(x)g(x), f(x)/g(x) (при g(a) 0 )  непрерывны   в   точке  a.

Если  функция  g(x):Y R  непрерывна   в   точке  b Y, а  функция f:E Y  непрерывна   в   точке  a, f(a) = b, тогда композиция g_° f также непрерывна   в   точке  a.

Данная теорема следует из определения непрерывности  функции   и соответствующих  свойств  предела  функции .

 Свойства   функций ,  непрерывных   на   отрезке .

              Свойство  1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897)- немецкий математик)).  Функция ,  непрерывная   на   отрезке , ограничена на этом  отрезке , т.е.  на   отрезке  [a, b] выполняется условие –M  f(x)  M.

Доказательство этого  свойства  основано на том, что  функция ,  непрерывная   в   точке  х₀, ограничена в некоторой ее окрестности, а если разбивать  отрезок  [a, b] на бесконечное количество  отрезков , которые “стягиваются” к  точке  х₀, то образуется некоторая окрестность  точки  х₀.

 Свойство  2:  Функция ,  непрерывная   на   отрезке  [a, b], принимает на нем наибольшее  и  наименьшее значения.

Т.е. существуют такие значения х₁ и х₂, что f(x₁) = m,  f(x₂) = M, причем

m  f(x)  M

 Отметим эти наибольшие  и  наименьшие значения  функция  может принимать  на   отрезке   и  несколько раз (например – f(x) = sinx).

Разность между наибольшим  и  наименьшим значением  функции   на   отрезке  называется колебанием  функции   на   отрезке .

 Свойство  3: (Вторая теорема Больцано – Коши).  Функция ,  непрерывная   на   отрезке  [a, b], принимает на этом  отрезке  все значения между двумя произвольными величинами.

 Свойство  4: Если  функция  f(x)  непрерывна   в   точке  х = х₀, то существует некоторая окрестность  точки  х₀, в которой  функция  сохраняет знак.

 Свойство  5: (Первая теорема Больцано (1781-1848) – Коши). Если  функция  f(x) непрерывная   на   отрезке  [a, b]  и  имеет на концах  отрезка  значения противоположных знаков, то существует такая  точка  внутри этого  отрезка , где f(x) = 0.

 Т.е. если sign(f(a))  sign(f(b)), то  х₀: f(x₀) = 0.

 Определение.  Функция  f(x) называется равномерно  непрерывной   на   отрезке  [a, b], если для любого >0 существует >0 такое, что для любых  точек  х₁[a,b]  и  x₂[a,b] таких, что

х₂ – х₁<  верно неравенство     f(x₂) – f(x₁) < 

  Отличие равномерной непрерывности от “обычной” в том, что для любого  существует свое , не зависящее от х, а при “обычной” непрерывности  зависит от   и  х.

 Свойство  6: Теорема Кантора (Кантор Георг (1845-1918)- немецкий математик).  Функция ,  непрерывная   на   отрезке , равномерно  непрерывна  на нем.

(Это  свойство  справедливо только для  отрезков , а не для интервалов  и  полуинтервалов.)

Свойство  7: Если  функция  f(x) определена, монотонна  и   непрерывна  на некотором промежутке, то  и  обратная ей  функция  х = g(y) тоже однозначна, монотонна  и  непрерывна .