
- •1.Числовой ряд. Сходимость ряда. Необходимый признак сходимости ряда. Примеры.
- •2. Признаки сравнения для рядов с положительными членами.
- •3,4. Признаки Даламбера и Коши.
- •6.Знакочередующийся ряд. Теорема Лейбница. Оценка остатка ряда.
- •7. Знакопеременные ряды. Абсолютная сходимость. Условная сходимость. Примеры. Действия с абсолютно сходящимися рядами.
- •8. Функциональный ряд. Область сходимости. Равномерная, поточечная сходимость.
- •10,11.Непрерывность суммы степенного ряда. Интегрирование и дифференцирование степенного ряда.
- •12,13. Степенной ряд. Теорема Абеля. Область сходимости. Равномерная сходимость.
- •14. Ряд Тейлора. Разложение функции в ряд Тейлора. Необходимое и достаточное условие разложения в ряд Тейлора. Примеры разложения основных функций в ряд Тейлора.
- •17. Ряд Фурье для функций с периодом 2l.
- •19. Разложение в ряд Фурье непериодических функций.
- •20. Комплексная форма тригонометрического ряда Фурье.
- •22. Синус и косинус преобразований Фурье.
- •23. Определение функции комплексного переменного и её геометрический смысл.
- •29. Аналитические, гармонические функции.
- •30. Геометрический смысл модуля и аргумента производной.
- •31. Интеграл от фкп.
- •32. Классификация изолированных особых точек.
- •33. Нули аналитической функции и их связь с полюсом.
- •34. Неравенство Коши, теорема Лиувилля, основная теорема алгебры.
- •35. Интегральная теорема Коши
33. Нули аналитической функции и их связь с полюсом.


34. Неравенство Коши, теорема Лиувилля, основная теорема алгебры.


35. Интегральная теорема Коши
Теорема Коши
Рассм. инт-лы от одноз-ных аналит. ф-ций. Т1. (Коши для односвязн. обл.) Пусть ф-ция f(z) аналит. в односвязн. обл. Д, тогда для люб. замкн. контура ГД, инт. .
док-во.
Проведем док-во при дополн. предполож-ии,
что производная f.`(z)
непрер. в Д. В силу р-ва
для
вып-ия условия, что
=0
необход. и дост., чтобы инт.
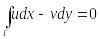 и
и
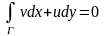 (1)
.
Если P(x,y)
и Q(x,y)
непр. действит. ф-ции в 1-связной обл. Д,
имеющ. в Д непрер. частные произв-ные 1
порядка, то
(1)
.
Если P(x,y)
и Q(x,y)
непр. действит. ф-ции в 1-связной обл. Д,
имеющ. в Д непрер. частные произв-ные 1
порядка, то
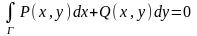 .
Равносильны след. условию: ∂P/∂y-∂Q/∂x=0
(2).
Применительно к инт. из (1)усл. (2) имеет
вид ∂u/∂y=-∂v/∂x,
∂u/∂x=∂v/∂y
(3)
. Непрер-ность частных произв-ых ф-ций
u
и v
вытекает из непрер. f
`(z),
но усл. (3) совпадает с усл. Коши-Римана,
кот. вып. в силу предполож. о том, что
ф-ция f(z)
явл. аналит. в Д. Т.О. справедливы ра-ва
(1), а значит и р-во
.
□
.
Равносильны след. условию: ∂P/∂y-∂Q/∂x=0
(2).
Применительно к инт. из (1)усл. (2) имеет
вид ∂u/∂y=-∂v/∂x,
∂u/∂x=∂v/∂y
(3)
. Непрер-ность частных произв-ых ф-ций
u
и v
вытекает из непрер. f
`(z),
но усл. (3) совпадает с усл. Коши-Римана,
кот. вып. в силу предполож. о том, что
ф-ция f(z)
явл. аналит. в Д. Т.О. справедливы ра-ва
(1), а значит и р-во
.
□
Если f(z) явл. аналит. в замкнут. односвяз. обл. Д~, то в качестве Г можно взять границу этой обл. Пусть Д n-связная обл., граница кот. сост. из внеш. контура Г, и внутрен. конт. Г2,…,Гn.
Т2.(Коши для n-связн. обл.) Пусть f(z) аналит. в n-связн. обл. Д~,тогда инт. от ф-ци f по границе Д~ =0, при этом предполож., что обход граничных кривых проводитя в таком направл., чтобы Д оставалась слева.
Т2*.
Если ф-ция f(z)
аналит. в n-связн.
обл. Д и все граничные контуры Г1 и Г2,…,Гn
обход. в одном и том же направл., то
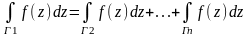 (5),
где Г1-внеш. контур, охват. остальные.
(5),
где Г1-внеш. контур, охват. остальные.
док-во. следут из ф-лы (4), если у контуров Г2,…,Гn или у контура Г1 изменить направл. обхода на против-ый и перенести в др.часть р-ва(4)соотв. инт.
След-e 1. Пусть f(z) аналит. в 1-связ. обл. Д и пусть a,b Д, тогда инт. по всем кривым идущим из a в b, лежащ. внутри Д, равны м\д собой.Т.е. инт. зависит не от пути, а лишь от его нач. и конечной точки.
Т-ки. z, в кот. 1-значн. f(z) явл. аналит., наз.регулярными или правильными т. ф-ции f(z). Т., в кот. f(z) не явл. аналит., в том числе точки, в кот. f(z) не опред. наз. особыми. Особая точка z0, в кот. найдется такая окрестность с центром в т. z0, в каждой точке кот. за исключением точки z0 ф-ция f(z) явл. аналит. наз. изолированной.
След-e2. (неизмен-ость инт. при деформации пути инт.) Инт. от аналит. ф-ции f(z) по кривой Г(замкн. или незамкн.) не изменят своей величины при любой непрер. деформации кривой Г, если только при этой деформации Г не пересечет особых точек ф-ции f(z). В случае незамкнутой кривой Г подразумевается, что при деформации начало и конец Г остается неподвижным.
36. Интегральная формула Коши


37. вычисление вычетов в простых полюсах
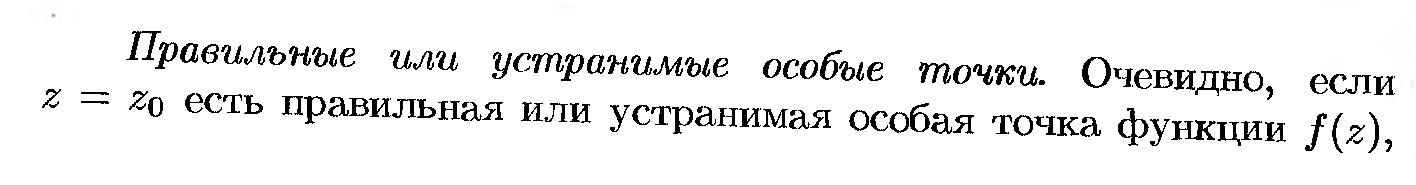

38. вычисление вычетов к-го порядка

39. Ряды Лорана


40. Основная теорема о вычетах.
Пусть Г – замкнутый контур, лежащий в области аналитичности функции f(z), и пусть f(z) аналитична во всех точках внутри Г за исключением n изолированных особых точек z1,z2,…,zn. Тогда интеграл от f(z) по Г равен сумме вычетов в этой особой точке, умноженной на 2i:
 (1)
(1)
Доказательство: Пусть внутри Г расположены изолированные особые точки z1,z2,…,zn (рис. 1)
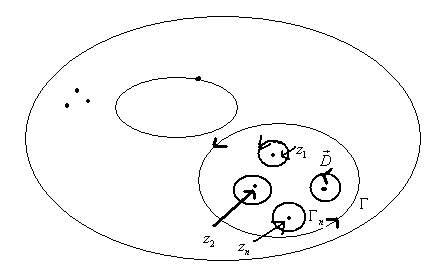 Рис.
1
Рис.
1
Окружим
любую из этих точек zk
достаточно малыми окружностями
![]() так, чтобы любая окружность k
заключала внутри себя только одну особую
точку zk,
целиком лежащую внутри Г
и не пересекающуюся с другими окружностями.
так, чтобы любая окружность k
заключала внутри себя только одну особую
точку zk,
целиком лежащую внутри Г
и не пересекающуюся с другими окружностями.
Функция
f(z)
аналитична в замкнутой (n+1)–связной
области
![]() ,
ограниченной внешним контуром Г
и внутренними контурами 1,
2,
…, n.
По теореме Коши для многосвязной области
,
ограниченной внешним контуром Г
и внутренними контурами 1,
2,
…, n.
По теореме Коши для многосвязной области
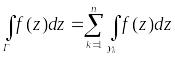 (2)
(2)
Т.к.
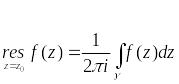 (3),
то для любого интеграла в правой части
(2) справедливо равенство
(3),
то для любого интеграла в правой части
(2) справедливо равенство
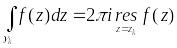 .
Подставляя эти равенства в (2), приходим
к (1).
.
Подставляя эти равенства в (2), приходим
к (1).
41. Оригинал и изображение



42. Свойства преобразований Лапласа. Линейность, теорема подобия.



43. Теорема запаздывания.
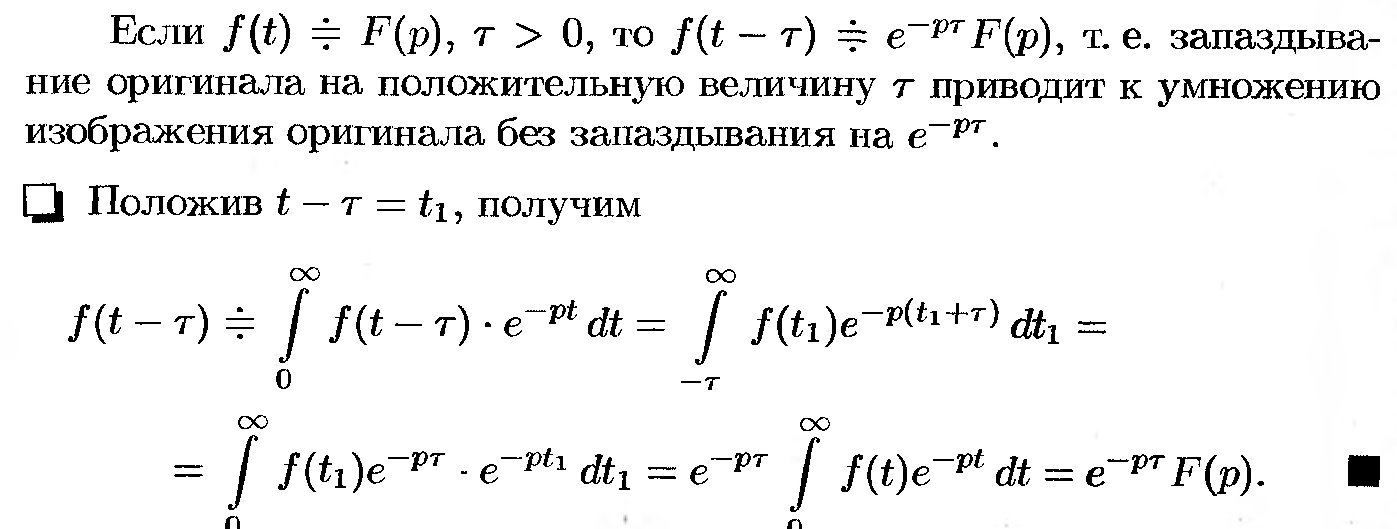
44. Теорема затухания.
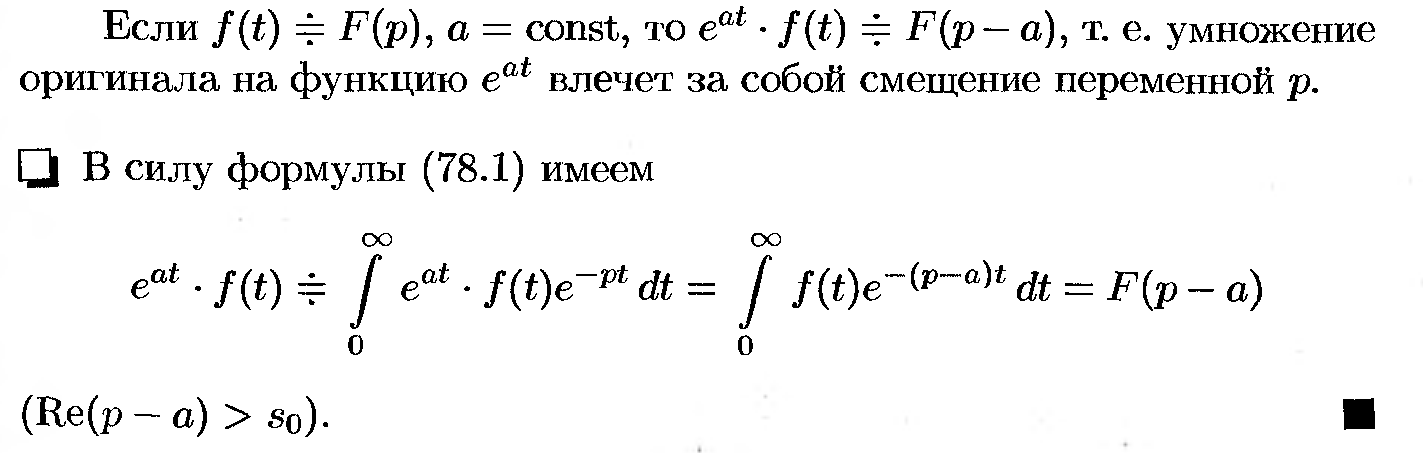
45. Дифференцирование оригинала.
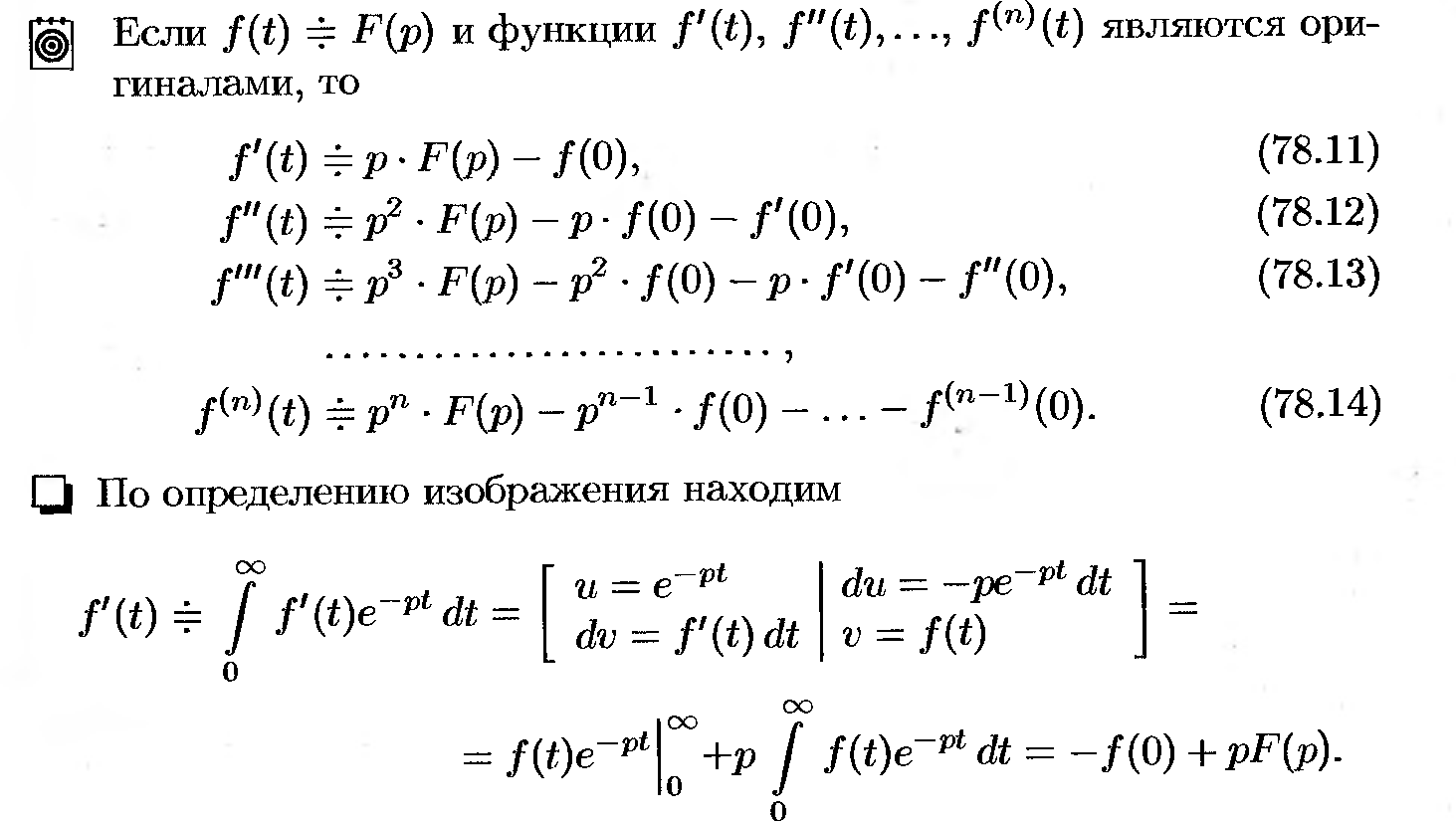
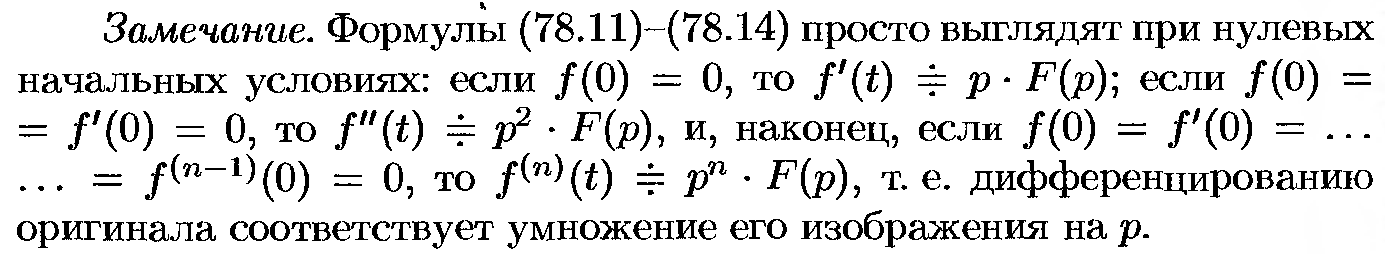
46. Дифференцирование изображений
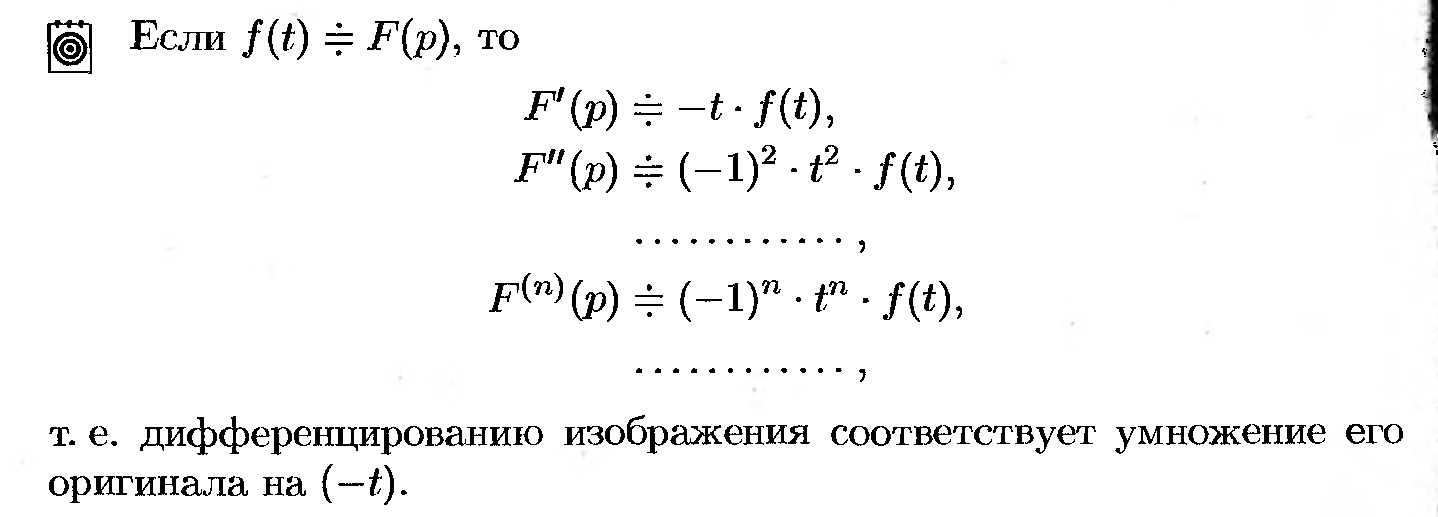
47. Интегрирование оригинала.
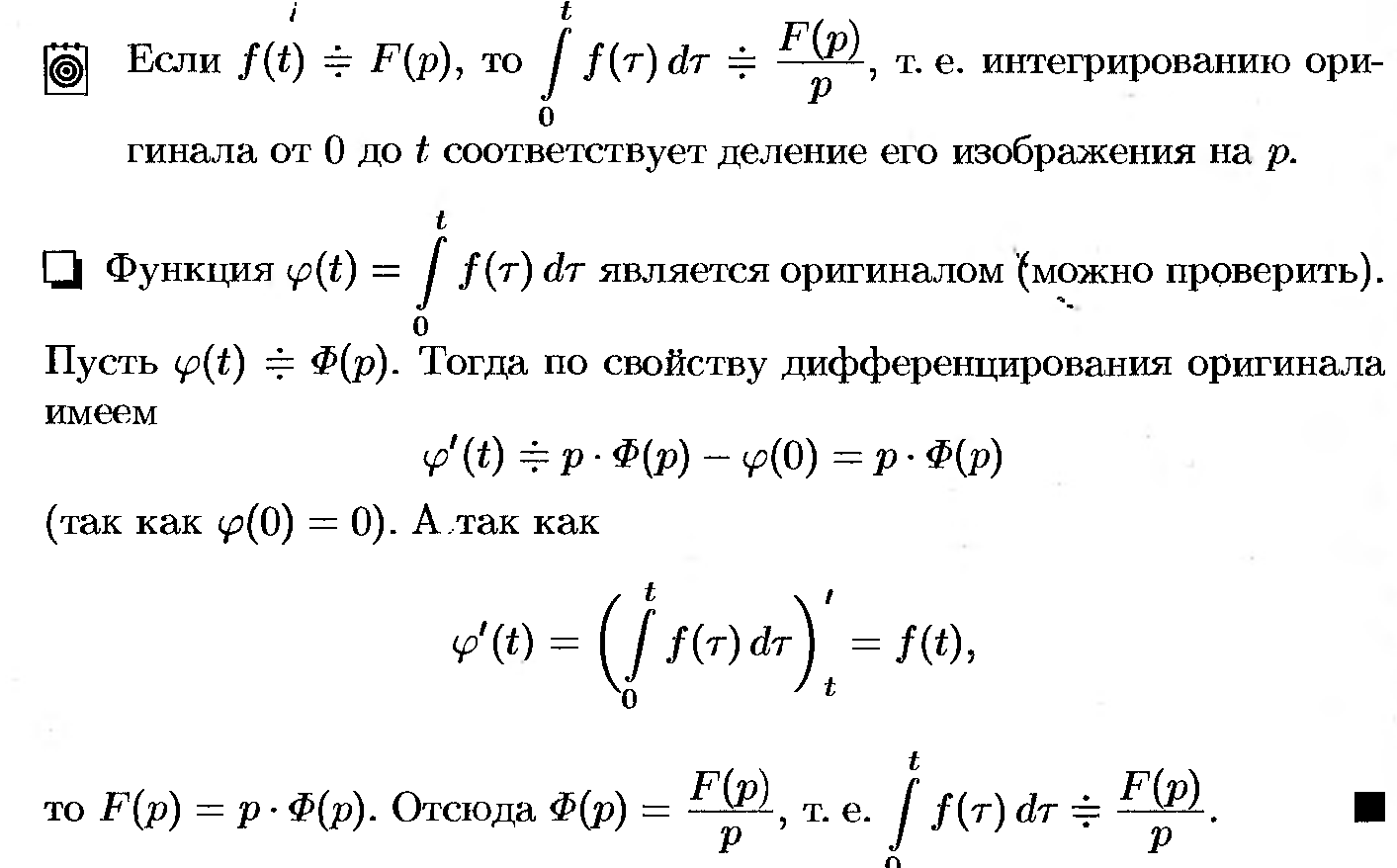
48. Интегрирование изображения.

49. Свертка оригиналов.
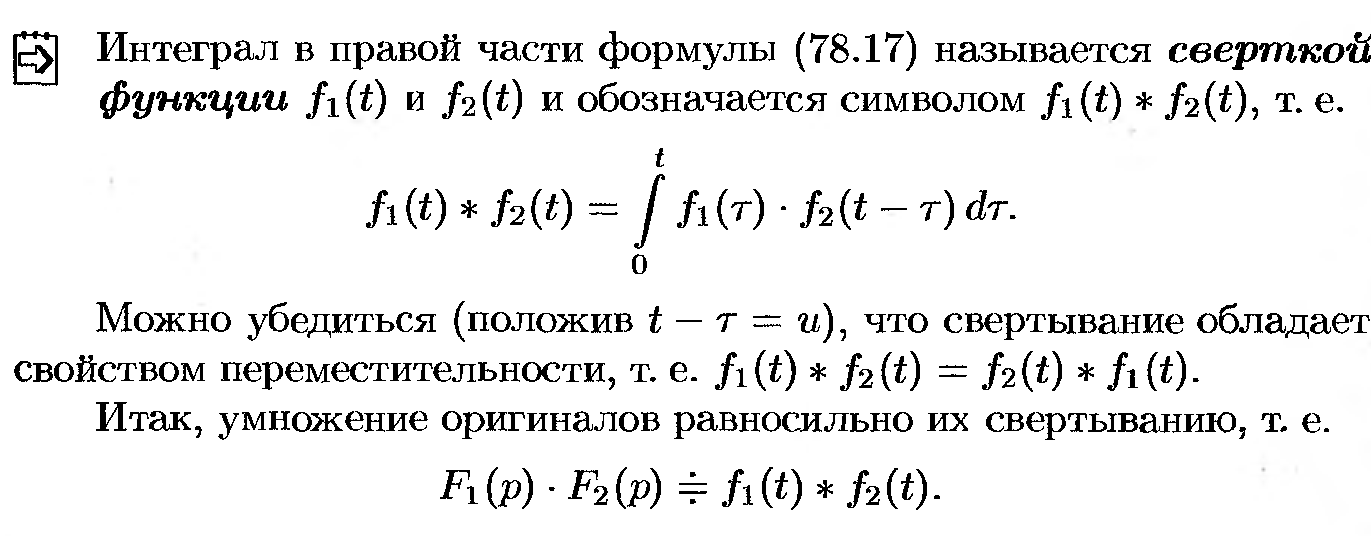
50. Теорема Бореля.
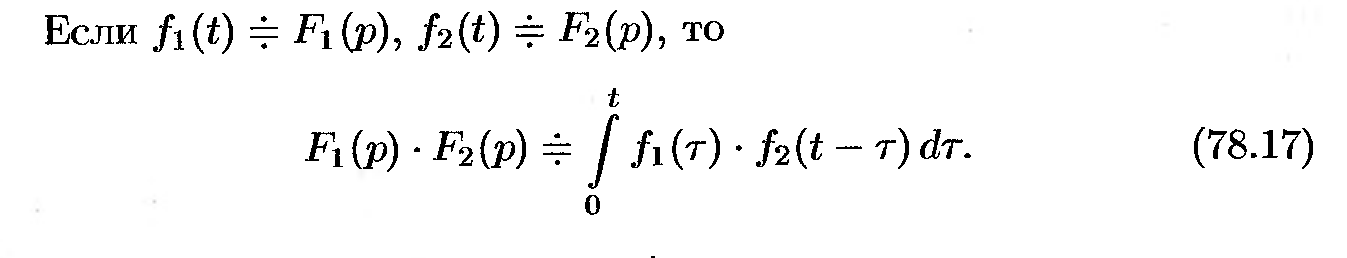
Изображение свёртки двух оригиналов равно произведению изображений свёртываемых оригиналов.
51. Интеграл и формула Дюамеля.

52. Формула обращения Меллина, теоремы разложения.



