29. Аналитические, гармонические функции.

Функция w=f(z) дифференцируемая не только в самой точке z₀, но и в некоторой окрестности этой точки называется аналитической в точке z₀. Если f(z) является аналитической в каждой точке области Д, то она называется аналитической (регулярной) в области Д.

Из свойств производных сразу следует , что если f(z) и g(z) аналитические функции в области Д, То функции f(z)+g(z), f(z)-g(z), f(z)_*g(z) и f(z)/g(z) (g(z)≠0) являются аналитическими в Д. Из теоремы о производной сложной функции вытекает следующее утверждение: если функция u=u(z) аналитична в области Д и отображает Д в область Д' переменного u , а функция w=f(u) аналитична в области Д', то сложная функция w=f[u(z)] аналитична в Д.

Введем понятие функции, анатичн. в замкнутой области Д^-. Отличие от открытой области в том, что добавляются точки границы, имеющие окрестности принадлежащие Д^-. Поэтому производная в этих точках не определена. Функция f(z) называется аналитической в замкнутой области Д^- , если ее можно продолжить в некоторою более широкую область Д, содержащую Д^-, до аналитической в Д функции.

30. Геометрический смысл модуля и аргумента производной.

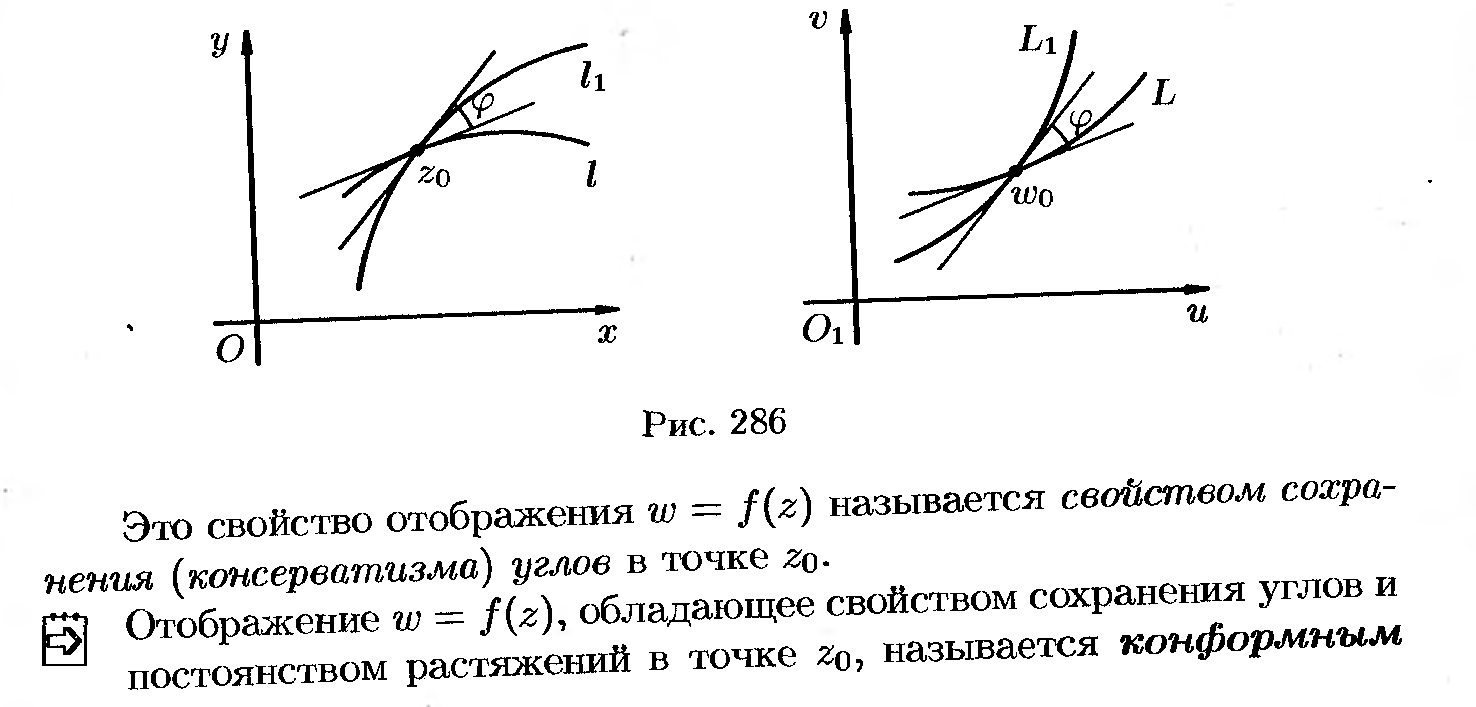
31. Интеграл от фкп.

Рассм. гладкую кривую Г на компл. пл-сти, заданную параметр. ур-ниями: x=x(t), y=y(t), α<=t<=β (1). Эти ур-ния запишем в компл. виде z(t)=x(t)+i y(t), α<=t<=β (2).

При изменении параметра t (α<=t<=β), соотв. точка будет двигаться по кривой Г. Поэтому у-ния (1) и (2) не только опред. точку кривой Г, но и задают направление обхода этой кривой. Кривая Г с заданным направл. обхода наз. ориентированной кривой.

Пусть в обл. Д из С задана непрерывная ф-ция f(z)=u(x,y)+i v(x,y), и пусть Г лежит в Д. Чтобы ввести понятие 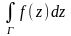от ф-ции f(z) по кривой Г, определим диффф-ал dz равенством dz=dx+id y. Подынт-ое выражение преобразуем к виду: f(z)dz=(u+iv)(dx+idy)=udx-vdy+i(vdx+udy). Т.О. 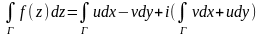(3).

В правую часть ра-ва (3) входят 2 действит-ых кри-2 от действит. ф-ций u и v. В силу параметр-ского задания кривой (2), инт. в правой части в (3) сведутся к двум инт. от ф-ций действит. переменной t по отр. [α;β] 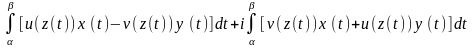(4).

Это выраж. преобраз. к виду: .

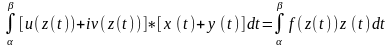Инт-ом вдоль Г от ф-ции компл. переменного, наз. число, обознач. и вычисляемое по формуле 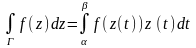(5), где z(t)=x(t)+i y(t), α<=t<=β – ур-ние кривой Г, а z`(t)=x`(t)+i y`(t). Установим осн. св-ва инт. :

1. линейность: для люб. компл. постоянного a и b - 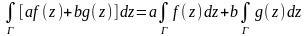. Это рав-во следует из р-ва (5) и св-ва инт. по отрезку.

2. адитивность: если Г разбита участками Г1 и Г2, то 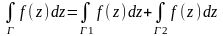. Док-во. Пусть Г с концами a и b разбита т. с на две части. Кривую Г1 с концами a,c и Г2 с концами c,b. Пусть Г задается у-ниями z=z(t), α<=t<=β. Причем a=z(α), b=z(β), c=z(γ). Тогда у-ния Г1 и Г2 будут z=z(t),где α<=t<= γ и γ<=t<=β соотв. Применяя фор-лу (5) и соотв. св-во инт. по отрезку получим:

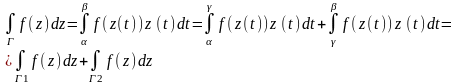
3. При изменении направл. обхода кривой инт. меняте знак.

│ │ не превосходит знач. криволин. инт. от модуля ф-ции по длине кривой (кри-1: │ │):│ │≤ =

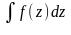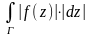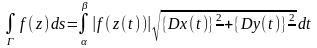
Теорема Коши

Рассм. инт-лы от одноз-ных аналит. ф-ций. Т1. (Коши для односвязн. обл.) Пусть ф-ция f(z) аналит. в односвязн. обл. Д, тогда для люб. замкн. контура ГД, инт. .
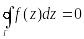