17. Ряд Фурье для функций с периодом 2l.

18.Разложение четных функций в тригонометрический ряд.

f(x)=f(-x) , xR¹

a_n=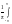 f(x)cosnxdx= 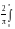f(x)cosnxdx

b_n=0

f(x)= 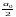+ 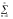a_ncosnx - разложение по косинусам.

Разложение нечетных функций в тригонометрический ряд.

f(x)= - f(-x); a₀=0, a_n=0

f(x)= 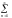b_nsinnx

b_n= f(x)sinnxdx

- разложение по синусам.

Примеры: 1) f(x)=x

a₀=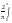 1dx=2; a_n=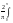 1cosnxdx=0

f(x)= 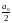=1

2) Функция

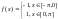
b_n=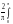 1sinnxdx=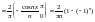

19. Разложение в ряд Фурье непериодических функций.

20. Комплексная форма тригонометрического ряда Фурье.

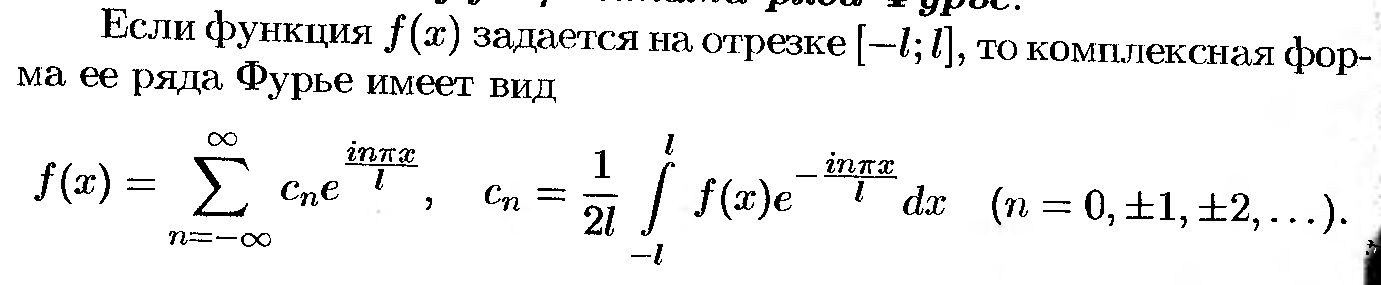
21. Интеграл Фурье.

Пусть ф-ция f(x) представлена на отрезке (-l;l)

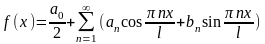, где

; ;

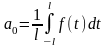
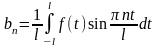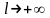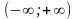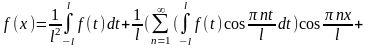
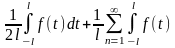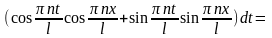
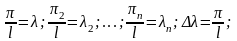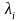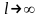
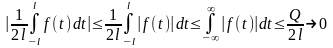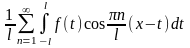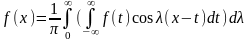f(x) абсолютно интегрируема на , тогда * Ф-ция , стоящая в правой части явл. Ф-цией от переменных . Устремим . Можно показать что если ф-ция f(x) кусочно-монотонная и ограничена, то тогда превращается в следующее (при ) -интеграл Фурье.

22. Синус и косинус преобразований Фурье.

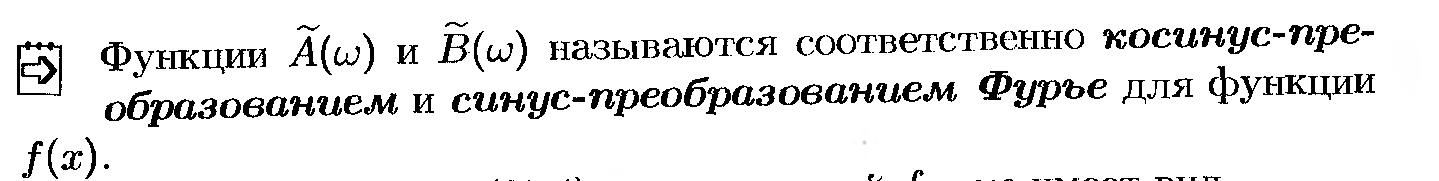
23. Определение функции комплексного переменного и её геометрический смысл.

Пусть Д некоторое мн-во компл. чисел. Однозначной функцией компл. переменного наз-ся правило по которому компл. числу z соответствует единственное компл. число w. Такое соответствие обознач. w=f(z) или f :w - >z. Мн-во Д наз-ся мн-вом определения функции f. Если обозначить z=x+iy, w=u+iv, то задание функции w=f(z) компл. переменного равносильно заданию на том же мн-ве 2-х функций действ. переменных х и у, принимающих действ. значения u=u(x,y) и v=v(x,y). Наряду с плоскостью z=x+iy рассмотрим также плоскость компл. переменного w=u+iv с координатами (u,v). Когда т. z пробегает мн-во Д на плоскости переменного z соответственно т. w пробегает другое

мн-во Е. Т.о. однозначная ф-ция w=f(z) отображает мн-во Д на мн-во Е, т.е. каждой т. z из Д ставим в соответствие точку w из Е. Точка w наз-ся образом точки z, а т. z прообразом т. w при отображении w=f(z). Точка w может иметь несколько прообразов.

Предел функции комплексного переменного

Введем понятие предела функции w=f(z) в точке. Пусть задана т. z₀ из С и δ>0. Проколотой δ- окрестностью

т. z₀=0 наз-ся δ-окрестность этой точки за исключением самой т. z₀ , т.е. внутренность круга радиуса δ с центром z₀ из которого удален центр z₀. Это мн-во можно записать в виде 0<| z-z₀ |<δ. Пусть функция w=f(z) определена в некоторой проколотой окрестности т z₀. Число А наз-ся пределом функции w=f(z) в т. z₀ , если для любого ε>0 найдется такое δ>0, δ=δ(ε), что для всех точек проколотой окрестности т. z₀ выполняется неравенство |f(z)-A|<ε. Наличие у функции f(z) предела в точке А записывается в виде

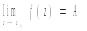
и означает следующее: для любой окрестности U_A т. А найдется такая проколотая окрестность т. z₀ , что для всех точек z проколотой окрестности соответствующее значение f(z) лежит в U_A . В такой форме определение предела охватывает и случай z=∞ и А=∞. Под проколотой окрестностью т. z=∞ понимается мн-во |z|>R. Данное определение предела для функции аналогично опред-нию предела для функции действ. переменных. Поэтому важные теоремы сохраняют силу и для фуции компл. переменного. Если функция f(z) определена лишь в области Д , то для граничной точки z₁ не существует проколотой окрестности, в которой задано значение f(z) . Число А наз-ся пределом функции w=f(z) в граничной точке z₁, если для любого ε>0 найдется такое δ>0, что для всех точек проколотой δ-окрестности точки z₁ принадлежащей области Д выполняется неравенство

|f(z)-A|<ε.

Непрерывность функций комплексного переменного.

Наличие у функции f(z) предела в точке А записывается в виде

и означает следующее: для любой окрестности U_A т. А найдется такая проколотая окрестность т. z₀ , что для всех точек z проколотой окрестности соответствующее значение f(z) лежит в U_A . В такой форме определение предела охватывает и случай z=∞ и А=∞. Под проколотой окрестностью т. z=∞ понимается мн-во |z|>R. Данное определение предела для функции аналогично опред-нию предела для функции действ. переменных. Поэтому важные теоремы сохраняют силу и для фуции компл. переменного. Если функция f(z) определена лишь в области Д , то для граничной точки z₁ не существует проколотой окрестности, в которой задано значение f(z) . Число А наз-ся пределом функции w=f(z) в граничной точке z₁, если для любого ε>0 найдется такое δ>0, что для всех точек проколотой δ-окрестности точки z₁ принадлежащей области Д выполняется неравенство |f(z)-A|<ε. Функция w=f(z), определенная в окрестности (не проколотой!) точки z₀ наз-ся непрерывной в т. z₀, если

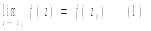
Непрерывность функции w=f(z)=u(x,y)+iv(x,y) в т. z₀=x₀+iy₀ эквивалентна непрерывности двух действ-ных функций u(x,y) и v(x,y) двух действ. переменных х и у в т. (x₀,y₀). Функция w=f(z) , определенная в области Д наз-ся непр-ной в этой области, если f(z) непрерывна в каждой точке области Д. Функция w=f(z) наз-ся непр-ой в замкнутой области Д', если она определена в Д' и для каждой т. z₀ из Д выполнено равенство (1). Зафиксируем т. z₀ и возьмем другую т. z из Д. Тем самым аргумент изменяется на величину ∆z=z-z₀=∆x+i∆y, наз-ся приращением аргумента. Соотв-щее изменение функции ∆w=f(x)-f(z₀)=∆u+i∆v наз-ся приращением

24.

25. Показательная функция

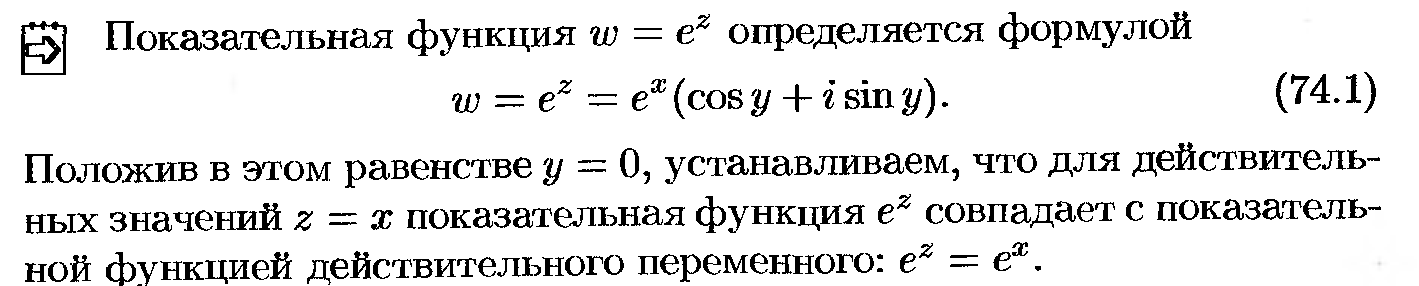
26. Логарифмическая функция

27. Обратная тригонометрическая ФКП.

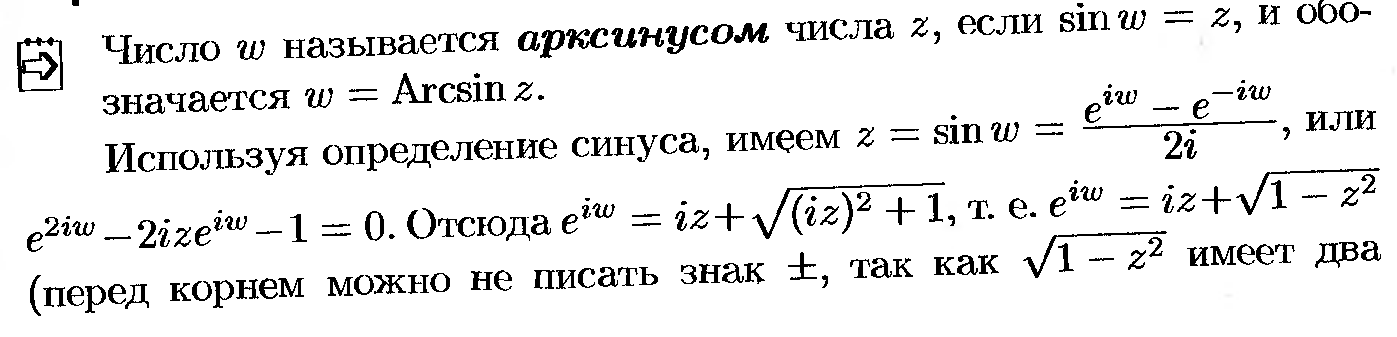
28. Производная и дифференциал.

Определения производной и дифференциала функции комплексного переменного дословно совпадают с соответствующими определениями для функции одного действительного переменного. Пусть w=f(z)=u+iv определена в некоторой окрестности U точки z₀. Дадим независимой переменной z=x+iv приращение ∆z=∆x+i∆y , не выходящее за пределы окрестности U. Тогда соответствующая функция w=f(z). получит соответствующее приращение ∆w=f(z₀+∆z)-f(z₀). Производной функции w=f(z) в точке z₀ называется предел отношения приращения функции ∆w к приращению аргумента ∆z при ∆z->0. Производная обозначается f'(z), w', dw/dz и т.д. Определение производной можно записать в виде

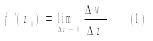
Предел (1) может и не существовать тогда говорят , что функция w=f(z) не имеет в точке z₀ производной. Функция w=f(z) называется дифференцируемой в точке z₀ если она определена в некоторой окрестности U точки z₀ и ее приращение ∆w можно представить в виде:

∆w=A∆z+α(∆z)_*∆z (2)

где число А не зависит от ∆z, а α(∆z)-бесконечно малая функция ∆z->0. Выражение f'(z)∆z называется дифференциалом переменного z и обозначается dz . Т.о образом dw=df(z₀)=f'(z₀)dz. Дифференциал есть главная линейная часть приращения функции.

Функция u=u(x,y) действительных переменных х и у называется дифференциалом в точке Р₀(х₀,у₀), если она определена в некоторой окрестности т. Р₀ и ее полное приращение ∆u=u(x₀+∆x,y₀+∆y)-u(x₀,y₀) представлено в виде

∆u=B∆x+C∆y+β(∆x,∆y)∆x+γ(∆x,∆y)∆y (3)

где В и С -действительные числа , независящие от ∆x и ∆y, а β и γ- действительные функции переменных ∆x и ∆y стремящиеся к 0 при ∆x->0 и ∆y->0. Если функция u дифференцируема в точке Р₀ то она имеет частные производные в Р₀, причем

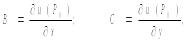
но, в отличие от функции одного переменного из существования частных производных функции u(x,y) еще не следует ее дифференцруемость.

Условия Коши-Римана.

Теорема1:Пусть функция комплексно переменного w=f(z)=u(x,y)+iv(x,y) определена в окрестности т. z₀=x₀+iy₀. Для того чтобы f(z) была диффер-мой в т. z₀ необходимо и достаточно, чтобы функции u(x,y) и v(x,y) были дифф-мы в т. (x₀+y₀) и чтобы в этой точке выполнялись условия :

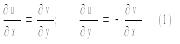
Равенства (1) называются условиями Коши-Римана.

Док-во: Необход.. Пусть функция w=f(z) диффер-ма в точке z₀ т.е. ∆w=∆u+i∆v=f'(z₀)∆z+α(∆z)∆z (2).

Обозначим f'(z₀)=a+ib ; α(∆z)=β(∆x,∆y)+iγ(∆x,∆y), ∆z=∆x+i∆y, где β и γ-действ-ые функции переменных х и у , стремятся к 0 при ∆x-> u ∆y->0. Подставляя эти равенства в (5) и выделяя действительные и мнимые части , получим: ∆u+i∆v=(a+ib)(∆x+i∆y)+(β(∆x,∆y)+iγ(∆x,∆y))(∆x+i∆y)=

=(a∆x-b∆y+β(∆x,∆y)∆x-γ(∆x,∆y)∆y)+

+i(b∆x+a∆y+β(∆x,∆y)∆y+γ(∆x,∆y)∆x) (3)

Поскольку равенство компл. чисел равносильно равенству их действ. И мнимых частей, то (3) равносильно системе равенств:

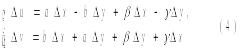
Равенства (3) означают, что функции u(x,y), v(x,y) удовлетворяют условию

∆u=B∆x+C∆y+β(∆x,∆y)∆x+γ(∆x,∆y)∆y, и следовательно, являются диффер-ми, т.к. коэффициент при ∆x и ∆у равны частным производным по х и у соответственно, то из (3) получаем:

a=∂u/∂x ; -b=∂u/∂y ; b=∂v/∂x ; a=∂v/∂y (4)

Отсюда и следует условие (1).

Достаточность. Предположим теперь, что функции u(x,y) и v(x,y) дифференцируемы в точке (х₀,у₀) и выполнены условия (1). Обозначая

a=∂u/∂x ; -b=∂u/∂y и применяя (1) придем к равенствам (4) .Из (4) и условия диффер-сти функций u(x,y) и v(x,y) имеем:

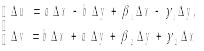
где β₁,β₂,γ₁,γ₂-функции стремящиеся к 0 при ∆x->0 ∆у->0 Отсюда

∆u+i∆v=(a+ib)(∆x+i∆y)+(β₁+iβ₂)∆x+(γ₁+iγ₂)∆у (5)

Определим функцию α(∆z) равенством:

α(∆z)=[(β₁+iβ₂)∆x+(γ₁+iγ₂)∆у]/∆z и положим А=a+ib, тогда (5) перепишется в виде ∆w=∆u+i∆v=A∆z+α(∆z)∆z, которое совпадает с (2). Для доказательства дифференцируемости f(z) осталось показать, что

lim α(∆z)=0 (при ∆z->0). Из равенства |∆z|=√(∆x)²+(∆y)² следует, что |∆х|≤|∆z|, |∆у|≤|∆z| поэтому |α(∆z)|

|α(∆z)|≤(|β₁+iβ₂||∆z|+|γ₁+iγ₂||∆z|/|∆z|)=|β₁+iβ₂|+|γ₁+iγ₂|

при ∆z->0, ∆х->0 и ∆у->0 ,а значит и функции β₁,β₂,γ₁,γ₂

стремятся к 0 , поэтому α(∆z)->0 при ∆z->0, что и требовалось доказать.