10,11.Непрерывность суммы степенного ряда. Интегрирование и дифференцирование степенного ряда.

Рассмотрим степенной ряд 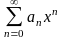, сходящийся в Тогда 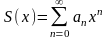, т.е. сумма ряда – функция.

1).S(x) непрерывная функция в любом замкнутом промежутке, принадлежащем интервалу

2) ряд (1) можно дифференцировать почленно внутри интервала сходимости, при этом радиус сходимости не изменяется

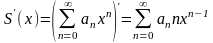
3) ряд (1) можно интегрировать почленно по любому промежутку (a,b), лежащему в интервале сходимости, при этом радиус сходимости полученного ряда остается прежним.

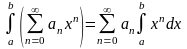
12,13. Степенной ряд. Теорема Абеля. Область сходимости. Равномерная сходимость.

Функциональный ряд вида (1) или (2)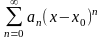 , называется степенным рядом.

(1) сходится при х=0.

Т.Абеля:

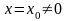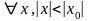1)Пусть (1) сходится абс при Тогда он сходится для . 2)Пусть (1) расходится при 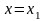Тогда он расходится для

Док-во: 1)Пусть (1) сходится при 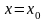, т.е.

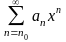сходится => по необходимому признаку

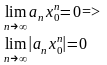
=> последовательность 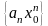сходящаяся. => она ограничена, т.е.

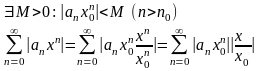
Пусть

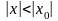
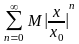Это геом. прогрессия. Она сходится, т.к.

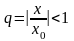
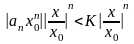Для достаточно больших n. По 1 признаку сравнения 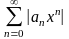сходится для => (1) сходится для .

2)Пусть (1) в точке расходится. Докажем, что для он также расходится.

Предположим противное: (1) сходится в 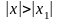Тогда по 1-ой части теоремы он должен сходится и в точке , что неверно => (1) расходится для .

Степенной ряд сходится на интервале (-R;R) с центром в точке. Число R- радиус сходимости степенного ряда может быть вычислено по формулам

, или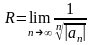 . Степенной ряд сходится равномерно на любом отрезке, целиком лежащем внутри интервала сходимости. Сходимость степенного ряда на границах интервала сходимости необходимо исследовать специально для конкретного ряда.

14. Ряд Тейлора. Разложение функции в ряд Тейлора. Необходимое и достаточное условие разложения в ряд Тейлора. Примеры разложения основных функций в ряд Тейлора.

Разложение функций в ряд Тейлора. При исследовании свойств бесконечно дифференцируемых функций изучают их степенные ряды ряды Тейлора. Пусть функция f(x) определена в некоторой окрестности точки x₀ и имеет в этой точке производные всех порядков. Ряд

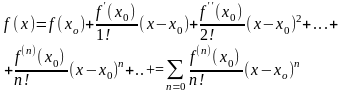
называется рядом Тейлора для функции f(x) в точке x₀. При x₀ =0 такой ряд называют также рядом Маклорена. Функция f(x) может быть разложена в степенной ряд на интервале, если существует степенной ряд, сходящийся к f(x) на этом интервале. Если функция раскладывается в степенной ряд в некоторой окрестности точки x₀, то это ряд Тейлора.

Необх.и дост. условие разложимости: если ф-я разложима в ряд Тейлора в окрестности U(х₀,) необх. и дост., чтобы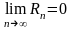 R_n – остаточный член ряда Тейлора

Дост. условие разложимости:

Если производные всех порядков ф-и f(x) ограничены в некоторой окрестности точки x=x₀ одним и тем же числом M>0, то ф-я f(x) разложима в этой окрестности в ряд Тейлора.

то выполняется

Разложение основных элементарных функций

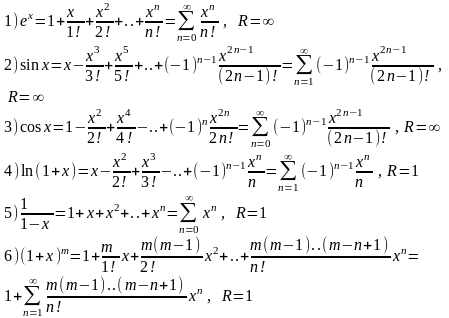
15,16. Ряд Фурье для тригонометрических функций.Теорема Дирихле

f(x)= 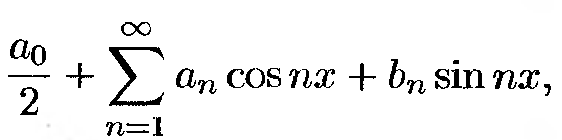(4)

где

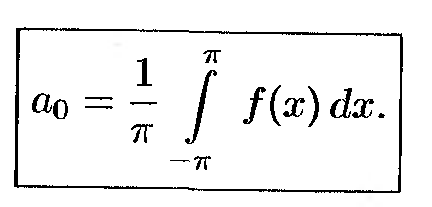
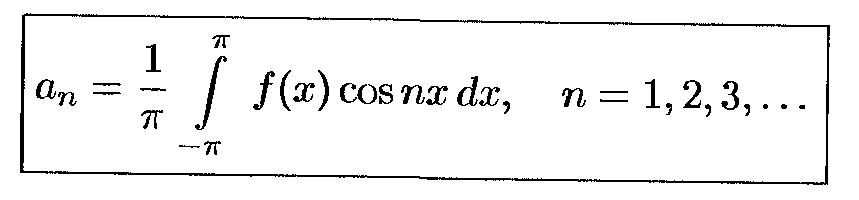
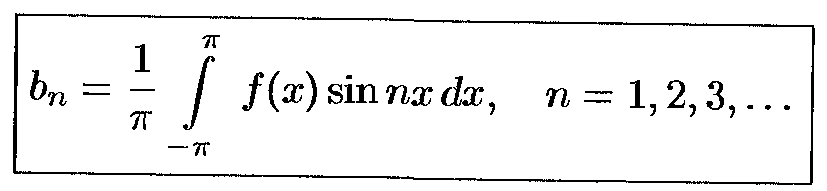
Определение: Функция наз-ся кусочно-непрерывной на данном отрезке, если этот отрезок можно разбить на конечное число интегралов, в каждом из которых функция непрерывна.

Т-ма Дирихле: Пусть f(x)

1)определена для всех х[-,]

2)кусочно-непрерывная на [-,]

3)кусочно-монотонная на [-,]

4)ограничена на [-,], тогда она разложима в тригонометрический ряд Фурье (4). Если точка х[-,] и в этой точки f(x) непрерывна, то сумма ряда

S(x)=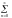 (a_ncos(nx)+b_nsin(nx))=f(x). Если точка х - точка разрыва, скачок, то S(x)=^1/2 [f(x-0)+f(x+0)]

S(-)=S()=^1/2 [f(+0)+f(-0)]

Замечания: 1)поведение функции f за пределами [-,] может в корне отличаться от значения S.

2)если мы хотим разложить f на всей действительной оси, то соглас- но (4) мы должны продол- жить периодическим образом с периодом 2.