6. 3. Метод Лагранжа

Чтобы применить метод исключения переменных, нужно построить функ- цию φ(х) = f (х , y₁(x), y₂(x), …, y_m(x)), а это возможно только тогда, когда най- дено решение y₁(x), y₂(x),…, y_m(x) системы (3). Однако, найти его удаётся далеко не всегда. Метод Лагранжа обходит указанное препятствие, поскольку, хотя метод и опирается на существование решения y₁(x), y₂(x), …, y_m(x), он не требует, чтобы решение было найдено.

Пусть функция f (х,у) непрерывно дифференцируема на множестве Х , а u₀ = (х₀ ,у₀) является точкой условного экстремума этой функции при нали- чии уравнений связи (3), и пусть система (3) и точка u₀ удовлетворяют требо- ваниям условия теоремы 1. Тогда х₀ – точка свободного экстремума функции φ(х) = f (х , y₁(x), y₂(x), …, y_m(x)) , где y₁(x), y₂(x),…, y_m(x) – решение системы (3) в некоторой окрестности U(δ). Очевидно, φ(х) дифференцируема в х₀ , значит, х₀ – стационарная точка этой функции; поэтому (см. замечание, п.2, § 5) для любого.

Обозначим: φ_k(x) =F_k(x, y₁(x), y₂(x), … , y_m(x)), k = 1,2, …,m . Так как y₁(x), y₂(x),…, y_m(x) – решение системы (3), то φ_k(x) ≡ 0 в U(δ), k = 1,2, …,m; следовательно при любых .

Составим выражение:

+ λ + λ +…+ λ , (5) где λ, λ , …, λ - некоторые числа ( их называют множителями Лагранжа). Очевидно, сумма (5) равна нулю при любом .

В силу инвариантности формы первого дифференциала имеем:

,

где dy_i = , i= 1,2,…,m. Подставим эти выражения в (5):

+ =

= +

+

+λ( +

+ +λ(+

+

………………………………………………………………………………….. +λ(+

+=

=…

… + +…

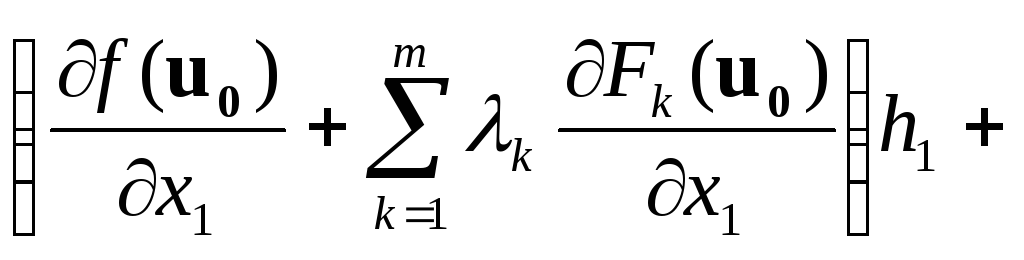
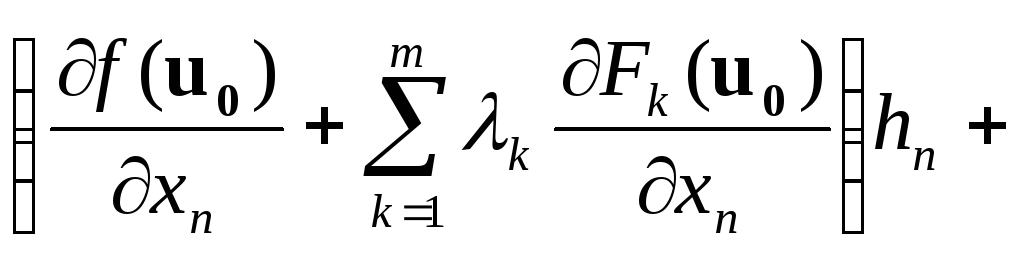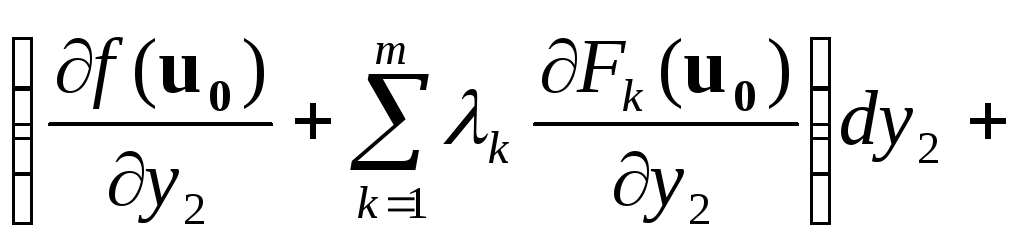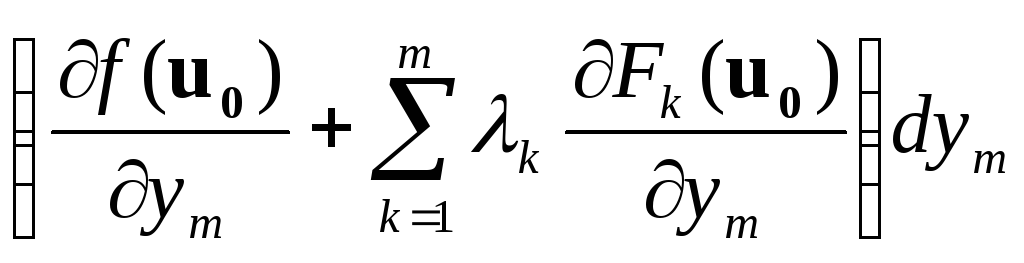… + . На выбор чисел λ, λ , …, λ не были наложены какие –либо ограничения. Потребуем теперь, чтобы набор λ, λ , …, λ удовлетворял системе линей- ных алгебраических уравнений, которую мы получим приравняв нулю выра- жения при дифференциалах dy₁, dy₂, …,dy_m:

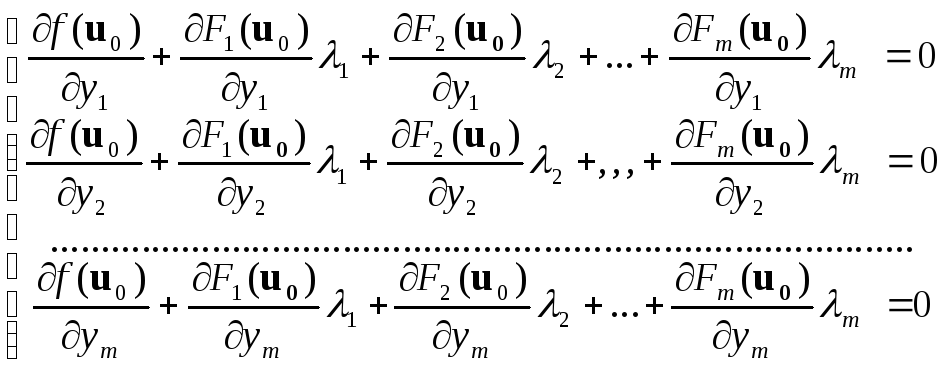(6) Определитель этой системы представляет собой транспонированный якобиан функций , 1,2, …, m, по переменным у₁,у₂, …,у_m в точке u₀; значит, он отличен от нуля; поэтому система имеет единственное решение – обозна- чим его через λ, λ , …, λ. Подставив эти числа в (5), для любых , будем иметь:

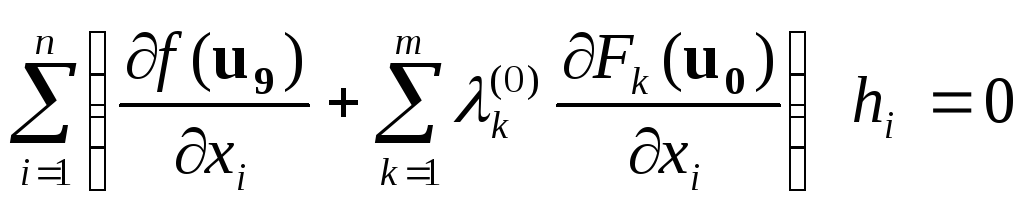+ = , Так как здесь произвольны, то в каждом слагаемом последней суммы выражение в скобках равно нулю:

(7)

……………………………………………

Итак, координаты точки условного экстремума u₀ и множители Лагранжа λ, λ , …, λ удовлетворяют системе равенств (3), (6) и (7) – всего n+2m равенств.

Пусть u , u = ( х₁,х₂, … ,х_n, у₁,у₂, … ,у_m) , а λ, λ = (λ₁,λ₂,…,λ_m). Поло- жим:

L(u,λ) = f(u) + . L(u,λ) есть функция n + 2m аргументов х₁,х₂, … ,х_n, у₁,у₂, …,у_m, λ₁,λ₂,…,λ_m. Её называют вспомогательной функцией Лагранжа. Приравняв нулю частные производные этой функции по всем её аргументам и сопоставив полученную в результате систему n + 2m уравнений с равенствами (3), (6) и (7), приходим к заключению: если u₀ является точкой условного экстремума функции f (х,у) при наличии уравнений связи (3), то точка (u₀, λ, λ,…, λ), где λ, λ, …, λ найдены из системы (6), является стационарной точкой функции Лагранжа L(u,λ).

Итак, пусть функция f (х,у) непрерывно дифференцируема в некоторой окрестности точки u₀ =(х₀ ,у₀) и пусть система (3) и точка u₀ удовлетворяют требованиям условия теоремы 1. Если u₀ является точкой условного экстре- мума, то среди стационарных точек функции Лагранжа имеется такая, что набор её первых n + m координат есть координаты точки u₀.

Пусть найдены все стационарные точки функции Лагранжа. Набор пер- вых n + m координат каждой из них есть координаты точки, подозрительной на условный экстремум функции f (х,у) – функция f (х,у) может иметь услов- ный экстремум только в таких точках. Однако, вообще говоря, не всякая по- дозрительная точка оказывается точкой условного экстремума на самом деле. Чтобы выяснить, имеется ли в данной подозрительной точке условный экст- ремум нужно её исследовать с помощью достаточного признака.

Пусть (u₀, λ, λ,…, λ) – стационарная точка функции Лагранжа. Тог- да u₀– точка, подозрительная на условный экстремум. Рассмотрим систему уравнений:

(8)

Левые части этих уравнений представляют собой дифференциалы функ- ций F_k(u) = F_k(u₁,u₂, … ,u_n+m), k = 1,2, …,m, в точке u₀ . Относительно диффе- ренциалов h_j = du_j, j = 1,2,…,n+m, это однородная система m линейных алге-браических уравнений . Так как в точке u₀ якобиан функций F_k(u) = F_k(u₁,u₂, … ,u_n+m), k = 1,2, …,m, по переменным у₁= u_n+1, у₂ =u_n+2, … , у_m= u_n+m отличен от нуля, то ранг матрицы системы (8) равен m ; следовательно, множество её решений есть линейное подпространство в размерности n. Обозначим это подпространство через H .

Допустим, что функции F_k(u), k = 1,2, …,m, и f (u) дважды непрерывно дифференцируемы в некоторой окрестности точки u₀. Тогда и функция L(u,λ₀) = f(u) + обладает таким свойством. Запишем её второй дифференциал в точке . u₀: . Здесь h = (h₁,h₂ ,… ….,h_n+m). Дифференциал представляет собой квадратичную форму от n+m переменных h₁,h₂ ,… ,h_n+m. Мы будем говорить, что эта форма положи- тельно определена ( отрицательно определена) на множестве H, если для лю- бого ненулевого вектора h, принадлежащего множеству H, справедливо > 0 (< 0). Мы назовем форму знакопеременной на мно- жестве H, если в этом множестве существуют векторы h₁ и h₂ такие, что и .

Теорема 3. ( Достаточный признак условного экстремума)

Пусть (u₀, λ, λ,…, λ) = (u₀,λ₀) – стационарная точка функции Лагран- жа L(u,λ) = f(u) + , и пусть функции f (u) и F_k(u), k = 1,2, …,m, дважды непрерывно дифференцируемы в некоторой окрестности точки u₀. Если форма положительно определена (отрица- тельно определена) на множестве H, то u₀ является точкой строгого условно- го минимума (строгого условного максимума) функции f при наличии урав- нений связи (2). Если же на есть знакопеременная форма на множест- ве H, то u₀ не является точкой условного экстремума функции f .

Доказательство этой теоремы можно найти в [1].

Пример 3. Изложим решение задачи примера 2 методом Лагранжа. Име- ем: , . В отличие от приме- ра 2 положим . Этот выбор обьясняется тем, что расстояние между точкой параболы и точкой прямой и квадрат этого расстояния достигают своей наименьшей вели- чины одновременно, т.е. для одной и той же пары точек, а производные от проще, чем производные от . Составим вспомогательную функцию Лагранжа:

+

Составим систему уравнений, приравняв нулю частные производные функции :

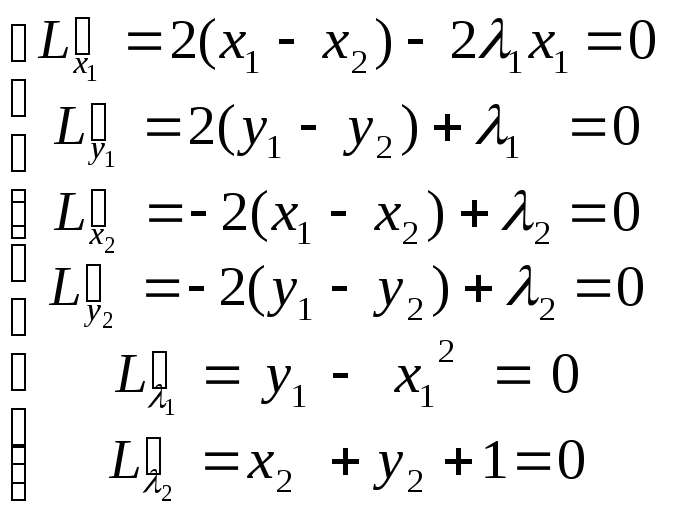
Из третьего и четвёртого уравнений:. Отсюда и из вто- рого уравнения: , значит, . Подставив в первое уравнение, получим: . Значит либо 0 , либо . Если допустить 0, то тогда и 0; отсюда: , т.е. точки и совпадают, а это невозможно, так как парабола и прямая не пересе- каются. Следовательно, . Отсюда и из пятого уравнения: . Подставив найденные значения х₁ и у₁ в равенство , получим: . Отсюда и из шестого уравнения найдем: . Теперь найдём и : . Таким образом, найдена стационарная точка функции Лагранжа:

. Значит, u₀- единственная подозрительная на условный экстремум точка; как и следовало ожидать, она совпала с точкой , найденной в примере 2. Исследуем u₀ с помощью достаточного признака. Запишем дифференциал второго порядка функции в точке u₀:

. Дифференцируя уравнения связи в точке u₀, найдём: . Введя эти значения и в выражение , получим: = . Отсюда ясно, что если хотя бы один из дифференциалов и отличен от нуля, то > 0. Следовательно, u₀ - точка строгого условного минимума.

Впрочем, вывод о характере u₀ можно было бы сделать и не подвергая её исследованию. Из геометрического содержания задачи очевидно, что точка условного минимума существует. Она обязана быть точкой, подозрительной на условный экстремум. Но имеется только одна подозрительная точка - u₀ . Значит, u₀ и есть точка условного минимума.