§ 6. Условный экстремум

6.1. Основные определения

Пусть n и m – заданные натуральные числа, Х – открытое множество, лежащее в , F_k(u) = F_k(u₁,u₂, … ,u_n+m), k = 1,2, …,m, - функции, определен- ные на Х, D – множество точек u = (u₁,u₂, … ,u_n+m), координаты которых удовлетворяют системе уравнений

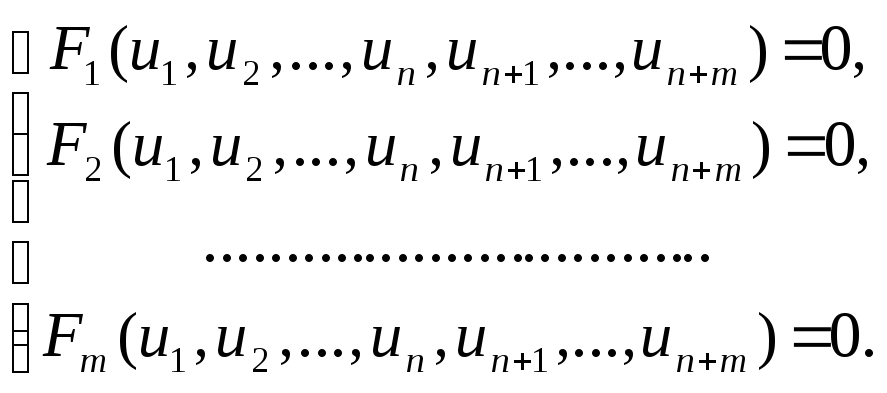(1) Так как количество уравнений в системе (1) меньше числа координат, то, во- обще говоря, D – бесконечное множество.

Пусть f(u) = f(u₁,u₂, … ,u_n+m) – некоторая функция, определенная на Х, а u₀ – некоторая точка множества D.

Определение 1. u₀ D, назовем точкой условного минимума (условно- го максимума) функции f при наличии уравнений связи (1), если существует δ > 0 такое, что для всех u, принадлежащих пересечению δ –окрестности ( δ) точки u₀ с множеством D, справедливо неравенство f(u) ≥f(u₀) ( f(u) ≤ f(u₀) ).

Определение 2. u₀ D, назовем точкой строгого условного минимума (строгого условного максимума) функции f при наличии уравнений связи (1), если существует δ > 0 такое, что для всех u, принадлежащих пересече- нию проколотой δ – окрестности ( δ) точки u₀ с множеством D, справед- ливо строгое неравенство f(u) >f(u₀) ( f(u) < f(u₀)).

Точки условного минимума и условного максимума ( строгого услов- ного минимума и строгого условного максимума ) функции f называют точ- ками условного экстремума (строгого условного экстремума ) этой функции. Отличие точки свободного экстремума функции от точки её условного экст- ремума состоит в том, что в первом случае значение f(u₀) сравнивается со значениями функции f во всех точках δ – окрестности ( δ), а во втором случае только со значениями f в тех точках этой окрестности, координаты которых удовлетворяют системе (1). Точка условного экстремума функции может не быть точкой её свободного экстремума.

Пример 1. Рассмотрим задачу: пусть Δ – прямая в пространстве, не проходящая через начало координат; на Δ найти точку М₀, ближайшую к на-чалу координат. Задача, очевидно, имеет единственное решение: М₀ есть основание перпендикуляра, опущенного из начала координат на Δ (рис.2). Точку М₀ можно рассматривать как точку условного минимума функции. Действительно, запишем уравнение прямой Δ в виде системы уравнений двух плоскостей (Δ есть линия пересечения этих плоскостей) :

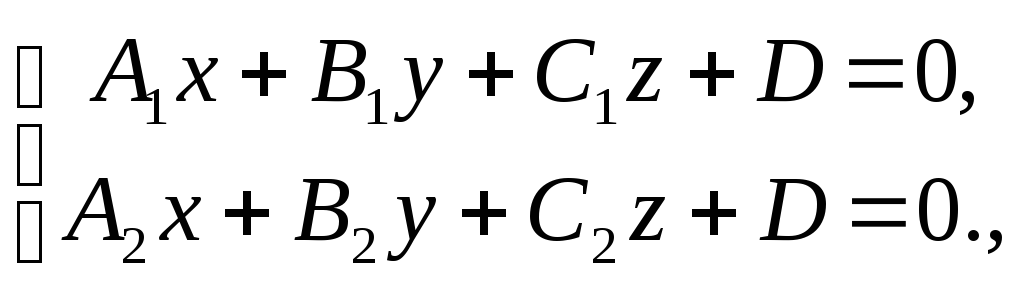(2) и положим f (x,y,z) = , т.е. значение функции f в точке М (x,y,z) равно расстоянию между этой точкой и началом координат. М₀ (x₀,y₀,z₀) явля- ется точкой условного минимума функции f при наличии уравнений связи (2). Отметим, что при этом М₀ не является точкой свободного экстремума функции f , так как в любой окрестности имеются точки, расположенные и ближе, и дальше от начала координат, чем М₀ .

Пусть требуется найти точки условного экстремума функции f при наличии уравнений связи (1). Ниже изложены два метода решения такой задачи – метод исключения переменных и метод неопределенных множите- лей Лагранжа.

6.2. Метод исключения переменных

Приведем формулировку теоремы о существовании решения системы уравнений (см. стр.38) в несколько изменённом виде. Обозначим первые n координат точки u через х₁,х₂, …,х _n , а последующие m её координат – через у₁,у₂, …,у_m: u = (u₁,u₂, … ,u_n+m) = (х₁,х₂, … ,х_n, у₁,у₂, …,у_m ) = (х,у), где х = (х₁,х₂, … ,х_n) , у = (у₁,у₂, …,у_m). Тогда система (1) примет вид:

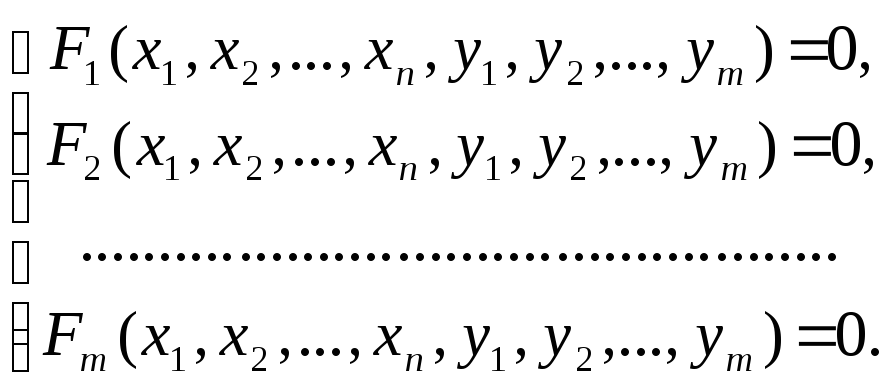(3)

Теорема 1. Пусть функции 1,2, …, m, непрерывно диффе- ренцируемы в некоторой окрестности точки u₀ = (х₀ ,у₀), где х₀ =( х₁₀,х₂₀, … ,х_n0) , у₀ = (у₁₀,у₂₀, …,у_m0), и удовлетворяют следующим требованиям:

1. F_k(u₀) = 0, k = 1,2, …,m, ( т.е. u₀ D);

2. якобиан системы функций 1,2, …, m, по переменным у₁,у₂, …,у_m, отличен в точке u₀ от нуля .

Тогда существуют δ >0 и ε >0, а также единственный набор функций y₁(x),y₂(x), … ,y_m(x), определенных в δ - окрестности U (δ) точки х₀ , таких, что

1) F_k(x,y₁(x),y₂(x), … ,y_m(x)) ≡ 0 в U (δ), k = 1,2, …,m ( т.е. набор y_i(x), i =1,2,…,m, есть решение системы (3) на множестве U(δ)) ;

2) при всяком x U (δ) точка у = (y₁(x),y₂(x), … ,y_m(x)) принадлежит ε -окрестности U( ε) точки у₀ , причём y_i(x₀) = y_i0 , i =1,2,…,m;

3) функции y_i(x), i =1,2,…,m, непрерывно дифференцируемы на мно- жестве U(δ).

Замечание. Обозначим:

,

.

- окрестность точки u₀ , т.е. открытое множество,содержащее u₀ . Так как при всяком x U (δ) точка у =(y₁(x), y₂(x), … ,y_m(x)) принадлежит ε –окрестности U( ε), то принадлежит и представляет собой совокуп- ность всех тех точек окрестности , координаты которых удовлетворяют уравнениям (3). Подчеркнём , что при каждом x U (δ) в окрестности имеется и при том только одна точка u множества D такая, что её первые n координат образуют вектор x , а именно, это принадлежащая точка u = =(x,y₁(x),y₂(x), … ,y_m(x)) .

Пусть для системы (3) и точки u₀ = (х₀ ,у₀) выполнены условия теоремы 1, а y₁(x),y₂(x), … ,y_m(x) - решение системы на множестве U( δ). Пусть, да- лее, f(х₁,х₂, … ,х_n, у₁,у₂, …,у_m ) = f (х,у)) – некоторая функция, определенная на множестве Х. Обозначим: φ(х) = f (х , y₁(x), y₂(x), …, y_m(x) ). Из теоремы 1 и замечания к ней вытекает: u₀ являетсяч точкой условного минимума (точкой условного максимума, не является точкой условного экстремума) функции f при наличии уравнений связи (3) тогда и только тогда, когда х₀ является точ- кой свободного минимума (точкой свободного максимума, не является точ- кой свободного экстремума) функции φ . Это позволяет свести задачу об ус- ловном экстремуме функции f к задаче о свободном экстремуме функции φ.

Пример 2. Пусть требуется определить расстояние между плоскими кривыми и ( рис.3.) , т.е. требуется найти наименьшее рас- стояние между двумя точками, одна из которых лежит на параболе , а другая – на прямой .

Пусть M(х₁,у₁) – произвольная точка параболы, а N(х₂,у₂)- произвольная точка на прямой. Обозначим через f(х₁, х₂,у₁, у₂) длину отрезка M N :

f(х₁, х₂,у₁, у₂) =

П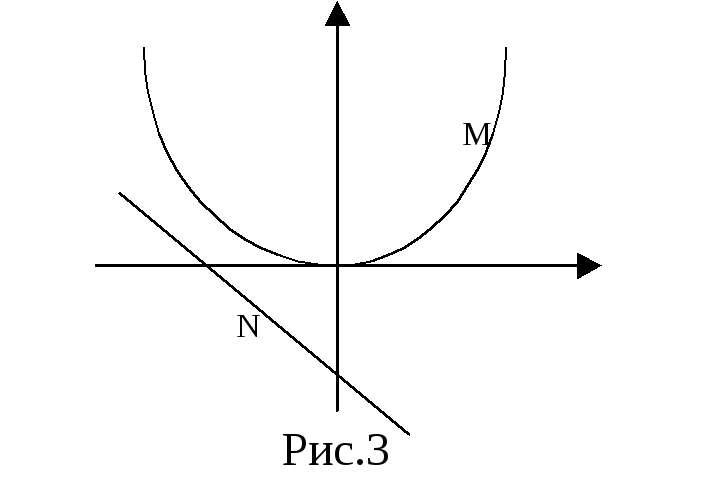оставленная задача сводится к отыска- нию наименьшего значения функции f(х₁, х₂,у₁, у₂) при условии, что её аргу- менты связаны уравнениями

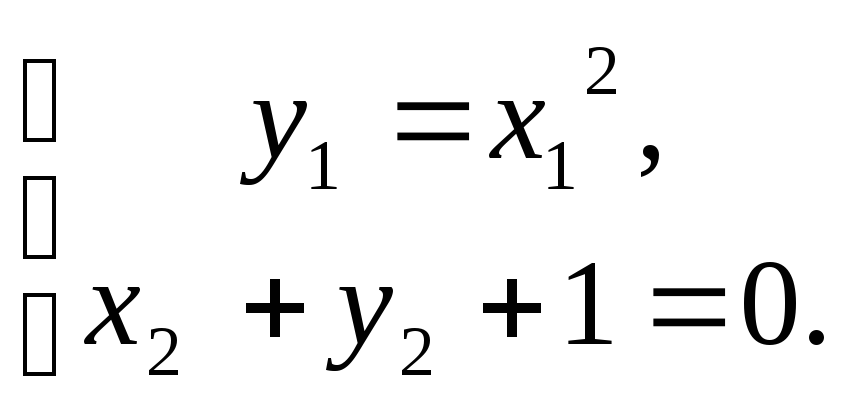(4)

Нетрудно найти решение этой системы: . Отсюда получим:

. Функция определена при любых вещественных х₁ и х₂. Найдём её ста- ционарные точки, для чего приравняем нулю частные производные:

Эта система равносильна системе

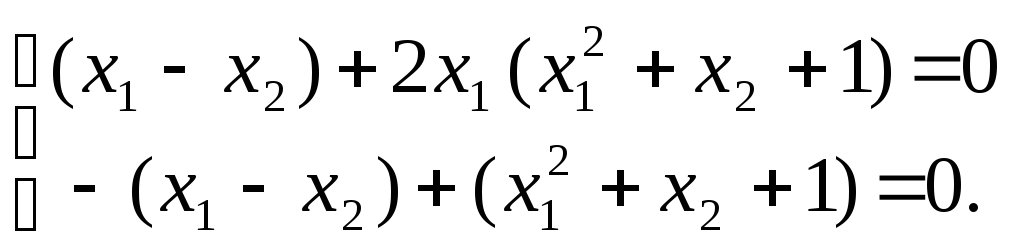
Из второго уравнения: . Подставив в первое уравнение, по- лучим: (х₁ -х₂)(2х₁+1)=0. Следовательно, либо х₁ = х₂, либо х₁. Положив во втором уравнении системы х₁ = х₂, получим уравнение , которое не имеет вещественных корней. Значит, х₁. Подставив это зна- чение во второе уравнение системы, найдём: х₂. Таким образом, для функции имеется только одна подозрительная на экстремум точка – точка . С помощью теоремы 3, п.3, § 5, нетрудно убедиться, что это точка строгого минимума функции . Из уравнений связи при х₁ и х₂ следует: . Значит, u₀ = - это единственная точка строгого условного минимума функции f(х₁, х₂,у₁, у₂), a f (u₀) есть наименьшее значение этой функции при наличии уравнений связи (4). Расстояние между параболой и прямой равно рассто- янию между точкой параболы и точкой прямой .