
- •§ 1. Пространство и его подмножества
- •§ 2. Функция n переменных, ее предел и непрервность
- •§ 3. Частные производные и дифференциал функции n, n2,
- •Обозначают введенную этим определением частную производную символами fх′(m0) или fх′(x0,y0) , а также
- •§ 4. Неявные функции.
- •§ 5. Свободный экстремум функции нескольких переменных
- •Пусть , а - любое, удовлетворяющее условиям . Взяв , удовлетворяющее указанным условиям, выберем для этого число такое, что и обозначим: . Имеем: , причём ;
- •§ 6. Условный экстремум
- •6. 3. Метод Лагранжа
- •В силу инвариантности формы первого дифференциала имеем:
- •Литература
- •§ 1. Пространство и его подмножества
- •Пространство …………………………. 3
- •§ 2. Функция n переменных, её предел и непрерывность
- •§ 3. Частные производные и дифференциалы
- •§ 4. Неявные функции
- •§ 5. Свободный экстремум функции нескольких переменных
- •§ 6. Условный экстремум
§ 5. Свободный экстремум функции нескольких переменных
5.1. Основные определения.
Пусть
Х
- открытое множество в пространстве
![]() ,
х0
= (
,
х0
= (![]() )
- - точка, принадлежащая Х,
f
(x)
= f
(x1,x2
, …, xn)
– функция, определённая на множестве
Х.
)
- - точка, принадлежащая Х,
f
(x)
= f
(x1,x2
, …, xn)
– функция, определённая на множестве
Х.
Определение
1. х0
назовём
точкой минимума (точкой максимума) фун-
кции f
, если можно
указать δ
>0 такoe,
что при всяком х,
принадлежащем
δ-
-окрестности
![]() (
δ),
справедливо неравенство f
(x)
≥ f
(x0)
(f
(x)
≤
f
(x0)
).
(
δ),
справедливо неравенство f
(x)
≥ f
(x0)
(f
(x)
≤
f
(x0)
).
Определение
2. х0
назовём точкой строгого минимума (
точкой строгого максимума) функции f,
если если можно указать δ
>0 такoe,
что при всяком х,
принадлежащем
проколотой δ-окрестности
![]() (
δ),
справедливо строгое неравенство f
(x)
> f
(x0)
(f
(x)
< f
(x0)
).
(
δ),
справедливо строгое неравенство f
(x)
> f
(x0)
(f
(x)
< f
(x0)
).
Точки максимума и минимума функции называют точками её экстре- мума; точки строгого максимума и строгого минимума – точками строгого экстремума функции.
Пример
1. Начало
координат, точка О
(0,0) является
для каждой из функций двух переменных
f1(x,y)
=
![]()
![]() ,
,
![]()
![]() точкой
строгого экстремума: для первой и третьей
функций точ- кой строгого минимума, а
для второй - точкой строгого максимума.
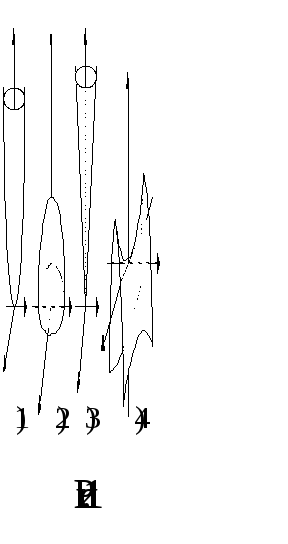
Графики этих функций (параболоид,
полусфера, конус) изображены на рис.
11),12)и
13).
точкой
строгого экстремума: для первой и третьей
функций точ- кой строгого минимума, а
для второй - точкой строгого максимума.
Графики этих функций (параболоид,
полусфера, конус) изображены на рис.
11),12)и
13).
Ниже
мы рассматриваем следующую задачу:
пусть функция f
опреде- лена
на некотором открытом множестве Х
![]() ;
требуется выяснить, имеет ли f
на этом
множестве точки экстремума; в случае
наличия таких точек классифицировать
их ( максимум или минимум).
;
требуется выяснить, имеет ли f
на этом
множестве точки экстремума; в случае
наличия таких точек классифицировать
их ( максимум или минимум).
5.2. Необходимые условия экстремума.
Решение поставленной выше задачи начинают с отыскания точек, в которых выполнены необходимые условия экстремума.
Теорема
1. Пусть
х0
= (![]()
![]() )
является точкой экстремума функции f
(x)
= f
(x1,x2
, …, xn).
Если f
дифференцируема
в х0
, то
в точке х0
все
частные производные первого порядка
функции
f
равны нулю.
)
является точкой экстремума функции f
(x)
= f
(x1,x2
, …, xn).
Если f
дифференцируема
в х0
, то
в точке х0
все
частные производные первого порядка
функции
f
равны нулю.
►
Функция
f
дифференцируема в х0
,
значит (см. [3], стр.18), в точке х0
существуют
частные производные по всем аргументам
функции f.
Докажем
равенство нулю частной производной по
аргументу х1
:![]() .
По опреде- лению ( [3], стр.18)
.
По опреде- лению ( [3], стр.18)
![]() =
=
![]() (
(![]() ),
где
),
где
![]() f
(t,
f
(t,
![]()
![]() ).
Функция f
оп- ределена
в окрестности
х0
и имеет в этой точке экстремум; поэтому
функ- ция
).
Функция f
оп- ределена
в окрестности
х0
и имеет в этой точке экстремум; поэтому
функ- ция
![]() определена в окрестности точки
определена в окрестности точки
![]() ,
т.е. на некотором интервале чис- ловой
оси, содержащем число
,
т.е. на некотором интервале чис- ловой
оси, содержащем число
![]() ,
причем
,
причем
![]() является точкой экстремума функции
является точкой экстремума функции
![]() .
В силу теоремы Ферма ([2], стр. 19 )
.
В силу теоремы Ферма ([2], стр. 19 )
![]() (
(![]() )
= 0, т.е.,
)
= 0, т.е.,
![]() .
Аналогично докажем равенство нулю
частных производных и по другим
аргументам. ◄
.
Аналогично докажем равенство нулю
частных производных и по другим
аргументам. ◄
Следствие.
Пусть функция
f
(x)
дифференцируема в точке х0
![]() .
Если хотя
бы одна из частных производных
.
Если хотя
бы одна из частных производных
![]() отлична
от нуля, х0
заведомо не является точкой экстремума,.
отлична
от нуля, х0
заведомо не является точкой экстремума,.
Опрееделение
3. Точку х0
![]() назовём
стационарной
точкой функции
f
, если f
дифференцируема в х0
, а все её
частные производные первого порядка
в этой
точке f
равны нулю.
назовём
стационарной
точкой функции
f
, если f
дифференцируема в х0
, а все её
частные производные первого порядка
в этой
точке f
равны нулю.
Замечание
. Пусть
функция f
(x)
= f
(x1,x2
, …, xn)
дифференцируема в точке х0,
х0
= (
![]() ).
Точка х0
является
стационарной точкой функ- ции f
тогда и
только тогда, когда первый дифференциал
).
Точка х0
является
стационарной точкой функ- ции f
тогда и
только тогда, когда первый дифференциал
![]() тождествен- но равен нулю (т.е.
тождествен- но равен нулю (т.е.
![]() для любого
для любого![]()
![]() ).
).
►Пусть
х0
является
стационарной точкой, т.е.
![]() ,
,![]() ;
тогда при всяком
;
тогда при всяком
![]() имеем:
имеем:
![]()
![]() С другой сто- роны, пусть
С другой сто- роны, пусть
![]() при всяком
при всяком
![]() .
Положим
.
Положим
![]() .
Для этого вектора имеем:
.
Для этого вектора имеем:
![]()
![]()
![]() .
Положив
.
Положив
![]() получим:
получим:
![]()
![]()
![]() .
Аналогично докажем равенство нулю
частных производных и по другим аргументам
функции. ◄
.
Аналогично докажем равенство нулю
частных производных и по другим аргументам
функции. ◄
Пусть
функция f
(x)
определена
на некотором открытом множестве Х,
Х
![]() .
Точку х0
.
Точку х0
![]() назовем
точкой,
подозрительной на экстремум функции
f
, если либо
1) х0
является
стационарной точкой этой функции, либо
2) f
не-
дифференцируема в х0
.
Из теоремы
1. вытекает, что только в таких точках
функция может иметь экстремум. Но не
всегда подозрительная на экстремум
точка оказывается точкой экстремума
на самом деле.
назовем
точкой,
подозрительной на экстремум функции
f
, если либо
1) х0
является
стационарной точкой этой функции, либо
2) f
не-
дифференцируема в х0
.
Из теоремы
1. вытекает, что только в таких точках
функция может иметь экстремум. Но не
всегда подозрительная на экстремум
точка оказывается точкой экстремума
на самом деле.
Пример
2. Легко
проверить, что для функции
![]() начало координат О
(0,0) есть её
стационарная точка. Однако, точкой
экстремума она не является:
начало координат О
(0,0) есть её
стационарная точка. Однако, точкой
экстремума она не является:
![]() ,
а в любой окрестности точки О(0,0)
имеются как точки, в которых значения
функции положительны, так и точки, где
функ- ция принимает отрицательные
значения; это становится достаточно
очевид- ным при взгляде на график функции
– гиперболический параболоид (рис.
14)).
,
а в любой окрестности точки О(0,0)
имеются как точки, в которых значения
функции положительны, так и точки, где
функ- ция принимает отрицательные
значения; это становится достаточно
очевид- ным при взгляде на график функции
– гиперболический параболоид (рис.
14)).
5.3. Достаточные условия экстремума.
Исследование функции на экстремум начинают с отыскания точек, по- дозрительных на экстремум – только в таких точках функция может иметь экстремум. Является ли подозрительная точка точкой экстремума на самом деле, выясняют с помощью достаточных признаков. Теорема 2 - один из та- ких признаков; им пользуются, исследуя стационарные точки. Предвари- тельно сделаем ряд замечаний.
Согласно
определению 1 х0
![]() является точкой минимума (точкой
максимума) функции f
, если можно
указать δ
>0 такое,
что при всех х
является точкой минимума (точкой
максимума) функции f
, если можно
указать δ
>0 такое,
что при всех х![]()
![]()
![]() (
δ),
справедливо неравенство f
(x)
- f
(x0)
≥0 (f
(x)
- f
(x0)
≤0 ) . Поло- жим h
= x
– x0;
тогда x
=x0
+h
и
(
δ),
справедливо неравенство f
(x)
- f
(x0)
≥0 (f
(x)
- f
(x0)
≤0 ) . Поло- жим h
= x
– x0;
тогда x
=x0
+h
и
![]()
![]()
![]() .Заме-
тим: (
.Заме-
тим: (![]() )
)
![]() ( ||h||
< δ
). Теперь нетрудно заключить:
( ||h||
< δ
). Теперь нетрудно заключить:
I.
x0
является
точкой минимума (максимума) функции f
тогда и
только тогда, когда можно указать
δ
>0 такое,
что при всех h
, удовлетворяющих условию ||h||
< δ
, справедливо неравенство
![]() ≥
0 (
≥
0 (![]() ≤
0).
≤
0).
Из определения 2 аналогично следует:
II.
х0
является
точкой строгого минимума (строгого
максимума) функ- ции f
тогда и
только тогда, когда можно указать
δ
>0 такое,
что при всех h
, удовлетворяющих условию 0 < ||h||
< δ
, справедливо строгое неравенство
![]() >
0 (
>
0 (![]() <
0).
<
0).
Справедливо также утверждение:
III.
Если при всяком δ
>0 можно
указать h1
и h2
такие, что
||h1||
< δ,
||h2||
< δ,
а соответствующие приращения
![]() и
и
![]() отличны
от нуля и имеют противоположные знаки,
то х0
не является
точкой экстремума функции f.
отличны
от нуля и имеют противоположные знаки,
то х0
не является
точкой экстремума функции f.
►
Действительно,
в этом случае нельзя указать δ
>0 так, чтобы
при всех h,
удовлетворяющих требованию ||h||
< δ
, соответствующие приращения
![]() были
бы числами одного знака. В силу утверждения
I.
х0
не
может
быть
ни точкой минимума, ни точкой максимума.
◄
были
бы числами одного знака. В силу утверждения
I.
х0
не
может
быть
ни точкой минимума, ни точкой максимума.
◄
Пусть
функция f
дважды
дифференцируема
в точке x0
.Запишем диффе- ренциал второго порядка
![]() функции
f
в точке x0:
функции
f
в точке x0:
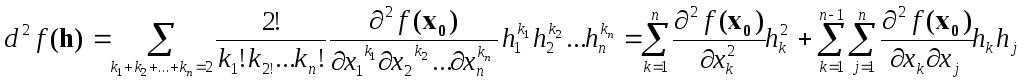 ,
где h
= (h1,h2.
…,hn).
Это выражение представляет собой
квадратичную фор- му от n
переменных
h1,h2,…,hn.
Напомним, что квадратичнная форма может
быть либо знакоопределенной, положительно
или отрицательно, либо квази-
знакоопределенной, либо знакопеременной
([4],стр. 8).
,
где h
= (h1,h2.
…,hn).
Это выражение представляет собой
квадратичную фор- му от n
переменных
h1,h2,…,hn.
Напомним, что квадратичнная форма может
быть либо знакоопределенной, положительно
или отрицательно, либо квази-
знакоопределенной, либо знакопеременной
([4],стр. 8).
Теорема 2. (Достаточный признак экстремума) Пусть х0 является стационарной точкой функции f и пусть f дважды дифференцируема в неко- торой окрестности этой точки. Тогда:
-
если
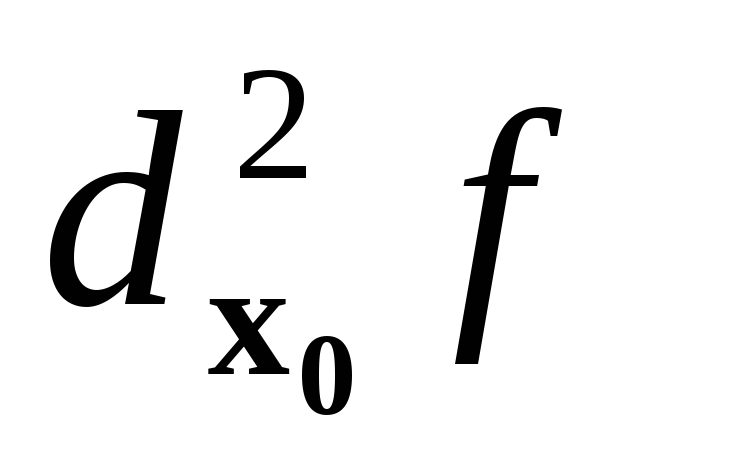 -
положительно определенная квадратичная
форма, то х0
является
точкой строгого минимума функции f
;
-
положительно определенная квадратичная
форма, то х0
является
точкой строгого минимума функции f
; -
если
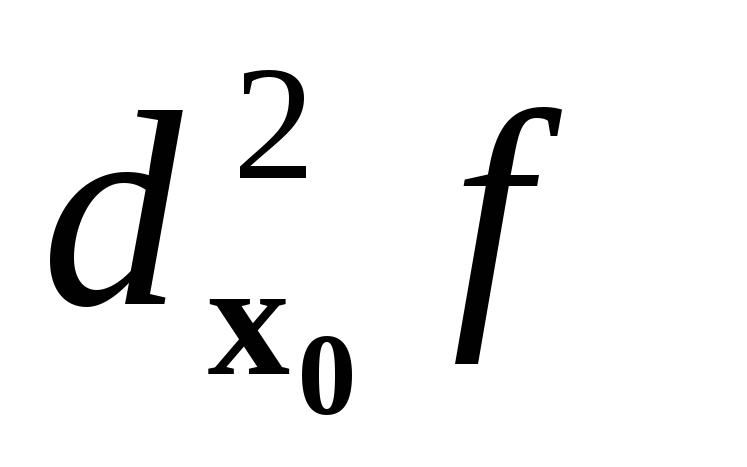 -
отрицательно
определенная квадратичная форма, то
х0
является
точкой строгого максимума функции f
;
-
отрицательно
определенная квадратичная форма, то
х0
является
точкой строгого максимума функции f
; -
если
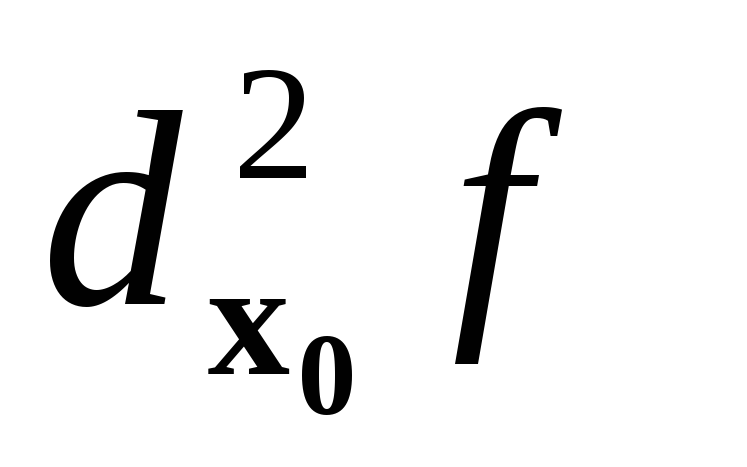 -
знакопеременная квадратичная форма,
то х0
не
яв- ляется
точкой экстремума функции f
.
-
знакопеременная квадратичная форма,
то х0
не
яв- ляется
точкой экстремума функции f
.
►
Выберем
ε
>0 такое,
чтобы f
была дважды
дифференцируема в ε
–окрестности
![]() (
ε).
По теореме Тейлора-Пеано (см. [3], стр.32,
при m=
2) при всяком
х,
принадлежащем
(
ε).
По теореме Тейлора-Пеано (см. [3], стр.32,
при m=
2) при всяком
х,
принадлежащем
![]() (
ε),
имеем :
(
ε),
имеем :
![]() (1)
(1)
Здесь
h=
x-
x0
,
![]() Заметим: f(x)
- f(x0)
= f(x0+h)
- f(x0)
=
Заметим: f(x)
- f(x0)
= f(x0+h)
- f(x0)
=
![]() .
Так как х0
–
стационарная
точка, то
df(h)≡0.
Из (1) получим:
.
Так как х0
–
стационарная
точка, то
df(h)≡0.
Из (1) получим:
![]()
![]()
![]()
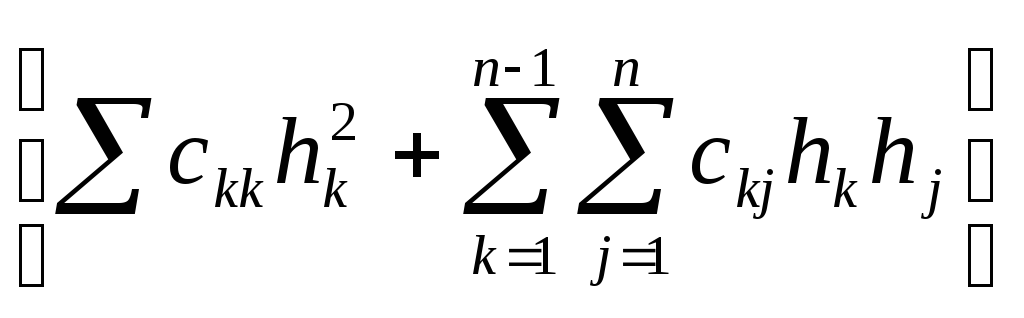 +
+
![]() ,
(2) где
,
(2) где
![]() ,
а h
= (h1,h2.
…,hn).
,
а h
= (h1,h2.
…,hn).
Пусть
h
![]()
![]() такое ,
что 0 <
такое ,
что 0 <
![]() .
Обозначим: u=
.
Обозначим: u=![]() .
Заметим: ||u||
= 1,
и если u
= (u1,u2,
… ,un),
то uk
=
.
Заметим: ||u||
= 1,
и если u
= (u1,u2,
… ,un),
то uk
=
![]() ,
k
= 1,2, … , n.
Из (2) следует:
,
k
= 1,2, … , n.
Из (2) следует:
![]() =
=![]()
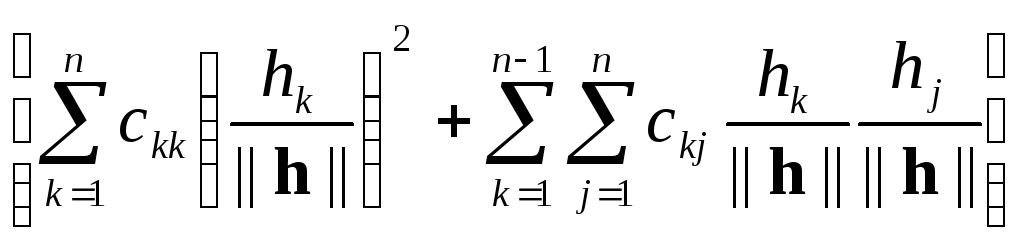 +
+
![]() = =
= = =
=
![]() = =
= =![]() =
=
![]() ,
(3)
где
,
(3)
где
![]() при h
→ 0.
при h
→ 0.
Обозначим
через S
единичную
сферу в пространстве
![]() -
совокуп-
ность тех элементов пространства
-
совокуп-
ность тех элементов пространства
![]() ,
норма
которых равна единице: S
=
,
норма
которых равна единице: S
=
![]() .
Квадратичная форма
.
Квадратичная форма
![]() -
непрерыв- ная функция.
По теореме
Вейерштрасса ([3 ], стр.15 )
-
непрерыв- ная функция.
По теореме
Вейерштрасса ([3 ], стр.15 )
![]() достигает
на ог- раниченном замкнутом множестве
S
своего
наименьшего и своего наиболь- шего
значений – обозначим их через m
и
M
соответственно.
Значит, на S
существуют точки h*
и h
достигает
на ог- раниченном замкнутом множестве
S
своего
наименьшего и своего наиболь- шего
значений – обозначим их через m
и
M
соответственно.
Значит, на S
существуют точки h*
и h![]() такие,
что
такие,
что
![]() ,
M
=
,
M
=
![]()
Так
как u
![]() S,
справедливы
неравенства m
≤
S,
справедливы
неравенства m
≤
![]() ≤
M,
и, следова- тельно (см. (3)
), при всяком
h
≤
M,
и, следова- тельно (см. (3)
), при всяком
h
![]()
![]() ,
0 <
,
0 <
![]() ,
имеем
:
,
имеем
:
||h||![]()
![]() ≤
≤
![]() ≤ ||h||
≤ ||h||![]()
![]() (4)
(4)
-
Пусть
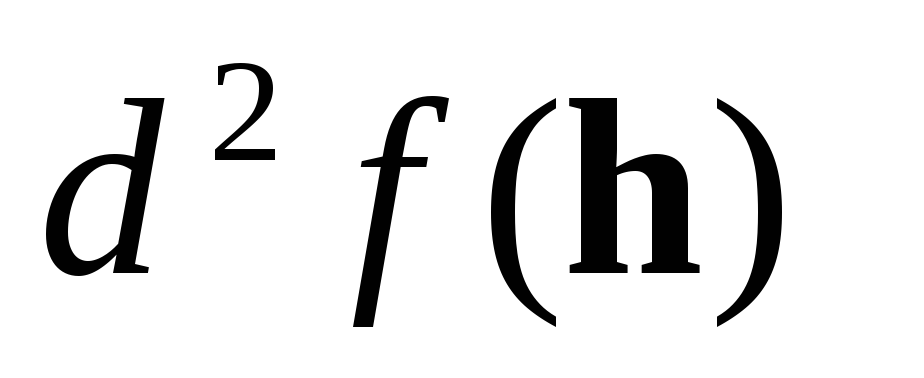 -
положительно определенная форма, т.е.
её значе- ние положительно на любом
элементе пространства
-
положительно определенная форма, т.е.
её значе- ние положительно на любом
элементе пространства
 ,отличном
от 0 .
,отличном
от 0 .
Заметим:
m
>0, ибо
m=![]() ,
а h*≠
0 (
ведь ||h*||
=1)
. Так как
,
а h*≠
0 (
ведь ||h*||
=1)
. Так как
![]() при h
→ 0, можно
подобрать δ
, 0 < δ
< ε,
так, что при всяком h
таком,что 0
< ||h||
< δ
будет выполнено
при h
→ 0, можно
подобрать δ
, 0 < δ
< ε,
так, что при всяком h
таком,что 0
< ||h||
< δ
будет выполнено
![]() m.
Отсюда и из
(4) следует: при всех h
m.
Отсюда и из
(4) следует: при всех h
![]() ,
0 < ||h||
< δ,
справедливо
,
0 < ||h||
< δ,
справедливо
![]() >
0.
Значит (см.
II)
х0
явля- ется
точкой строгого минимума функции f
.
>
0.
Значит (см.
II)
х0
явля- ется
точкой строгого минимума функции f
.
-
Пусть
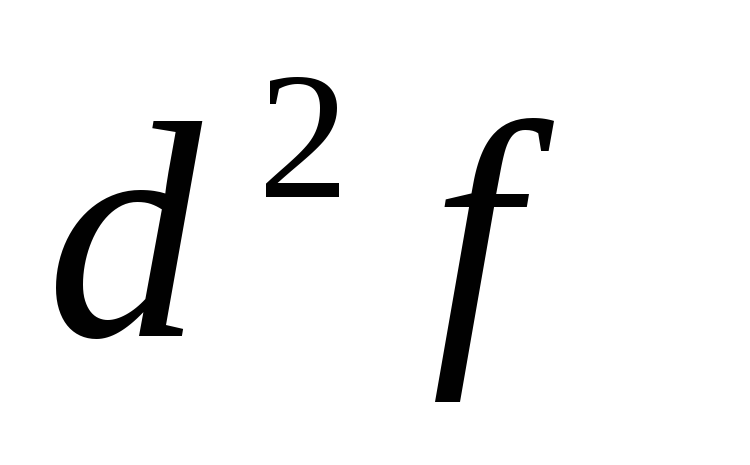 -
отрицательно определенная форма, т.е.
её значение отрицательно на любом
элементе пространства
-
отрицательно определенная форма, т.е.
её значение отрицательно на любом
элементе пространства
 ,отличном
от 0 .
,отличном
от 0 .
Заметим:
M
< 0, ибо M
![]() ,
а h
,
а h![]() ≠ 0.
Найдётся δ
, 0 < δ
< ε,
такое, что при всех h
≠ 0.
Найдётся δ
, 0 < δ
< ε,
такое, что при всех h
![]() ,
удовлетворяющих требованиям 0
< ||h||
< δ
справедливо
,
удовлетворяющих требованиям 0
< ||h||
< δ
справедливо
![]() |M|.
Из (4) следует, что при тех же h
справедливо
|M|.
Из (4) следует, что при тех же h
справедливо
![]() <
0. Зна- чит (см. II),
х0
является
точкой строгого максимума функции f
.
<
0. Зна- чит (см. II),
х0
является
точкой строгого максимума функции f
.
-
Пусть
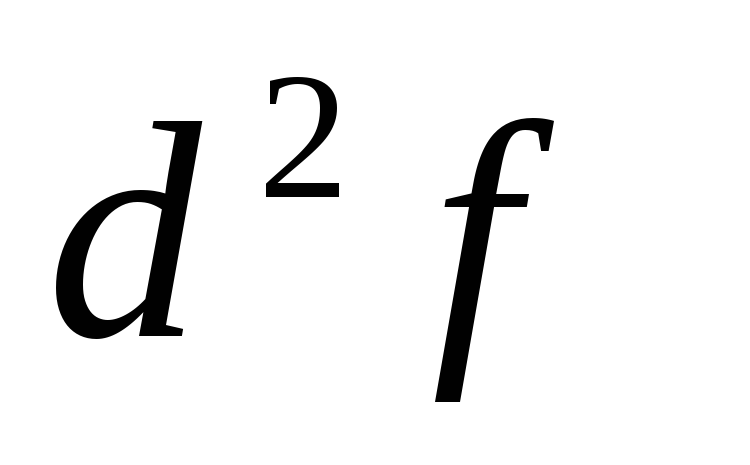 -
знакопеременная квадратичная форма и
пусть h′
= =
-
знакопеременная квадратичная форма и
пусть h′
= = и
h″
=
и
h″
=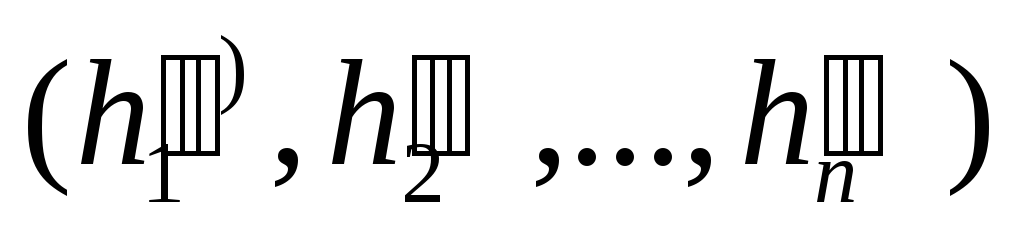 такие,
что
такие,
что
 (
h′)>0,
(
h′)>0,
 (
h″)<0.
(
h″)<0.
Положим
h = t h′, где
![]() R
. Заметим: h =
(h1,h2. …,hn), где
hk = t
R
. Заметим: h =
(h1,h2. …,hn), где
hk = t![]() ,
k = 1,2, … ,n. При всех
,
k = 1,2, … ,n. При всех
![]() R
R
![]() =
=![]()
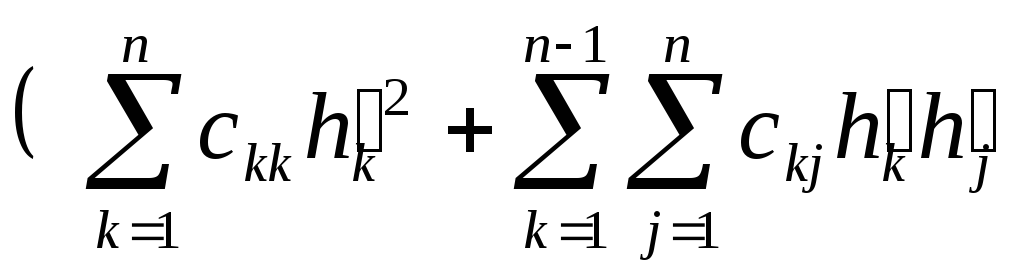
![]() =
=![]() .
Таким
образом, при
всех
.
Таким
образом, при
всех
![]()
![]() .
Кроме того, из (2)
следует:
.
Кроме того, из (2)
следует:
![]() =
=
![]()
![]()
![]() +
+![]()
=
![]()
![]() +
+![]()
![]() .
Так как
.
Так как
![]() при
при
![]() ,
существует
,
существует
![]() ,
такое, что при
,
такое, что при
![]() вы- полняется
вы- полняется
![]() <
<![]()
![]() .
Из
.
Из
![]() =
=
![]() теперь сле- дует: при
всех
теперь сле- дует: при
всех
![]() ,
,
![]() ,
справедливо
,
справедливо
![]() .
.
Положив
h = t
h″,
где
![]() R
, аналогично получим: при
всех
R
, аналогично получим: при
всех
![]() :
:
![]()
![]() < 0 .;
< 0 .;
![]() =
=
![]() .
Существует
.
Существует![]() ,
такое, что при
,
такое, что при
![]() выполняется
выполняется
![]() <
<![]() |
|![]() |
Из
|
Из
![]() =
=
![]() вытекает: при всех
вытекает: при всех
![]() ,
,
![]() справед-
ливо
справед-
ливо
![]() .
.
