
- •§ 1. Пространство и его подмножества
- •§ 2. Функция n переменных, ее предел и непрервность
- •§ 3. Частные производные и дифференциал функции n, n2,
- •Обозначают введенную этим определением частную производную символами fх′(m0) или fх′(x0,y0) , а также
- •§ 4. Неявные функции.
- •§ 5. Свободный экстремум функции нескольких переменных
- •Пусть , а - любое, удовлетворяющее условиям . Взяв , удовлетворяющее указанным условиям, выберем для этого число такое, что и обозначим: . Имеем: , причём ;
- •§ 6. Условный экстремум
- •6. 3. Метод Лагранжа
- •В силу инвариантности формы первого дифференциала имеем:
- •Литература
- •§ 1. Пространство и его подмножества
- •Пространство …………………………. 3
- •§ 2. Функция n переменных, её предел и непрерывность
- •§ 3. Частные производные и дифференциалы
- •§ 4. Неявные функции
- •§ 5. Свободный экстремум функции нескольких переменных
- •§ 6. Условный экстремум
Пусть , а - любое, удовлетворяющее условиям . Взяв , удовлетворяющее указанным условиям, выберем для этого число такое, что и обозначим: . Имеем: , причём ;
![]()
![]() ,
причём
,
причём
![]()
![]() .
Итак,
при всяком δ
,
.
Итак,
при всяком δ
,
![]()
![]() можно указать h1
и h2 такие,
что ||h1||
< δ,
||h2|| < δ,
а соответствующие приращения
можно указать h1
и h2 такие,
что ||h1||
< δ,
||h2|| < δ,
а соответствующие приращения
![]() и
и
![]() отличны
от нуля и имеют противоположные знаки;
значит (см. Ш) х0
не является
точкой экстремума функции f.
◄
отличны
от нуля и имеют противоположные знаки;
значит (см. Ш) х0
не является
точкой экстремума функции f.
◄
Запишем
матрицу квадратичной формы
![]() :
:
C =
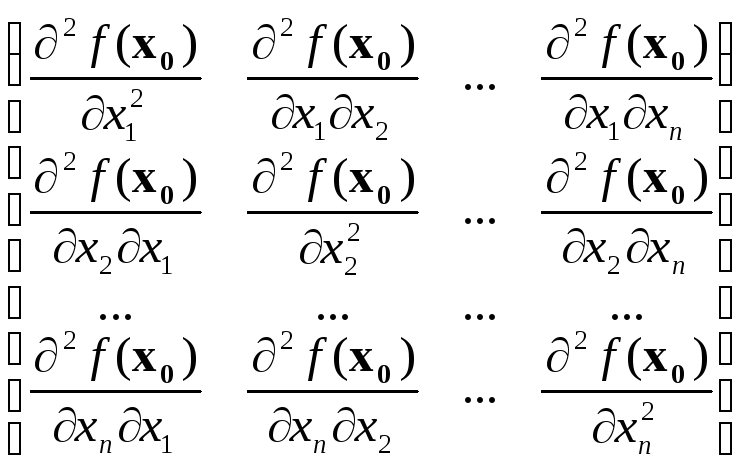
Пусть Δ1, Δ2, … ,Δn - последовательные угловые миноры этой матрицы:
Δ1=
![]() ,
Δ2
=
,
Δ2
=
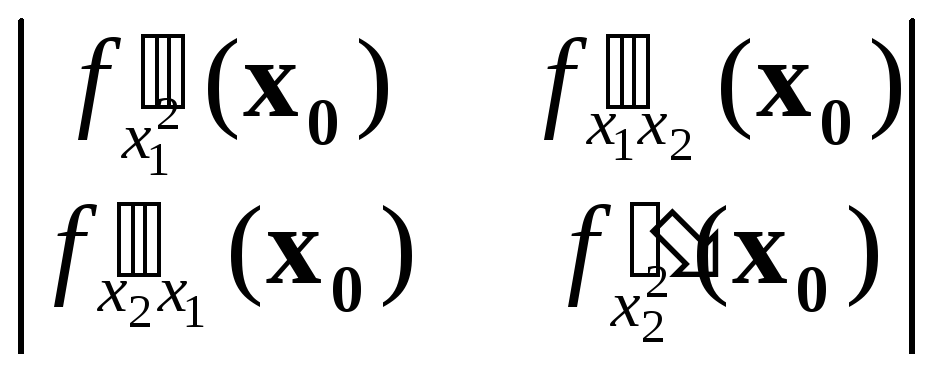 ,
… , Δn
=det
C.
,
… , Δn
=det
C.
Следствие. Пусть точка х0 и функция f удовлетворяют условиям тео- ремы 2. Тогда : 1) если Δk > 0, k =1,2,…,n, то х0 есть точка строгого миниму- ма функции f ; 2) если все угловые миноры отличны от нуля, а их знаки че- редуются, причём Δ1 < 0, то х0 есть точка строгого максимума функции f.
Справедливость этих утверждений непосредственно вытекает из теоре- мы 2 и критерия Сильвестра ([4], стр. 21).
Замечание.
Если угловые миноры матрицы С не
удовлетворяют требо- ваниям критерия
Сильвестра, форма
![]() либо квазизнакоопределенная, ли- бо
знакопеременная. В первом случае
стационарная точка х0
может оказать- ся точкой экстремума, но
может ею и не быть. Исследование
стационарной точки в этом случае
проводится с привлечением дифференциалов
более вы- соких порядков.
либо квазизнакоопределенная, ли- бо
знакопеременная. В первом случае
стационарная точка х0
может оказать- ся точкой экстремума, но
может ею и не быть. Исследование
стационарной точки в этом случае
проводится с привлечением дифференциалов
более вы- соких порядков.
Рассмотрим
отдельно случай функции f(x,y)
двух переменных. Запишем
![]() такой
функции:
такой
функции:
![]()
Запишем матрицу этой квадратичной формы от двух переменных h1 и h2 и её угловые миноры:
С
=
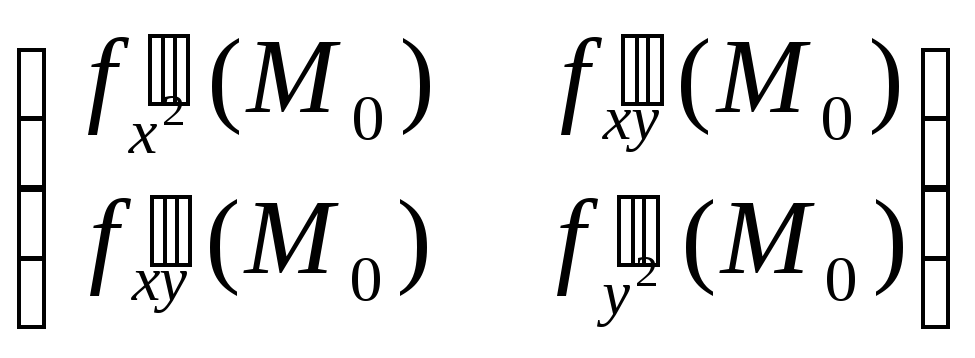 ,
,
Δ1
=
![]() ,
Δ2
=
,
Δ2
=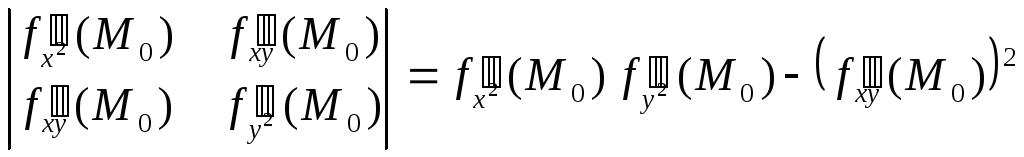 .
.
Теорема 3. Пусть функция f (х,у) дважды дифференцируема в окрест- ности точки М0(х0,у0), которая является стационарной точкой этой функции. Тогда:
-
если Δ2 =
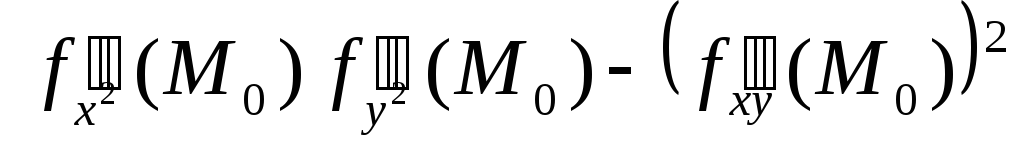 >
0, то М0
есть точка строгого экс- тремума функции
f, а
именно, строгого минимума в случае
>
0, то М0
есть точка строгого экс- тремума функции
f, а
именно, строгого минимума в случае
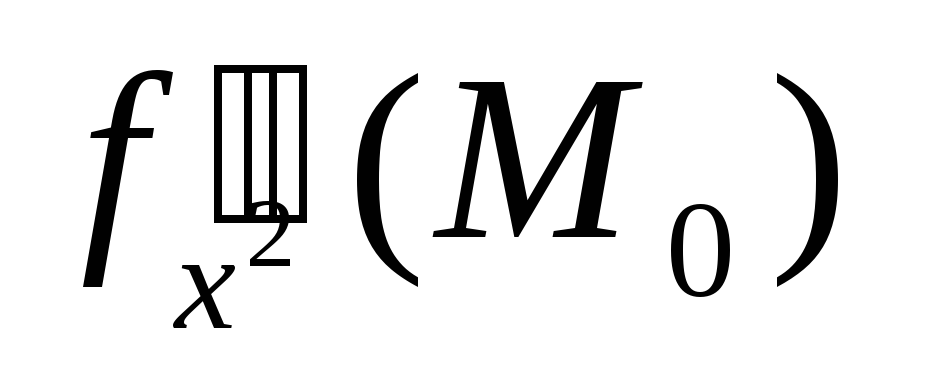 >
0 и строгого
максимума в случае
>
0 и строгого
максимума в случае
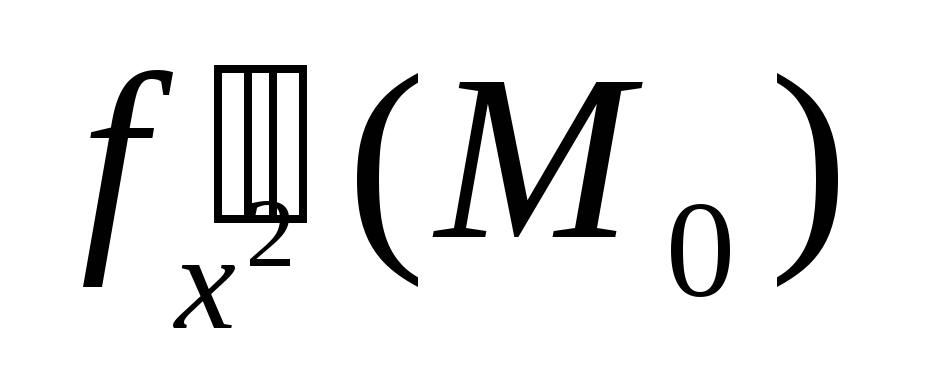 <
0;
<
0; -
если Δ2 =
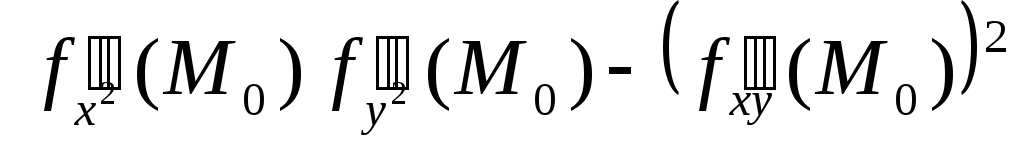 <
0, то М0
не
является точкой экстремума функции f.
<
0, то М0
не
является точкой экстремума функции f.
► Утверждения 1) вытекают непосредственно из следствия теоремы 2. Докажем утверждение 2).
Пусть
![]() <
0. Может
представиться один из сле- дующих трёх
случаев:
<
0. Может
представиться один из сле- дующих трёх
случаев:
*)
![]() ≠0,
**)
≠0,
**)
![]() =0,
но
=0,
но
![]() ≠0,
***)
≠0,
***)![]() =
=![]() =0.
=0.
Покажем
что в каждом из этих случаев
![]() является
знакопеременной формой
является
знакопеременной формой
*) Нетрудно проверить справедливость при любых h1 и h2 равенства
![]() =
=
![]()
Положив
здесь сначала
![]() а затем
а затем
![]()
![]()
![]() получим:
получим:
![]() ,
,
![]() {
{![]() }.
По условию выражение
в фигурных скобках отрицательно; значит,
в точках
}.
По условию выражение
в фигурных скобках отрицательно; значит,
в точках
![]() и
и
![]() форма
форма
![]() принимает значения противополож- ных
знаков, т.е. это знакопеременная форма
.
принимает значения противополож- ных
знаков, т.е. это знакопеременная форма
.
**)
Из![]() =0
и
=0
и
![]() <
0 следует
<
0 следует
![]() .
Положив в
.
Положив в
![]() =
=![]() сначала
сначала
![]() а затем
а затем
![]()
![]()
![]() получим:
получим:
![]() ,
,
![]()
![]()
![]() .
Отсюда
ясно, что
.
Отсюда
ясно, что
![]() -
знакопеременная форма.
-
знакопеременная форма.
***)
Имеем
![]() ,
причем
,
причем
![]() .
Легко видеть, что это знакопеременная
форма.
.
Легко видеть, что это знакопеременная
форма.
Итак,
если![]() <
0, то
<
0, то
![]() представляет собой знакопеременную
форму. В силу утверждения 3) теоремы 2 М0
не
является точкой экстремума функции f.
◄
представляет собой знакопеременную
форму. В силу утверждения 3) теоремы 2 М0
не
является точкой экстремума функции f.
◄
Пример
3. Для
каждой из
функций
f1(x,y)
=
![]() ,
,
![]()
![]() и
и
![]() точка О(0,0)
является стационарной, причем для f1
и f2
в этой точке Δ2
> 0 , а для
f4
в этой
точке Δ2
< 0.
Значит, точка О(0,0)
является точкой экстремума для f1
и f2
, и не
является точкой экстре- мума для f4
. Для
функции f1
имеем:
точка О(0,0)
является стационарной, причем для f1
и f2
в этой точке Δ2
> 0 , а для
f4
в этой
точке Δ2
< 0.
Значит, точка О(0,0)
является точкой экстремума для f1
и f2
, и не
является точкой экстре- мума для f4
. Для
функции f1
имеем:![]() ;
следовательно, О(0,0)
есть точка строгого минимума этой
функции f1.
Для функции f2
:
;
следовательно, О(0,0)
есть точка строгого минимума этой
функции f1.
Для функции f2
:![]() ;
значит, f2
имеет в
О(0,0)
строгий максимум (рис.1).
;
значит, f2
имеет в
О(0,0)
строгий максимум (рис.1).
Замечание
7. В случае
Δ2
=![]() =0
точка М0
может
оказаться точкой экстремума, но может
и не быть ею.
=0
точка М0
может
оказаться точкой экстремума, но может
и не быть ею.
Пример
4. Пусть
![]() .
Для каждой из этих функ- ций точка О(0,0)
является стационарной, причем Δ2
= 0. Ясно, что наимень- шее значение f5
равно нулю, и оно достигается во всех
точках, лежащих на прямой х+у=0
; таким образом, для этой функции О(0,0)
есть точка миниму- ма (нестрогого). Что
касается f6
, то f6(0,0)
= 0, причем в любой окрестности начала
координат имеются как точки, в которых
значения этой функции по- ложительны,
так и точки, в которых её значения
отрицательны; следователь- но, О(0,0)
не является точкой экстремума функции
f6
.
.
Для каждой из этих функ- ций точка О(0,0)
является стационарной, причем Δ2
= 0. Ясно, что наимень- шее значение f5
равно нулю, и оно достигается во всех
точках, лежащих на прямой х+у=0
; таким образом, для этой функции О(0,0)
есть точка миниму- ма (нестрогого). Что
касается f6
, то f6(0,0)
= 0, причем в любой окрестности начала
координат имеются как точки, в которых
значения этой функции по- ложительны,
так и точки, в которых её значения
отрицательны; следователь- но, О(0,0)
не является точкой экстремума функции
f6
.
