
- •§ 1. Пространство и его подмножества
- •§ 2. Функция n переменных, ее предел и непрервность
- •§ 3. Частные производные и дифференциал функции n, n2,
- •Обозначают введенную этим определением частную производную символами fх′(m0) или fх′(x0,y0) , а также
- •§ 4. Неявные функции.
- •§ 5. Свободный экстремум функции нескольких переменных
- •Пусть , а - любое, удовлетворяющее условиям . Взяв , удовлетворяющее указанным условиям, выберем для этого число такое, что и обозначим: . Имеем: , причём ;
- •§ 6. Условный экстремум
- •6. 3. Метод Лагранжа
- •В силу инвариантности формы первого дифференциала имеем:
- •Литература
- •§ 1. Пространство и его подмножества
- •Пространство …………………………. 3
- •§ 2. Функция n переменных, её предел и непрерывность
- •§ 3. Частные производные и дифференциалы
- •§ 4. Неявные функции
- •§ 5. Свободный экстремум функции нескольких переменных
- •§ 6. Условный экстремум
§ 4. Неявные функции.
Неявными называют функции, задание которых осуществляется пос – редством уравнения или системы уравнений.
-
Неявная функция, заданная уравнением F(x,y)= 0.
Приведем пример функции, заданной уравнением.
Пример.
Рассмотрим
уравнение F(x,y)
= 0, где
F(x,y)
=![]() .
Функция F(x,y)
определена при
любых х и
у. Зафиксируем
некоторое х0
и обозначим: g(y)=
F(x0,y)
=
.
Функция F(x,y)
определена при
любых х и
у. Зафиксируем
некоторое х0
и обозначим: g(y)=
F(x0,y)
=![]() .
Функция g(y)
непрерывна на всей числовой оси,
.
Функция g(y)
непрерывна на всей числовой оси,
![]() .
Кроме того, так как при всех у
.
Кроме того, так как при всех у
![]() ,
g(y)
убывает на
,
g(y)
убывает на
![]() от
от
![]() до
до
![]() .
Следова- тельно, существует и при том
только одно у0
такое, что
g(y0)
=
.
Следова- тельно, существует и при том
только одно у0
такое, что
g(y0)
=
![]() ,
т.е. F(x0,y0)
= 0. Так как
число х0
может
быть выбрано любым, то установлен
следующий факт: для всякого
,
т.е. F(x0,y0)
= 0. Так как
число х0
может
быть выбрано любым, то установлен
следующий факт: для всякого
![]()
![]() существует единственное число у
такое, что F(x,y)
= 0. Зададим на
существует единственное число у
такое, что F(x,y)
= 0. Зададим на
![]() функцию
функцию
![]() ,
сформулировав следующее правило
,
сформулировав следующее правило![]() :
каждому
:
каждому
![]()
![]() поставим в соответствие число у
такое, что
F(x,y)=
0. Чтобы для заданного
х найти
соответствующее ему значение функ- ции
у =
поставим в соответствие число у
такое, что
F(x,y)=
0. Чтобы для заданного
х найти
соответствующее ему значение функ- ции
у =![]() ,
нужно из равенства
,
нужно из равенства
![]()
![]() =0 найти у,
выразив его
через х.
Очевидно,
однако, что сделать это не удастся. Таким
образом, урав- нение
=0 найти у,
выразив его
через х.
Очевидно,
однако, что сделать это не удастся. Таким
образом, урав- нение
![]() =0
определяет на всей
числовой оси функцию
=0
определяет на всей
числовой оси функцию
![]() ,
причём получить
её явное задание в виде формулы у
=
,
причём получить
её явное задание в виде формулы у
=![]() не удаётся. Отметим следующее свойство
не удаётся. Отметим следующее свойство
![]() :
при всяком
:
при всяком
![]()
![]() F(x,
F(x,
![]() )
= 0, т.е.
F(x,
)
= 0, т.е.
F(x,
![]() )
≡ 0 на
)
≡ 0 на
![]() .
.
Пусть
F(x,y)-
функция,
определеная
на некотором множестве D![]() ,
а f(х)
- функция, определеная на некотором
промежутке Х.
Если
при каждом х
,
а f(х)
- функция, определеная на некотором
промежутке Х.
Если
при каждом х![]() Х
точка Р(х,
f(х)) принадлежит
D,
а F(x,
f(х)) ≡ 0 на Х
, будем
говорить, что
функция f(х)
удовлетворяет
на промежутке Х
уравнению
F(x,y
)=
0;
функцию f(х)
будем называть
при этом
решением
уравнения F(x,y)
= 0 на промежутке
Х.
Будем также говорить, что уравнение
F(x,y) = 0
неявно задает функцию f(х)
на промежутке
Х
.
Х
точка Р(х,
f(х)) принадлежит
D,
а F(x,
f(х)) ≡ 0 на Х
, будем
говорить, что
функция f(х)
удовлетворяет
на промежутке Х
уравнению
F(x,y
)=
0;
функцию f(х)
будем называть
при этом
решением
уравнения F(x,y)
= 0 на промежутке
Х.
Будем также говорить, что уравнение
F(x,y) = 0
неявно задает функцию f(х)
на промежутке
Х
.
Пусть
имеем некоторое уравнение F(x,y)
= 0. Такое
уравнение может иметь единственное
решение f(х)
( см. пример
выше). Уравнение может иметь несколько
решений; например, две функции
![]() и
и
![]()
![]() удовлетворяют на
удовлетворяют на
![]() уравнению
уравнению
![]() .
Уравнение может не иметь решений;
примером такого уравнения является
.
Уравнение может не иметь решений;
примером такого уравнения является
![]() .
Ответ на вопрос о существовании и
количестве решений заданного уравнения
F(x,y) = 0
будет получен, если разрешить уравнение
относительно у,
выразив его
через х.
Однако,
сделать это не всегда возможно
( см. пример
выше). В таких случаях полезна следующая
теорема.
.
Ответ на вопрос о существовании и
количестве решений заданного уравнения
F(x,y) = 0
будет получен, если разрешить уравнение
относительно у,
выразив его
через х.
Однако,
сделать это не всегда возможно
( см. пример
выше). В таких случаях полезна следующая
теорема.
Теорема
1 (О
существовании решения уравнения
F(x,y) = 0
) Пусть
функция F(x,y)
непрерывно дифференцируема в окрестности
точки Р0(х0,у0),
и пусть F(x0,y0)=0,
а
![]() 0.
Тогда существуют положительные
0.
Тогда существуют положительные
![]() и
и![]() ,
а также единственная функция f(х)
такая, что
,
а также единственная функция f(х)
такая, что
-
f(х) является решением уравнения F(x,y) = 0 на интервале (
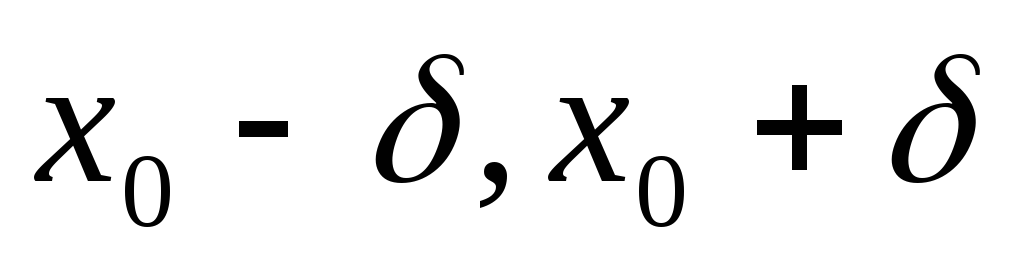 );
); -
для всякого
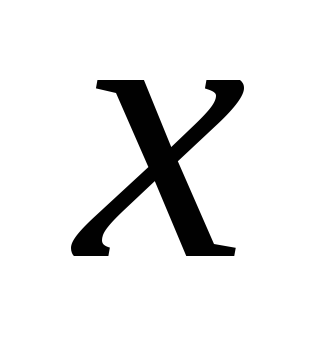
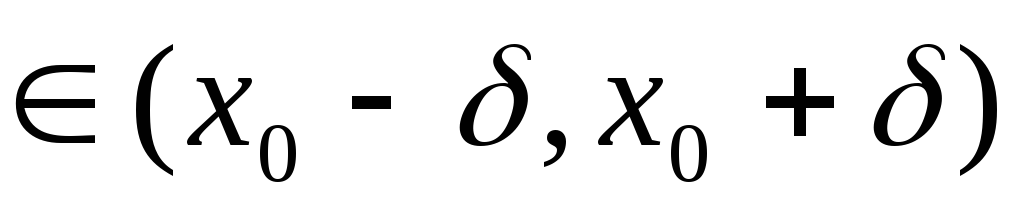 справедливы неравенства
справедливы неравенства
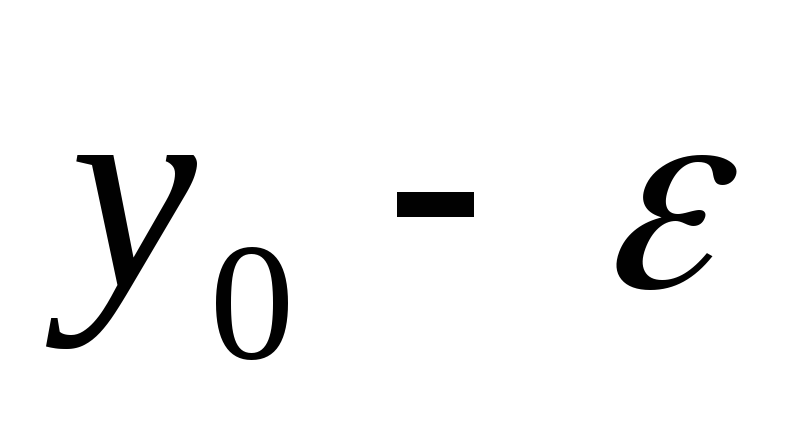 <
< <
<
<
<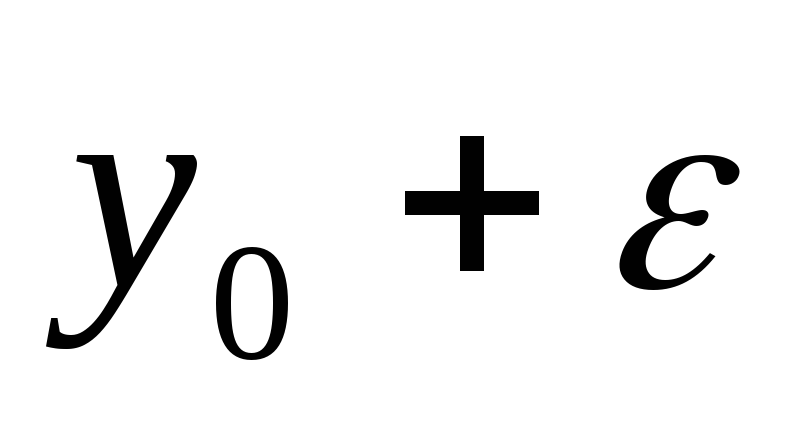 ,
причём
,
причём
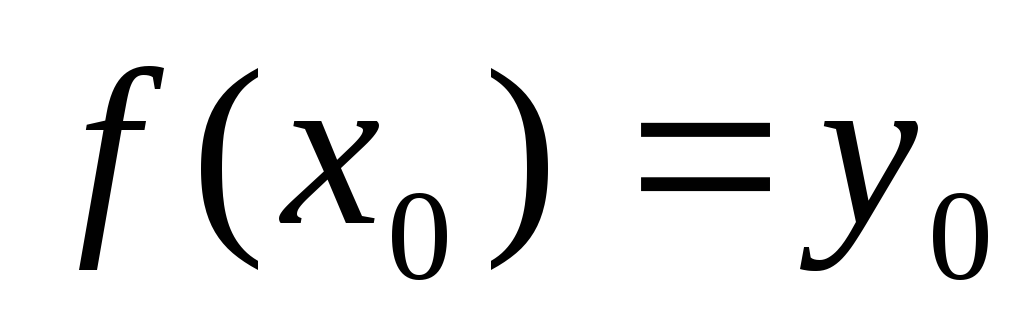 ;
; -
функция f(х) непрерывно дифференцируема на (
 ),
при- чём для
всякого
),
при- чём для
всякого
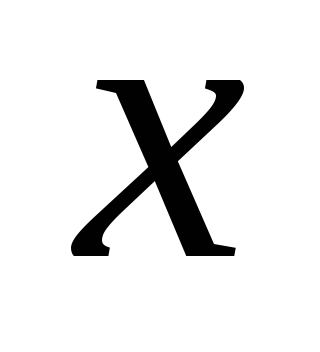
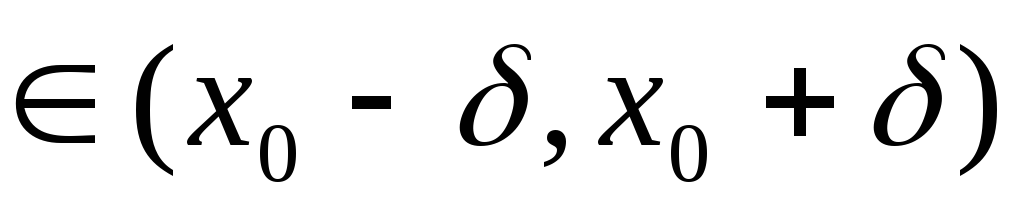

 .
.
Доказательство
этой теоремы имеется в [1]. Остановимся
на ее гео -метрическом смысле. Уравнение
F(x,y) = 0
задает на плоскости некоторую кривую
Г ;
так как
F(x0,y0)=0,
она проходит через точку Р0(х0,у0).
Та часть этой кривой, которая попадает
внутрь прямоугольника, ограниченного
пря- мыми
![]()
![]()
![]()
![]() представляет собой график γ функции
представляет собой график γ функции
![]() на интервале
на интервале
![]() .
.
4.2.
Неявная
функция, заданная уравнением F (![]() ,
u) = 0
,
u) = 0
Пусть
функция F (![]() ,
u) определена
на некотором множестве D,
лежащем в
пространстве
,
u) определена
на некотором множестве D,
лежащем в
пространстве![]() ,
а функция
f(x)
= f (
,
а функция
f(x)
= f (![]() )
определена на множестве Х
)
определена на множестве Х![]() .
Будем говорить, что функция f(x)
удовлетворяет
уравне- нию F(x,
u) = 0 на
множестве Х
, если при каждом x
.
Будем говорить, что функция f(x)
удовлетворяет
уравне- нию F(x,
u) = 0 на
множестве Х
, если при каждом x![]() Х
точка (x,
f(x))
= =(x1,x2,…,xn,
f (x1,x2,…
,xn))
принадлежит
D,
а F(x,
f(x))
≡ 0 на Х;
при
этом функцию f(x)
будем называть решением уравнения F(x,
u)
= 0 на множестве
Х. Будем
также говорить, что уравнение F(x,
u) = 0 неявно
задает функцию f(х)
на множестве
Х.
Х
точка (x,
f(x))
= =(x1,x2,…,xn,
f (x1,x2,…
,xn))
принадлежит
D,
а F(x,
f(x))
≡ 0 на Х;
при
этом функцию f(x)
будем называть решением уравнения F(x,
u)
= 0 на множестве
Х. Будем
также говорить, что уравнение F(x,
u) = 0 неявно
задает функцию f(х)
на множестве
Х.
Уравнение
F(x,
u) = 0 может
иметь единственное решение f(х),
может иметь несколько решений или вовсе
не иметь решений. Так, функция
![]()
![]() является
единственным решением уравнения
является
единственным решением уравнения
![]()
![]() ,
каждая из функций
,
каждая из функций
![]() удовлетворяет уравнению
удовлетворяет уравнению
![]() ,
а уравнение
,
а уравнение
![]() решений не имеет.
решений не имеет.
Ответ на вопрос о существовании и количестве решений заданного уравнения F(x, u) = 0 будет получен, если разрешить уравнение относитель- но u, выразив его через х= (x1,x2,…,xn). Однако, сделать это не всегда возмож- но. В таких случаях полезна следующая теорема.
Теорема
2. (О
существовании решения уравнения
F(x,
u)
= 0
) Пусть
функция F(x1,x2,…,xn,
u)=F(x,
u)
непрерывно дифференцируема в окрестности
точки Р0(х0,
u0),где
х0
= (![]() )
и пусть
)
и пусть
![]() =0,
а
=0,
а
![]() 0.
Тогда существуют положительные
0.
Тогда существуют положительные
![]() и
и
![]() ,
а также единственная функция f(х)
такая, что
,
а также единственная функция f(х)
такая, что
-
f(х) является решением уравнения F(x, u) = 0 в
 -
окрестности
-
окрестности
 точки х0
;
точки х0
; -
для всякого х
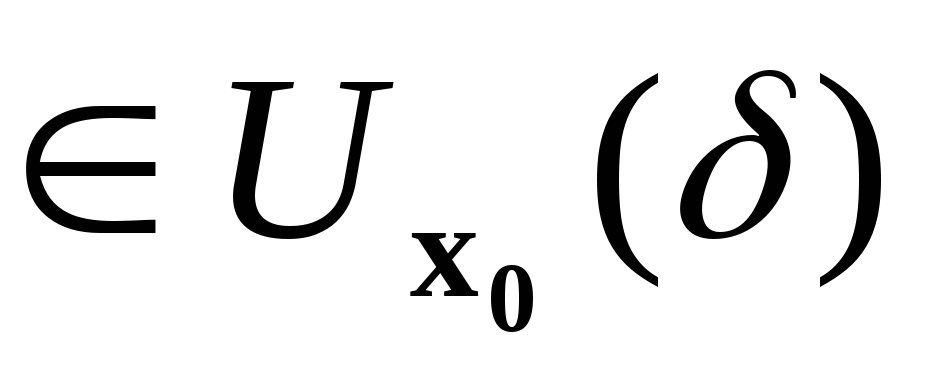 выполняется
выполняется
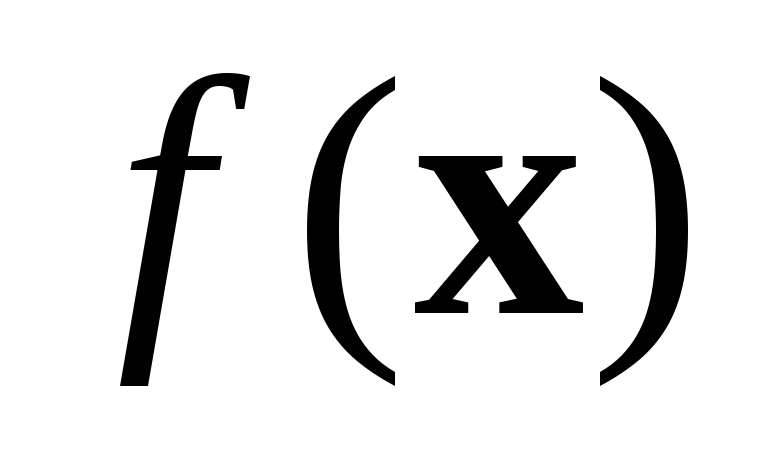
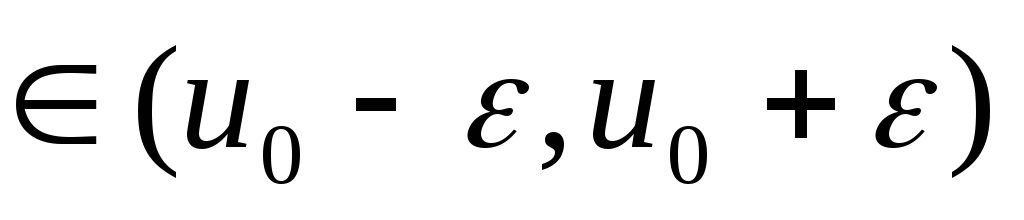 ,
причём
,
причём
 .
. -
Функция f(х) непрерывно дифференцируема в
 ,
и для всякого
х=
(x1,x2,
… ,xn)
,
и для всякого
х=
(x1,x2,
… ,xn)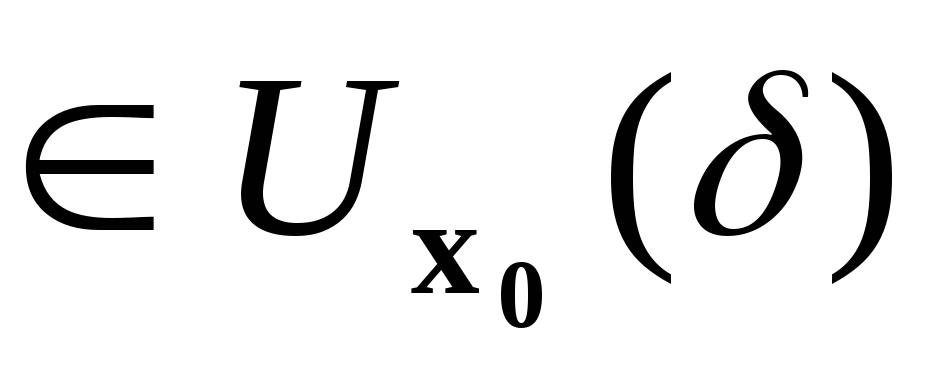 справедливы равенства
справедливы равенства
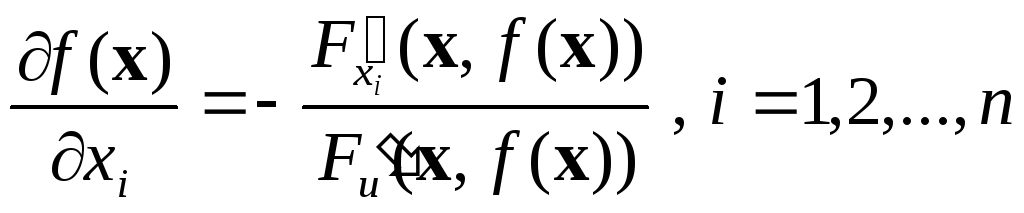 .
.
Геометрическая интерпретация этой теоремы возможна при n =2. Приведём сначала формулировку теоремы в этом случае.
Теорема
2'. Пусть
функция
![]() непрерывно
дифференцируема в
окрестности
точки Р0(х0,y0,
z0),
и пусть
непрерывно
дифференцируема в
окрестности
точки Р0(х0,y0,
z0),
и пусть
![]() =
0, а
=
0, а
![]()
![]() 0.
Тог- да существуют положительные
0.
Тог- да существуют положительные
![]() и
и
![]() ,
а также единственная функция f(х,y)
такая, что
,
а также единственная функция f(х,y)
такая, что
1)
f(х,y)
является решением уравнения
![]() =
0
в
=
0
в
![]() -
окрестности
-
окрестности
![]() точки Q0(х0,y0)
, т.е. в круге радиуса
точки Q0(х0,y0)
, т.е. в круге радиуса
![]() с центром Q0(х0,y0)
справед –ливо
с центром Q0(х0,y0)
справед –ливо
![]() 0
;
0
;
2)
для всякой
точки Q(х,у)
этого круга
![]() < f(х,y)
<
< f(х,y)
<
![]() ,
причём
,
причём
![]() .
.
3)
Функция f(х,y)
непрерывно
дифференцируема в
![]() ,
и для всякой
точки Q(х,у)
,
и для всякой
точки Q(х,у)![]() справедливы равенства
справедливы равенства
![]()
![]() .
.
Уравнение
![]() =
0 есть
уравнение некоторого геометрического
места точек Σ;
так как
=
0 есть
уравнение некоторого геометрического
места точек Σ;
так как
![]() =
0, точка
Р0(х0,y0,
z0)
принадлежит Σ.
Из утверждений 1) и 2) теоремы следует,
что та часть Σ
, которая содержится в прямом круговом
цилиндре
=
0, точка
Р0(х0,y0,
z0)
принадлежит Σ.
Из утверждений 1) и 2) теоремы следует,
что та часть Σ
, которая содержится в прямом круговом
цилиндре
С=
![]() ,
представляет собой
поверхность, а именно, график функции
,
представляет собой
поверхность, а именно, график функции
![]() на
круге
на
круге
![]() .
.
4.3. Неявные функции, заданные системой уравнений
Пусть
m
и n
– натуральные числа, и пусть m
функций Fk(u1,u2,…,
un,
un+1,
un+2,...,
un+m)
, k = 1,2,…, m
определены на некотором множестве D![]() .
.
Пусть
функции f j
(u1,
u2,
…, un)
, j = 1,2,… …,m,
определены на множе- стве Х
![]() .
Будем говорить, что функции f
j (u1,
u2,…,
un)
, j = 1,2,… …,
m,
удовлетворяют на множестве Х
системе m
уравнений
.
Будем говорить, что функции f
j (u1,
u2,…,
un)
, j = 1,2,… …,
m,
удовлетворяют на множестве Х
системе m
уравнений
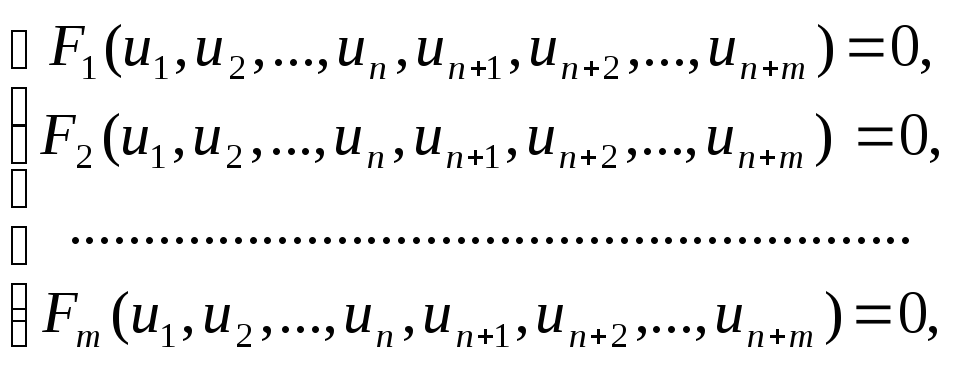
![]() (1)
если для всякой точки (u1,
u2,…,
un,)
(1)
если для всякой точки (u1,
u2,…,
un,)![]() точка
пространства
точка
пространства
![]()
(u1, u2,…, un, f1 (u1, u2,…, un), f2 (u1, u2,…, un),..., fm (u1, u2,…, un)) принадлежит множеству D , и при всех k = 1,2,…, m
Fk
(u1,u2,…,
un,
f1
(u1,
u2,…,
un),
f2
(u1,
u2,…,
un),...,
fm
(u1,
u2,…,
un))
≡ 0
на Х . (2)
Таким образом, после подстановки
![]() f j
(u1,
u2,…,
un)
, j = 1,2,… …,
m в
уравнения системы (1) левая часть каждого
уравнения тождественно равна нулю на
множестве Х.
Набор функций
f j
(u1,
u2,…,
un)
, j = 1,2,… …,
m в
уравнения системы (1) левая часть каждого
уравнения тождественно равна нулю на
множестве Х.
Набор функций
![]() ,
удовлетворяющий на множестве Х
системе (1),
будем называть решением системы (1) на
множест- ве Х.
Будем также
говорить, что функции f
j (u1,
u2,…,
un)
, j = 1,2,… …,
m
не- явно заданы на множестве Х
системой
(1).
,
удовлетворяющий на множестве Х
системе (1),
будем называть решением системы (1) на
множест- ве Х.
Будем также
говорить, что функции f
j (u1,
u2,…,
un)
, j = 1,2,… …,
m
не- явно заданы на множестве Х
системой
(1).
Пример. Рассмотрим систему
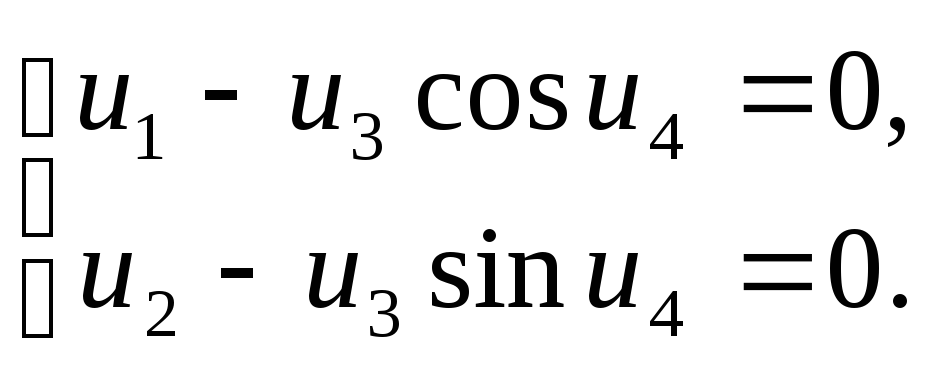 Здесь
Здесь
![]() ,
,
![]() .
Эти функции оп- ределены при любых
значениях переменных
.
Эти функции оп- ределены при любых
значениях переменных
![]() ;
следовательно,
;
следовательно,
![]()
![]() .
Уравнений два, значит, m=2,
а тогда и n=2.
Таким образом, решение системы (если
оно существует) представляет собой пару
функций двух пере- менных. Укажем одно
из решений этой системы. Подставив в
систему
.
Уравнений два, значит, m=2,
а тогда и n=2.
Таким образом, решение системы (если
оно существует) представляет собой пару
функций двух пере- менных. Укажем одно
из решений этой системы. Подставив в
систему
![]()
![]()
![]() ,
нетрудно убедиться, что пара
,
нетрудно убедиться, что пара
![]() является
решением системы (1) на множестве
является
решением системы (1) на множестве
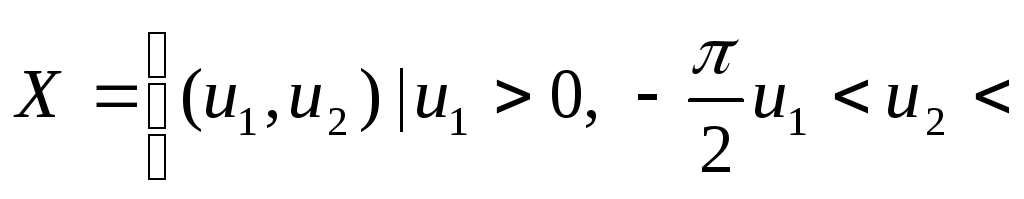
![]() .
.
Приведём формулировку теоремы о достаточных условиях существова- ния решения системы (1). Введём ряд обозначений:
х
= (х1,
х2,…,хn,)
, где
![]() ;
;
y=
(y1,
y2,…,ym,)
, где
![]() ;
;
u
= (u1,u2,…,
un,
un+1,
un+2,…,
un+m
)
=
(![]() )
= (х,у);
)
= (х,у);
Fk
(u1,u2,…,
un,
un+1,
un+2,…,
un+m
)
= Fk
(![]() )
= Fk
(х,у).
)
= Fk
(х,у).
В этих обозначениях система (1) запишется в компактной форме:
Fk
(х,у)
= 0,
![]() .
.
Пусть
u0
= (![]() )
– некоторая точка пространст- ва
)
– некоторая точка пространст- ва
![]() ,
а функции
Fk
(
,
а функции
Fk
(![]() ),
),![]() ,
дифференцируемы в окрестности этой
точки. Квадратную матрицу
,
дифференцируемы в окрестности этой
точки. Квадратную матрицу
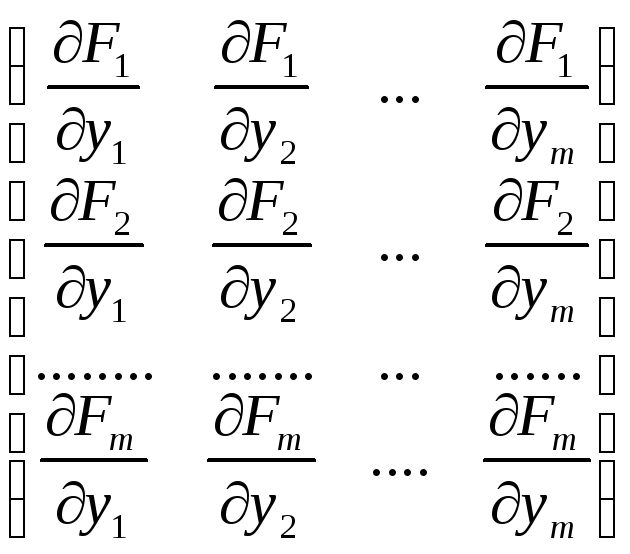 называют
матрицуей Якоби системы функций
называют
матрицуей Якоби системы функций
![]() по переменным
по переменным
![]() ,
а её определитель
называют якобианом этой систе- мы и
обозначают символом
,
а её определитель
называют якобианом этой систе- мы и
обозначают символом
![]() .
Якобиан системы
.
Якобиан системы
![]() явля- ется функцией переменных
явля- ется функцией переменных
![]() или точки u
= (
или точки u
= (![]()
![]() );
она определена в в окрестности
);
она определена в в окрестности
![]() точки
u0
. Значение
этой функции в точке u0
обозначим
через
точки
u0
. Значение
этой функции в точке u0
обозначим
через
![]()
Теорема
3 (О
существовании решения системы уравнений)
Пусть функции Fk
(х,у)
= 0,
![]() непрерывно дифференцируемы в окрестно-
сти
непрерывно дифференцируемы в окрестно-
сти
![]() точки u0
= (
точки u0
= (![]() )
, причем
)
, причем
*)
Fk(u0)
= 0,
![]() , и **)
, и **)
 0.
Тогда
существуют положительные
0.
Тогда
существуют положительные
![]() и
и
![]() и единственный набор функций
f j
(х1,х2,…,
хn)
, j = 1,2,… …,
m
такой, что
и единственный набор функций
f j
(х1,х2,…,
хn)
, j = 1,2,… …,
m
такой, что
1)
набор f j
(х1,х2,…,
хn)
, j = 1,2,… …,
m
является решением системы (1) в
![]() -
окрестности
-
окрестности
![]() точки х0
= (
точки х0
= (![]() );
);
2)
при любом х
= (![]() ),
принадлежащем
),
принадлежащем
![]() ,
справедливы неравенства
,
справедливы неравенства
![]() -
-![]() < f j
(x)
<
< f j
(x)
<![]() +
+![]() ,
j = 1,2,…
…, m,
причём f
j (x0)
=
,
j = 1,2,…
…, m,
причём f
j (x0)
=
![]() ,
j = 1,2,…
…, m;
,
j = 1,2,…
…, m;
3)
функции f j
(х1,х2,…,
хn)
, j = 1,2,… …,
m
непрерывно дифференци- руемы в
![]() .
.
Доказательство можно найти в руководствах по математическому анализу.
