18. Численное интегрирование методом неопределенных коэффициентов.

В рамках этого метода, производная в точке ищется в виде линейных комбинаций некоторых функций:

– неизвестное

В качестве функции берутся многочлены , точки – узлы интерполяции.

После подстановки этой функции получим:

Производная в точке :

При : .

Приравнивая значение производной при различных степенях получим систему уравнений:

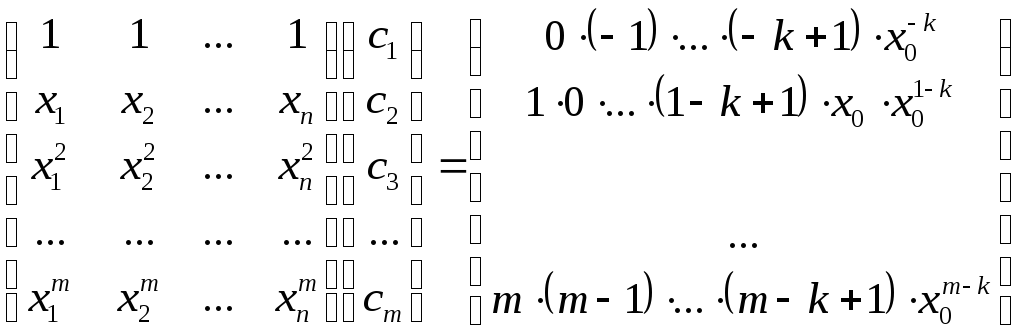
Решения возможны, если .

При определитель матрицы этой системы является определителем Вандермонда, и он отличен он нуля при различных значениях узлов.

Матрица определяется узлами интерполяции, а правая часть представляет собой вектор степеней в узлах, в которых мы оцениваем производную.

Таким образом, всегда можно построить формулу численного дифференцирования с n узлами точную для многочлена степени .

Частные случаи

Шаг дискретизации примем постоянным: .

Формулы численного дифференцирования точные для многочленов второго порядка. Число узлов интерполяции для многочлена второго порядка равно трем.

Примем эти узлы равными: .

Схема интерполяции:

Оценку интерполяции производим в точке, совпадающей с началом координат:

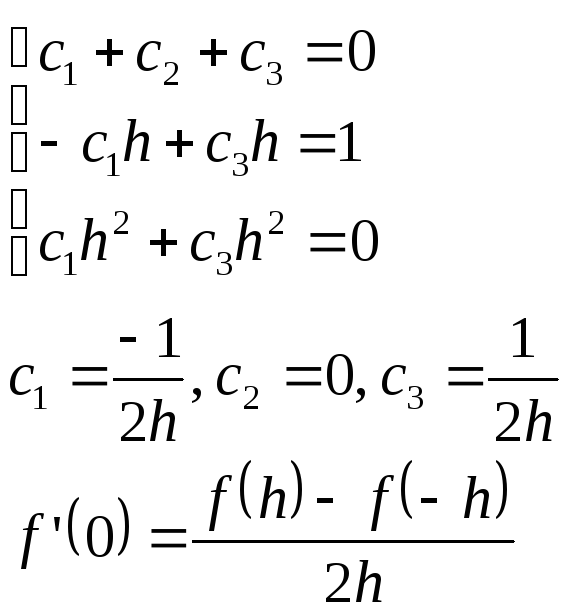
Рассмотрим равноотстоящую систему узлов:

Формулы вычисления второй производной, точной для многочлена второго порядка:

Получим систему уравнений, используя формулу для второй производной:

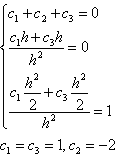
Получим формулу оценки производной в начале координат:

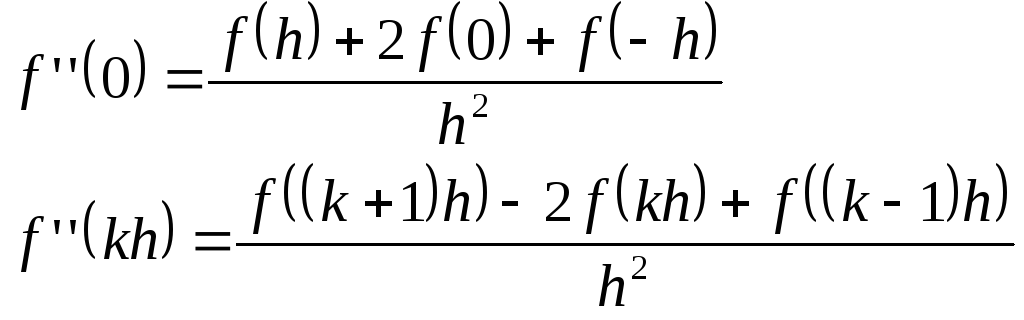
На практике часто используется несимметричная формула для производных:

I. 1)

2)

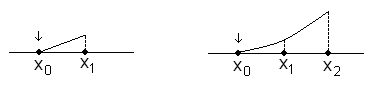
II. 1)

2)

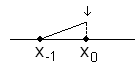
Оценка производной берется в самой точке и в предшествующих точках:

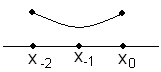
Существуют также формы для оценивания производных, расположенных между узлами интерполяции.

Несимметричные формулы для производных используются при численном решении дифференциальных уравнений.

Для этого все производные в дифференциальном уравнении выражаются через значение функции в соответствующих узлах интерполяции.

19. Квадратурные формулы Ньютона – Котеса.

Квадратурные формулы Ньютона-Котеса – большая группа формул, основанных на интерполяции подынтегральных функций.

Пусть – множество точек принадлежащих интервалу интегрирования .

С помощью этого множества задаются узлы интерполяции: , расположенные на интервале интегрирования . По указанным узлам интерполяции строится интегральный многочлен:

Интеграл заменяется приближенным интегралом: .

Ошибка численного интегрирования:

Из теории известно, что

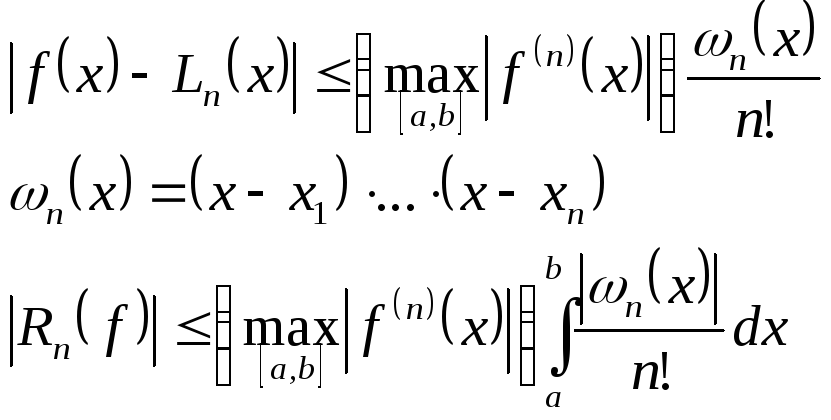
– фиксированный многочлен

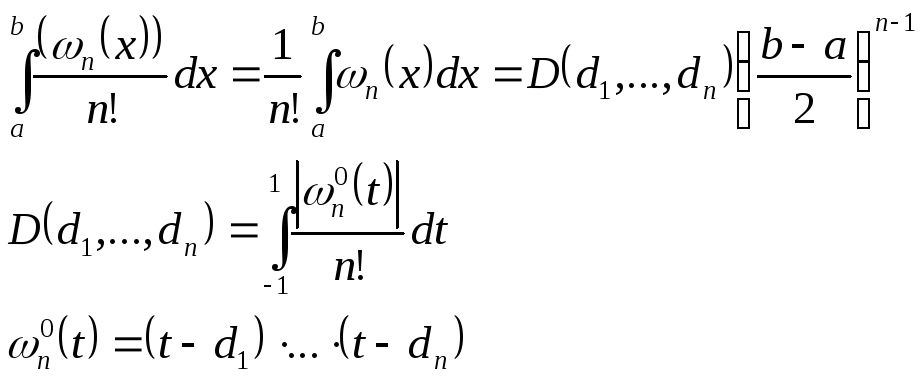
При этом квадратурная формула записывается в виде:

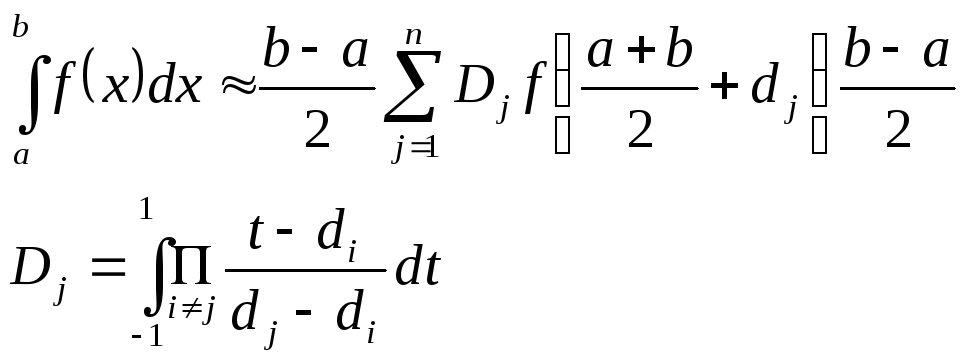
Формула, полученная методом интерполяции зависит от того, является ли число узлов четным или нечетным, а также зависит от формы весовой функции, которая может введена в эти уравнения.

20. Формулы прямоугольника, трапеций и Симпсона.

I. Формула прямоугольников

Число узлов , середина интервала

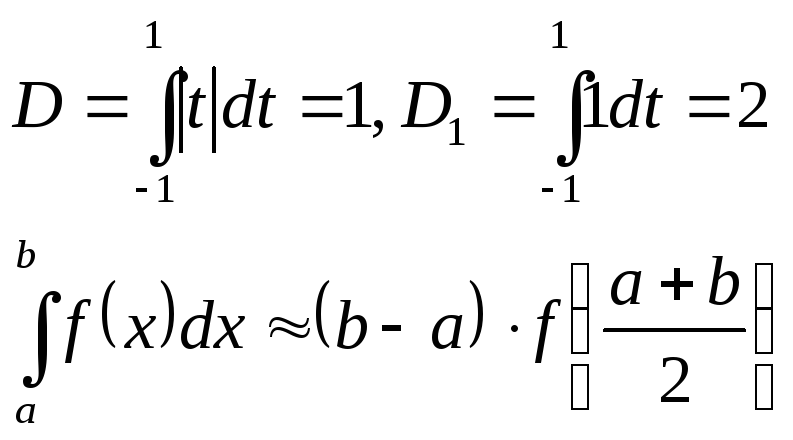
II. Формула трапеций

Число узлов , узлы располагаются в точках

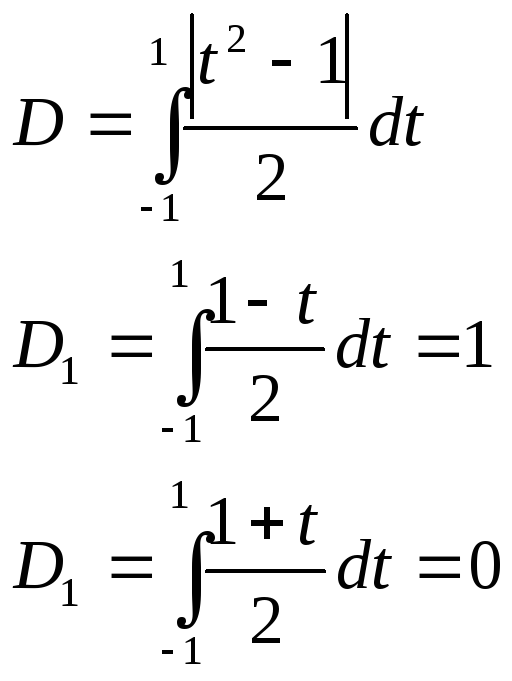
Получим квадратурную формулу:

III. Формула прямоугольников, как формула с кратным узлом

Кратным узлом трапеции называется узел, в котором задается не только значение функции, но и значения некоторого числа его производных.

Интерполяционная функция, в которой используются как значения самой функции, так и значения некоторого числа ее производных, называется формулой Эрмита.

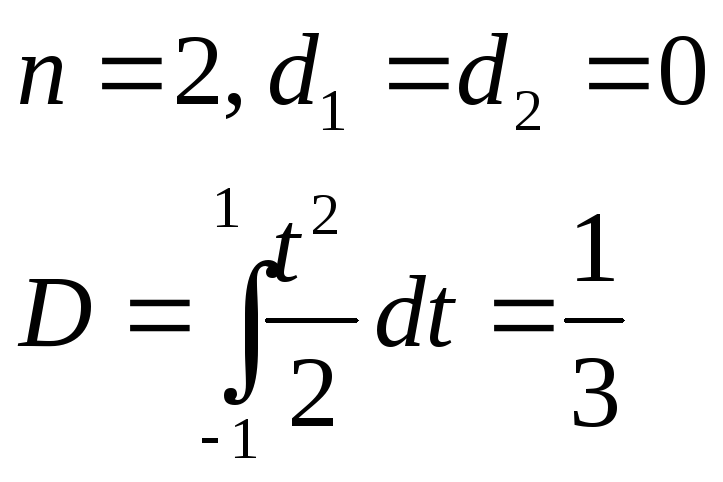
Квадратурная формула принимает вид:

Формула Симпсона получается методом интерполяции при следующих параметрах:

.