31. Методы Рунге – Кутта. Формулы Эйлера и Адамса.
Пусть требуется
численно решить задачу Коши для
дифференциального уравнения
(1)
при заданном
начальном условии
(2)
Зададим некоторый
достаточно малый шаг сетки вычислений
h.
Тогда для каждого
значение искомой функции (решения задачи
(1)-(2)) можно последовательно вычислить
по формуле Эйлера
Формула Эйлера является достаточно простой для программирования, однако, ее погрешность достаточно велика и сильно зависит от величины h.
Более точной
является неявная формула Адамса:
,
где значение
вычисляется по формуле Эйлера.
При использовании описанных формул следует учитывать, что погрешность увеличивается с каждым шагом вычислений.
32.Конечно-разностные методы решения задачи Коши.
Конечно-разностные методы – методы, в которых значения функции в конце каждого интервала зависят, в общем случае, от значений функции в конце предшествующих интервалов.
Разностные уравнения:
1)
В этом случае, уравнения называются явным или экстраполяционным.
К этому виду относится формула Эйлера.
В этом случае каждое значение
выражается через значение предшествующей
функции.
При
,
в правой части отсутствует.
2)
Это уравнение называется неявным или интерполяционным.
В этом случае искомое значение
входит в уравнение нелинейным образом,
или для его нахождения, в общем случае,
требуется применение итерационных
методов.
К этому классу относится формула Адамса, основанная на трапеции.
Существует также множество других методов, к которым относятся методы неопределенных коэффициентов и т.д.
Методы решения дифференциальных уравнений первого порядка практически без изменения переносятся на случай систем линейных дифференциальных уравнений первого порядка:
Отличие заключается в том, что вместо производных по скалярным переменным появляются производные по векторным переменным.
Метод Эйлера для этой системы записывается в виде:
Верхний индекс обозначает номер итерации.
Это будет система уравнений первого порядка.
33. Явные формулы Адамса.
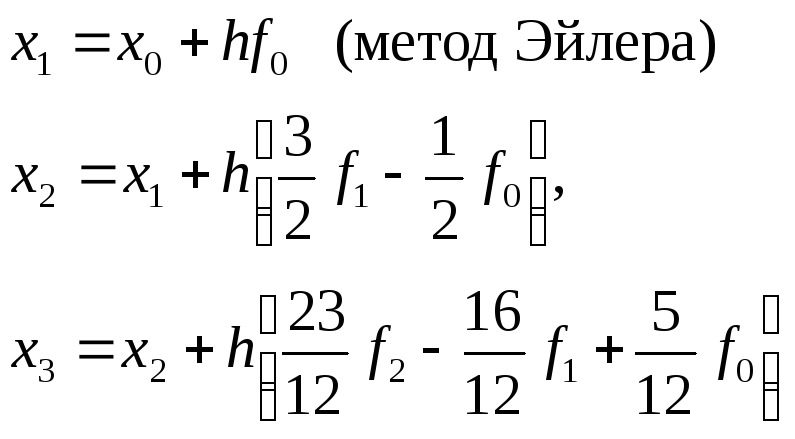
Формулы Адамса получаются при
интегрировании интерполяционного
многочлена
от
до
т.е. вне интервала интерполяции. Однако,
как мы знаем, вне этого интервала
интерполяционный многочлен обычно дает
довольно плохое приближение. Таким
образом, явные методы Адамса не очень
точны.
34. Решение задачи Коши методом неопределенных коэффициентов.
Воспользуемся методом неопределённых коэффициентов. Будем искать решение дифференциального уравнения в виде полинома:
его первая производная:
Заметим, что
.
Вычислим эти коэффициенты, подставив
начальные условия в исходное уравнение:
следовательно,
Для разложения логарифмической функции используем эталонный ряд:
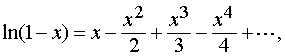
Преобразовав его, имеем
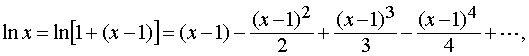где
.
В левой части уравнения получим очевидное
равенство:
,
и для краткости записи обозначим
;
уравнение примет вид:
.
Теперь подставляем в обе части
дифференциального уравнения вместо у
и
соответствующие полиномы, учитывая,
что
:
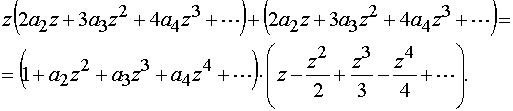
Приравниваем коэффициенты при одинаковых степенях z в левой и правой частях равенства, причём в правой части предварительно надо найти произведение двух рядов, затем решаем полученную систему уравнений:
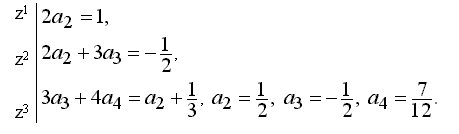
Подставляя все найденные коэффициенты в полином, получаем искомое решение задачи Коши:
