
- •1. Источники и виды погрешностей. Абсолютная и относительная погрешности. Вычислительная погрешность и погрешность функции.
- •3. Решение систем линейных алгебраических уравнений. Правило Крамера и обратная матрица. Вычислительная сложность.
- •4. Решение систем линейных уравнений. Метод исключения Гаусса с верхней и нижней треугольной матрицами. Методы прямой и обратной подстановки. Решение линейных систем алгебраических уравнений
- •Метод исключения Гаусса без перестановки строк
- •5. Решение систем линейных уравнений с симметричными и положительно определенными матрицами. Разложение Холесского с внутренним произведением.
- •6. Разложение Холесского с внешним произведением и с поблочным вычислением матриц.
- •Доказательство теоремы Халецкого
- •7. Метод исключения Гаусса и lu-разложение. Понятие эквивалентности систем уравнений, понятие и состав элементарных операций.
- •8. Алгоритм исключения Гаусса без перестановки строк. Lu- и ldv-разложения.
- •9. Алгоритм исключения Гаусса при наличии вырожденных главных подматриц. Алгоритм с перестановкой строк или с выбором главного элемента.
- •10. Свойства и определения матричных и векторных норм. Теорема Коши – Шварца. Число обусловленности системы линейных уравнений. Геометрический смысл числа обусловленности. Матричная норма
- •Геометрический смысл плохо обусловленных и хорошо обусловленных матриц
- •11. Задачи приближения и интерполяции функций и эмпирических данных.
- •13. Формулы численного дифференцирования интерполяционным методом.
- •14. Формулы численного дифференцирования методом неопределенных коэффициентов.
- •15. Наиболее распространенные формулы численного дифференцирования.
- •16. Задачи и методы численного интегрирования. Квадратурные формулы.
- •Элементарные квадратурные формулы, полученные методом интерполяции
- •17. Численное интегрирование интерполяционными методами.
- •18. Численное интегрирование методом неопределенных коэффициентов.
- •Частные случаи
- •19. Квадратурные формулы Ньютона – Котеса.
- •20. Формулы прямоугольника, трапеций и Симпсона.
- •21. Ортогональные и ортонормальные системы функций и многочленов. Скалярное произведение. Ортогонализация произвольной системы линейно независимых функций. Формула Грама – Шмидта.
- •22. Квадратурные формулы Гаусса. Наиболее распространенные формулы.
- •23. Интегрирование быстро осциллирующих функций. Интегрирование функций на больших интервалах изменения аргумента.
- •24. Тригонометрическая интерполяция и дискретное преобразование Фурье.
- •25. Быстрое преобразование Фурье.
- •26. Задача наименьших квадратов. Прямой метод решения.
- •27. Задача наименьших квадратов. Решение методом qr-разложения.
- •28. Алгоритм qr-разложения. Ортогональные матрицы и матрицы плоского вращения.
- •29. Задача численного решения обыкновенных дифференциальных уравнений. Задача Коши и граничные задачи.
- •30. Решение задачи Коши с помощью формулы Тейлора.
- •31. Методы Рунге – Кутта. Формулы Эйлера и Адамса.
- •32.Конечно-разностные методы решения задачи Коши.
- •33. Явные формулы Адамса.
- •34. Решение задачи Коши методом неопределенных коэффициентов.
- •35. Решение систем обыкновенных дифференциальных уравнений методом Эйлера.
- •36. Определение градиента функции нескольких переменных.
- •Метод градиента
- •37. Матрица Якоби системы функций нескольких переменных.
- •38. Решение нелинейных уравнений методом простой итерации.
- •39. Решение нелинейных уравнений методом Ньютона.
- •46. Необходимые и достаточные условия минимума и максимума функции многих переменных. Необходимые и достаточные условия экстремума функции нескольких (двух) переменных
- •47. Форма функции многих переменных в окрестности точки седла.
- •48. Градиентный метод минимизации функции многих переменных.
- •49. Минимизация функции многих переменных методом Ньютона.
- •Применительно к задачам оптимизации
- •50. Формула и множители Лагранжа в задаче оптимизации
- •Описание метода
- •51. Производная по направлению и возможное направление спуска.
- •52. Обратные и некорректные задачи.
37. Матрица Якоби системы функций нескольких переменных.
Матрица Якоби – матрица частных производных:
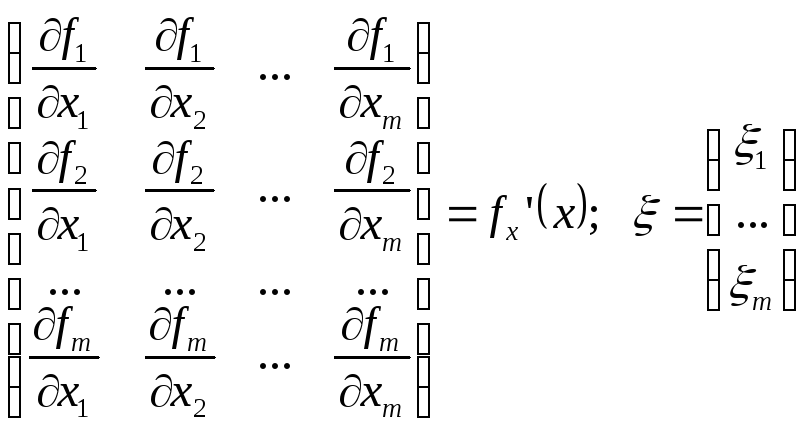
В матричной форме разложение системы функций в ряд Тейлора можно записать в виде:
![]()
Пусть
![]() – решение задачи
– решение задачи
![]()
x – точка, относительно которой осуществляется разложение в ряд Тейлора.
Пусть
![]() – значение вектора, полученного на
итерации номер n.
– значение вектора, полученного на
итерации номер n.
![]()
Получаем уравнение:
![]()
![]() – итерационное уравнение метода Ньютона.
– итерационное уравнение метода Ньютона.
![]() – номер итерации
– номер итерации
38. Решение нелинейных уравнений методом простой итерации.
В этом методе искомая система уравнений
записывается в виде
![]() .
.
Итерационная процедура строится в
соответствии с уравнением:
![]()
Алгоритм этой процедуры:
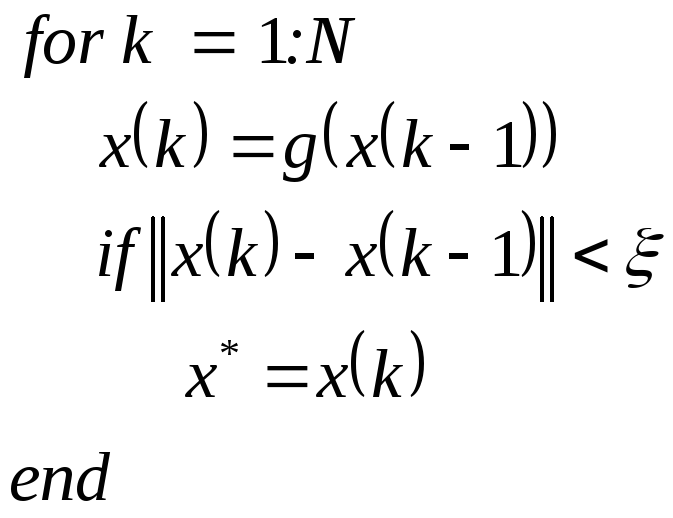
Условие сходимости простых итераций к решению:
если отображение
![]() является сжимающим, то уравнение
является сжимающим, то уравнение
![]() имеет единственное решение
имеет единственное решение
![]() ,
а расстояние между точным решением
,
а расстояние между точным решением
![]()
Расстоянием между двумя векторами называется функция, удовлетворяющая условиям:
1)
![]()
2)
![]()
3) неравенство треугольника:
![]()
Отображение
![]() называется сжимающим, если для любых
двух векторов
называется сжимающим, если для любых
двух векторов
![]() и
и
![]() расстояние между их отображениями
расстояние между их отображениями
![]() .
.
Доказательство теоремы сходимости простой итерации
![]()
![]() – вектор, полученный на n-ой
итерации.
– вектор, полученный на n-ой
итерации.
![]()
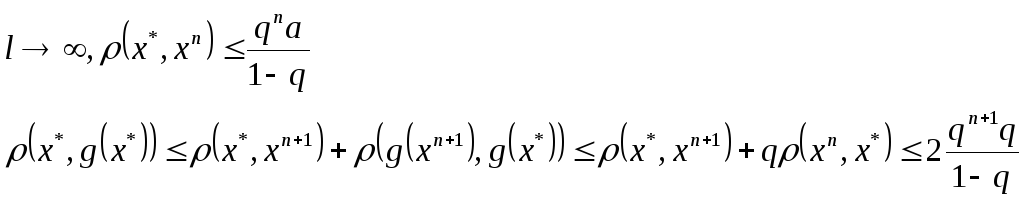 Доказательство
единственности решения осуществляется
методом от противного:
Доказательство
единственности решения осуществляется
методом от противного:
Примем, что существует два решения:
![]()
Расстояние между этими векторами:
![]()
Приходим к противоречию, поэтому вынуждены признать, что решение является единственным.
Геометрическая интерпретация простой итерации – функция одной переменной
![]()
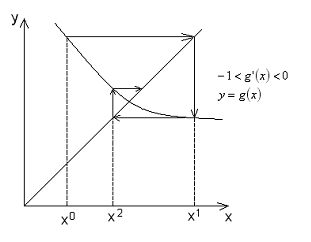
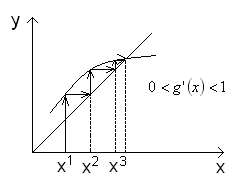
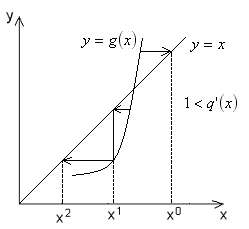
Интерполяционный процесс не сходится.
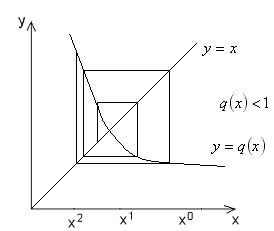
Можно показать, что в этих двух случаях
отображение
![]() является сжимающим.
является сжимающим.
При использовании метода простых
итераций для обеспечения сходимости
можно использовать различные способы
перехода от системы уравнений
![]() к системе
к системе
![]() .
.
39. Решение нелинейных уравнений методом Ньютона.
Идея метода Ньютона заключается в том, что нелинейная задача в окрестности некоторой точки заменяется на линейную задачу.
![]()
Запишем уравнение Тейлора в окрестности f(x)
![]()
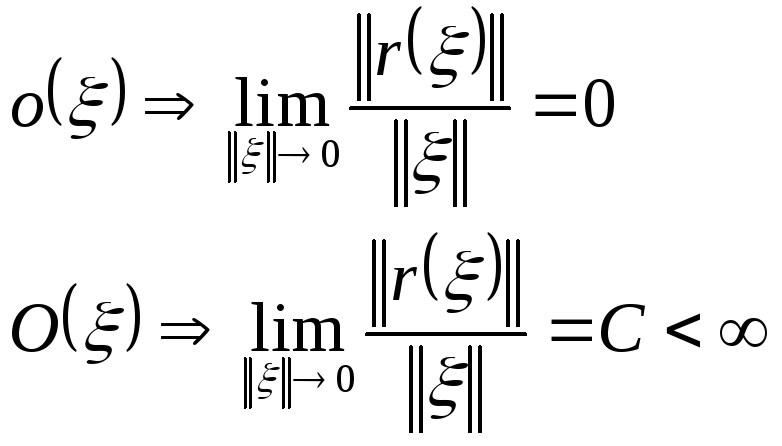
Введем матрицу частных производных:
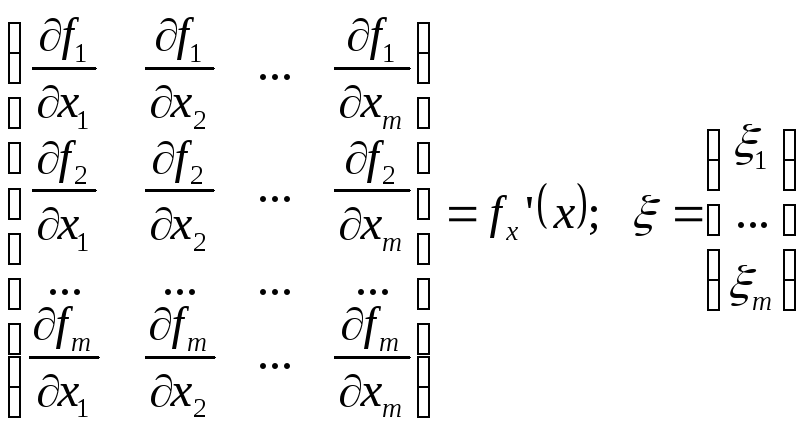
Эта матрица называется матрицей Якоби.
В матричной форме разложение системы функций в ряд Тейлора можно записать в виде:
![]()
Пусть
![]() – решение задачи
– решение задачи
![]()
x – точка, относительно которой осуществляется разложение в ряд Тейлора.
Пусть
![]() – значение вектора, полученного на
итерации номер n.
– значение вектора, полученного на
итерации номер n.
![]()
Получаем уравнение:
![]()
![]() – итерационное уравнение метода Ньютона.
– итерационное уравнение метода Ньютона.
![]() – номер итерации
– номер итерации
Метод Ньютона обеспечивает высокую скорость сходимости к решению, однако, требует, чтобы начальное значение x0 было достаточно близко к решению задачи. Поэтому иногда метод Ньютона сочетают с другими более грубыми методами, при этом грубые методы используются для нахождения стартовой точки метода Ньютона.
Сходимость алгоритма метода Ньютона, как и других методов, зависит не только от вида функции, но и от выбора начальной точки итерационного процесса.
46. Необходимые и достаточные условия минимума и максимума функции многих переменных. Необходимые и достаточные условия экстремума функции нескольких (двух) переменных
Рассмотрим
функцию ![]() ,
где
,
где ![]() --
открытое множество.
--
открытое множество.
Определение 1. ![]() называется
точкой максимума (минимума) функции
называется
точкой максимума (минимума) функции ![]() ,
если
,
если
![]()
Аналогично если выполняется строгое неравенство, точка называется точкой строгого максимума (строгого минимума).
Теорема 1. (необходимое
условие экстремума) Если ![]() --
точка экстремума и существует
--
точка экстремума и существует ![]() ,
то
,
то 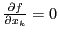 .
.
Определение 2. ![]() --
стационарная точка функции
--
стационарная точка функции ![]() ,
если
,
если ![]() --
дифференцируема в этой точке и
--
дифференцируема в этой точке и 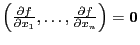 ,
или
,
или ![]() --
не дифференцируема в этой точке.
--
не дифференцируема в этой точке.
Замечание 1. Квадратичная
форма -- многочлен вида ![]() ,
, ![]() --
положительно определена, если на
положительных переменных она принимает
положительные значения. Для квадратичных
форм существует критерий Сильвестра:
форма положительно определена, если
все главные миноры ее матрицы положительны.
Форма отрицательно определена,
если
--
положительно определена, если на
положительных переменных она принимает
положительные значения. Для квадратичных
форм существует критерий Сильвестра:
форма положительно определена, если
все главные миноры ее матрицы положительны.
Форма отрицательно определена,
если ![]() положительно
определена. Тогда главные миноры меняют
знак, начиная с минуса.
положительно
определена. Тогда главные миноры меняют
знак, начиная с минуса.
Теорема 2. (достаточное
условие экстремума) Если ![]() дважды
дифференцируема в стационарной точке
дважды
дифференцируема в стационарной точке ![]() ,
то
,
то ![]() --
точка минимума (максимума), если
квадратичная форма
--
точка минимума (максимума), если
квадратичная форма ![]() положительно
(отрицательно) определена. Если эта
форма не определена, то экстремума в
этой точке нет. Если она вырождена, то
неизвестно, является ли
положительно
(отрицательно) определена. Если эта
форма не определена, то экстремума в
этой точке нет. Если она вырождена, то
неизвестно, является ли ![]() точкой
экстремума.
точкой
экстремума.
Замечание 2. В
случае двух переменных матрица
квадратичной формы имеет вид  .
Тогда если
.
Тогда если ![]() ,
то для положительной определенности
достаточно
,
то для положительной определенности
достаточно ![]() --
тогда имеется минимум. Если же
--
тогда имеется минимум. Если же ![]() ,
то достигается максимум. Если же
,
то достигается максимум. Если же ![]() ,
то ничего сказать нельзя.
,
то ничего сказать нельзя.
