26. Задача наименьших квадратов. Прямой метод решения.

Задача наименьших квадратов, возникающая при научных и инженерных расчетах, может рассматриваться, как задача восстановления зависимости по эмпирическим данным.

Эмпирические данные представляют собой значения неизвестной функции, полученные в результате эксперимента на сетке узлов, в общем случае, неравномерной.

Узлы сетки могут представлять собой моменты времени или пространственные координаты линейной электрической или механической системы.

Координаты узлов и значения функции в этих узлах объединяются в набор точек , где – координаты узлов, – значения функции.

Задача заключается в определении коэффициентов аппроксимирующей функции, которая должна приближать наблюдаемые данные с возможно большей точностью.

Пример: . Такая функция часто используется при отслеживании дрейфа временных рядов в экономике.

В общем случае такая функция может не обеспечить требуемую точность восстановления зависимости. Поэтому в качестве аппроксимирующих функций используются общие многочлены по системе линейно-независимых функций:

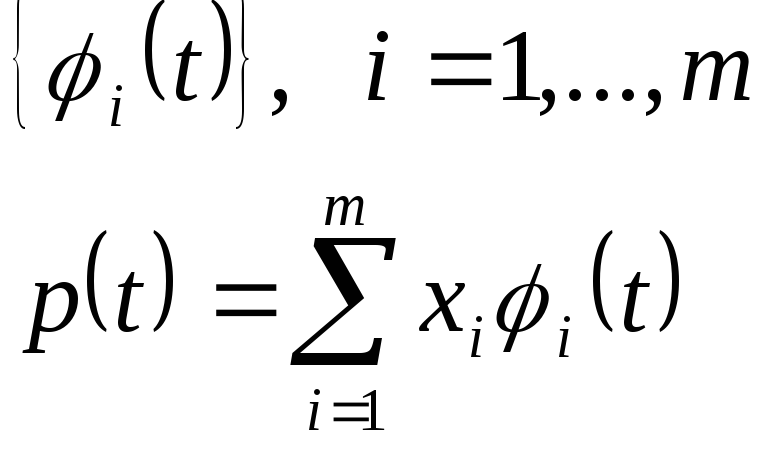
Система независимых функций, которая называется системой, может быть представлена в виде степенных функций, тригонометрических функций и др.

В случае степенных функций .

Число базисных функций и размерность пространства базисных функций, как правило, меняет число наблюдаемых данных.

В идеале, желательно, что бы ошибки в узлах сетки имели минимальную величину: .

Если потребовать, чтобы ошибки в узлах сетки были равны нулю, то коэффициенты обобщенного многочлена должны удовлетворять матричному уравнению:

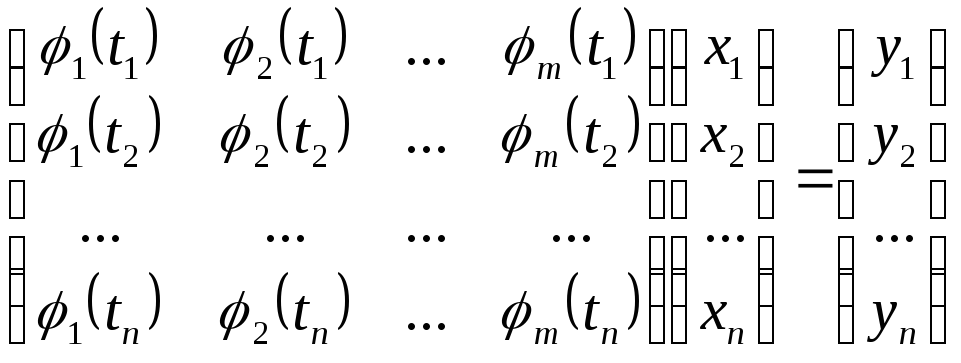
Решения этой системы возможно только при условии, если , и определитель матрицы отличен от нуля: , в противном случае решение этой системы оказывается невозможным. Однако, можно подобрать такие значения коэффициентов многочлена, чтобы полученный многочлен приближал наблюдаемые данные к значениям функции.

Точность восстановления зависимости, представленной вектором невязок 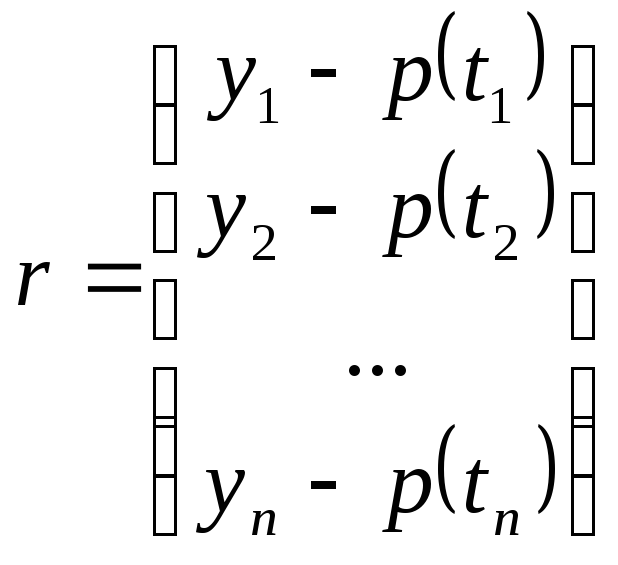можно представить некоторой нормой, которая характеризует среднее значение ошибок по всем узлам.

В качестве нормы можно использовать выражение:

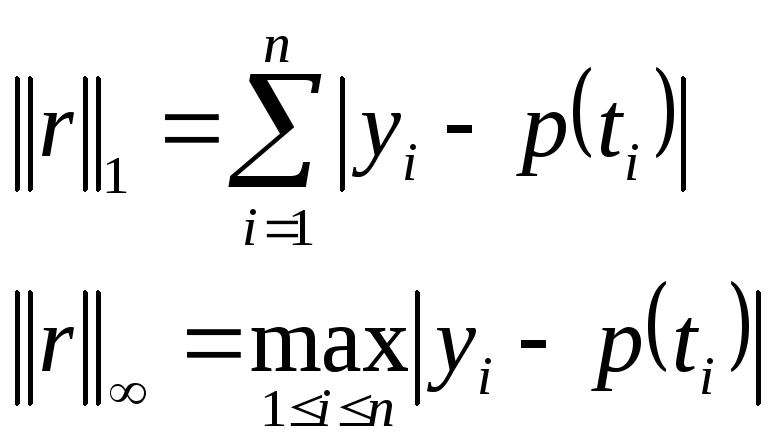
Евклидова норма: или квадрат этой нормы: .

Задача наименьших квадратов возникает из задачи минимизации квадрата евклидовой нормы

Прямой подход к решению задачи минимизации квадрата евклидовой нормы сводится к нахождению коэффициентов, при которых градиент вектора нормы невязки равен нулю.

Градиент функции обозначается оператором Набла.

Градиент функции – вектор первых частных производных функции по компонентам вектора.

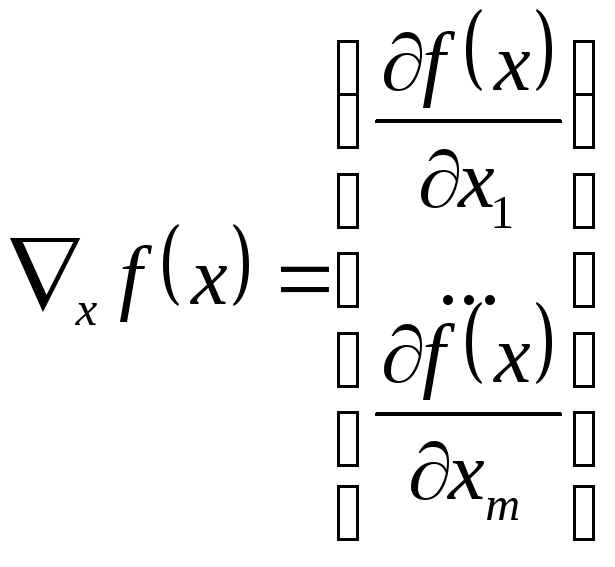
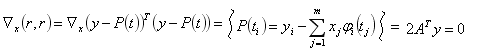
Получим систему линейных алгебраических уравнений:

Решение этой системы сводится к нахождению обратной матрицы:

При большой размерности пространства базисных функций, нахождение обратной матрицы является достаточно трудоемкой задачей.

Чтобы преодолеть эту проблему, численные методы решения задачи наименьших квадратов основываются на разложении матриц исходной системы.

Одним из эффективных методов решения задачи является метод QR-разложения.

По этому методу исходная матрица системы уравнений разлагается в произведение матриц: .

Матрица A считается квадратной, если квадратными являются матрицы Q и R.

Матрица Q – ортогональная матрица, а матрица R – верхняя треугольная матрица.

Матрица называется ортогональной, если:

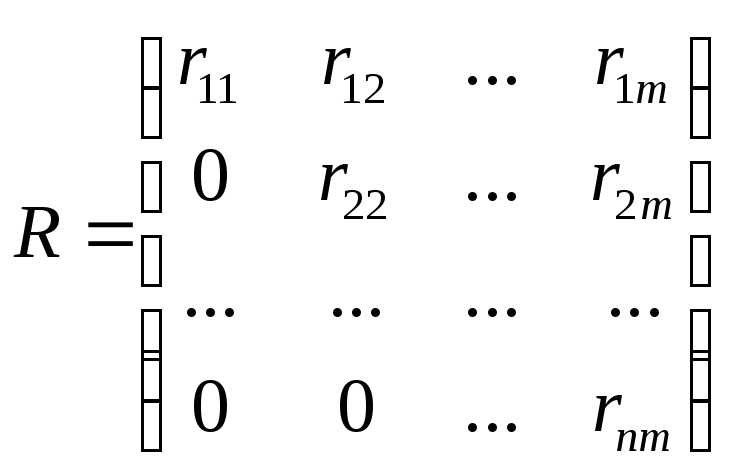
Разложение матрицы A в произведение ортогональной и верхней треугольной матриц позволяет решить алгебраическую систему уравнений в два этапа.

1)

получим систему:

решение системы:

2)

эту систему можно решить методом обратной подстановки.