
- •1. Источники и виды погрешностей. Абсолютная и относительная погрешности. Вычислительная погрешность и погрешность функции.
- •3. Решение систем линейных алгебраических уравнений. Правило Крамера и обратная матрица. Вычислительная сложность.
- •4. Решение систем линейных уравнений. Метод исключения Гаусса с верхней и нижней треугольной матрицами. Методы прямой и обратной подстановки. Решение линейных систем алгебраических уравнений
- •Метод исключения Гаусса без перестановки строк
- •5. Решение систем линейных уравнений с симметричными и положительно определенными матрицами. Разложение Холесского с внутренним произведением.
- •6. Разложение Холесского с внешним произведением и с поблочным вычислением матриц.
- •Доказательство теоремы Халецкого
- •7. Метод исключения Гаусса и lu-разложение. Понятие эквивалентности систем уравнений, понятие и состав элементарных операций.
- •8. Алгоритм исключения Гаусса без перестановки строк. Lu- и ldv-разложения.
- •9. Алгоритм исключения Гаусса при наличии вырожденных главных подматриц. Алгоритм с перестановкой строк или с выбором главного элемента.
- •10. Свойства и определения матричных и векторных норм. Теорема Коши – Шварца. Число обусловленности системы линейных уравнений. Геометрический смысл числа обусловленности. Матричная норма
- •Геометрический смысл плохо обусловленных и хорошо обусловленных матриц
- •11. Задачи приближения и интерполяции функций и эмпирических данных.
- •13. Формулы численного дифференцирования интерполяционным методом.
- •14. Формулы численного дифференцирования методом неопределенных коэффициентов.
- •15. Наиболее распространенные формулы численного дифференцирования.
- •16. Задачи и методы численного интегрирования. Квадратурные формулы.
- •Элементарные квадратурные формулы, полученные методом интерполяции
- •17. Численное интегрирование интерполяционными методами.
- •18. Численное интегрирование методом неопределенных коэффициентов.
- •Частные случаи
- •19. Квадратурные формулы Ньютона – Котеса.
- •20. Формулы прямоугольника, трапеций и Симпсона.
- •21. Ортогональные и ортонормальные системы функций и многочленов. Скалярное произведение. Ортогонализация произвольной системы линейно независимых функций. Формула Грама – Шмидта.
- •22. Квадратурные формулы Гаусса. Наиболее распространенные формулы.
- •23. Интегрирование быстро осциллирующих функций. Интегрирование функций на больших интервалах изменения аргумента.
- •24. Тригонометрическая интерполяция и дискретное преобразование Фурье.
- •25. Быстрое преобразование Фурье.
- •26. Задача наименьших квадратов. Прямой метод решения.
- •27. Задача наименьших квадратов. Решение методом qr-разложения.
- •28. Алгоритм qr-разложения. Ортогональные матрицы и матрицы плоского вращения.
- •29. Задача численного решения обыкновенных дифференциальных уравнений. Задача Коши и граничные задачи.
- •30. Решение задачи Коши с помощью формулы Тейлора.
- •31. Методы Рунге – Кутта. Формулы Эйлера и Адамса.
- •32.Конечно-разностные методы решения задачи Коши.
- •33. Явные формулы Адамса.
- •34. Решение задачи Коши методом неопределенных коэффициентов.
- •35. Решение систем обыкновенных дифференциальных уравнений методом Эйлера.
- •36. Определение градиента функции нескольких переменных.
- •Метод градиента
- •37. Матрица Якоби системы функций нескольких переменных.
- •38. Решение нелинейных уравнений методом простой итерации.
- •39. Решение нелинейных уравнений методом Ньютона.
- •46. Необходимые и достаточные условия минимума и максимума функции многих переменных. Необходимые и достаточные условия экстремума функции нескольких (двух) переменных
- •47. Форма функции многих переменных в окрестности точки седла.
- •48. Градиентный метод минимизации функции многих переменных.
- •49. Минимизация функции многих переменных методом Ньютона.
- •Применительно к задачам оптимизации
- •50. Формула и множители Лагранжа в задаче оптимизации
- •Описание метода
- •51. Производная по направлению и возможное направление спуска.
- •52. Обратные и некорректные задачи.
21. Ортогональные и ортонормальные системы функций и многочленов. Скалярное произведение. Ортогонализация произвольной системы линейно независимых функций. Формула Грама – Шмидта.
Если
![]() – система линейно-независимых функций:
– система линейно-независимых функций:
![]() ,
принадлежащих пространству H:
,
принадлежащих пространству H:
![]() ,
то существует система независимых
ортогональных функций:
,
то существует система независимых
ортогональных функций:
![]() ,
каждая из которых может быть представлена
в виде линейной комбинации линейной
системы:
,
каждая из которых может быть представлена
в виде линейной комбинации линейной
системы:
![]() .
.
Условие ортогонализации:
![]() .
.
Доказательство:
оно является конструктивным, т.е. основывается на построении алгоритма нахождения ортогональных функций по исходной системе независимых функций.
Первая функция ортогональной системы.
Пусть
![]()
Из условия ортогонализации:
![]() ,
,
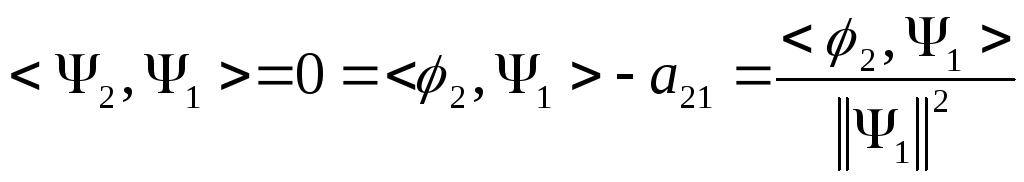
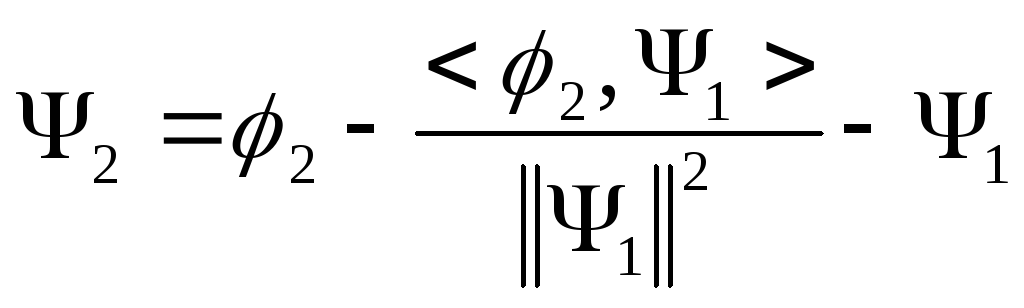
На каком-то шаге получим ортогональные
функции:
![]() ,
,
![]() .
.
Коэффициенты этой линейной комбинации
определяются из условия ортогонализации
![]() функции всем предшествующим функциям
системы.
функции всем предшествующим функциям
системы.
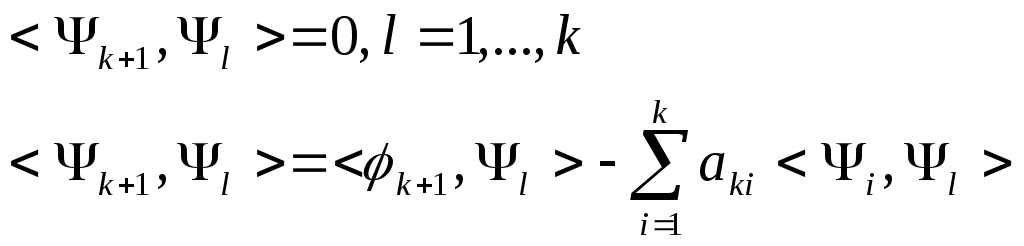
Система функций
![]() по условию ортогональна, значит,
по условию ортогональна, значит,
![]() ,
следовательно,
,
следовательно,
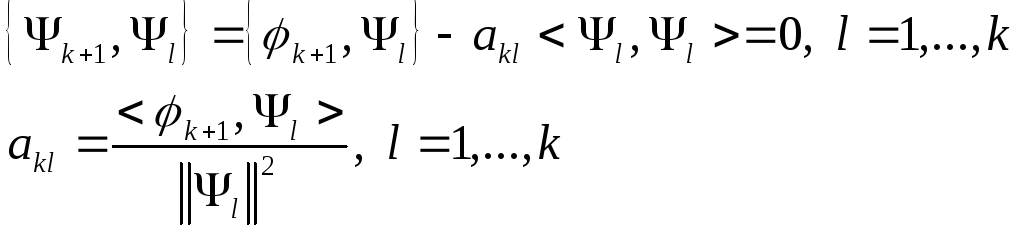
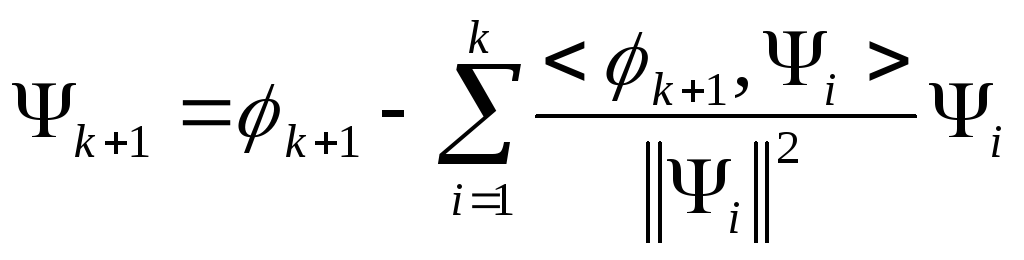
Процедура ортогонализации называется процедурой Грамма-Шмидта.
Все функции выражаются через старую
функцию, значит, все функции можно
представить в виде линейной комбинации
системы функций:
![]() .
.
Если представить исходную и ортогональную системы функций в виде векторов:
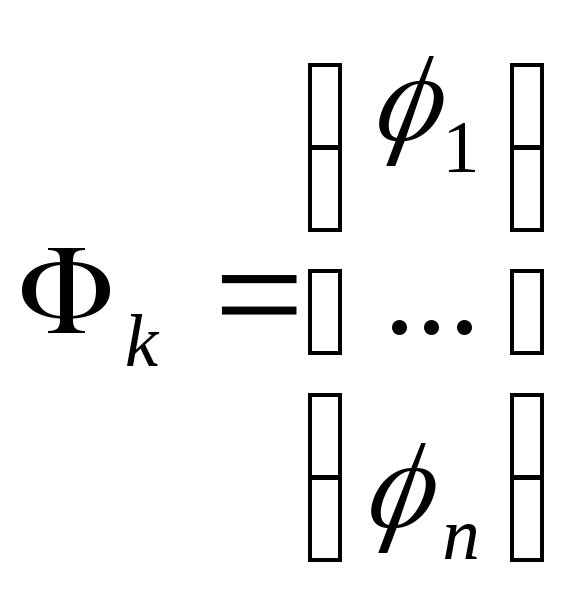 ,
,
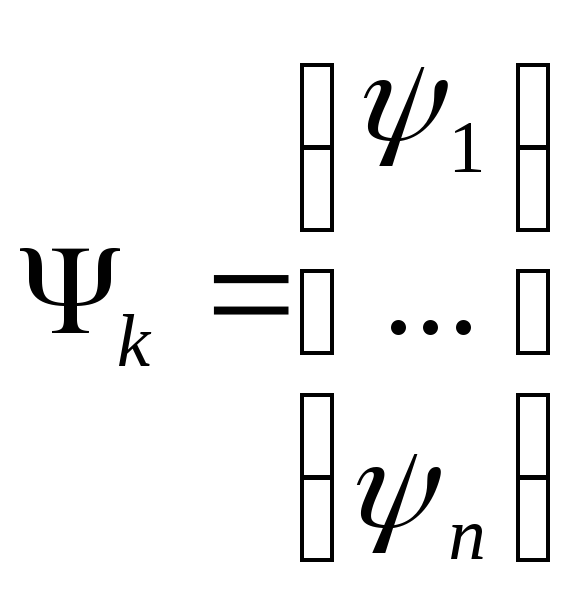 ,
,
то переходы к ортогональной система в
матричном виде:
![]() .
.
Матрица B является нижней унитарной матрицей:
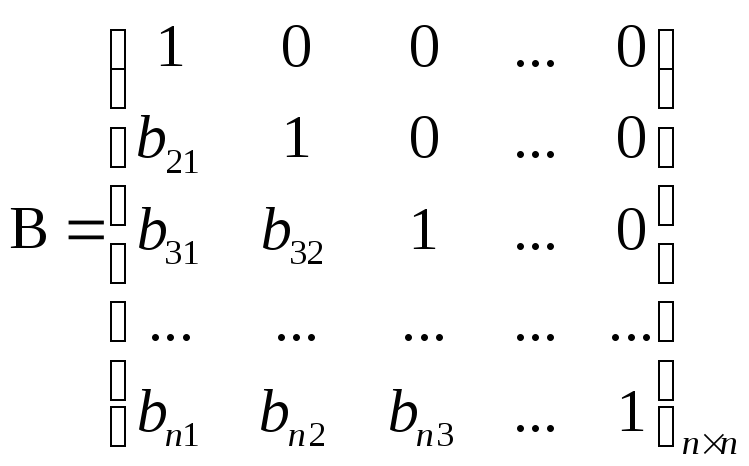
![]()
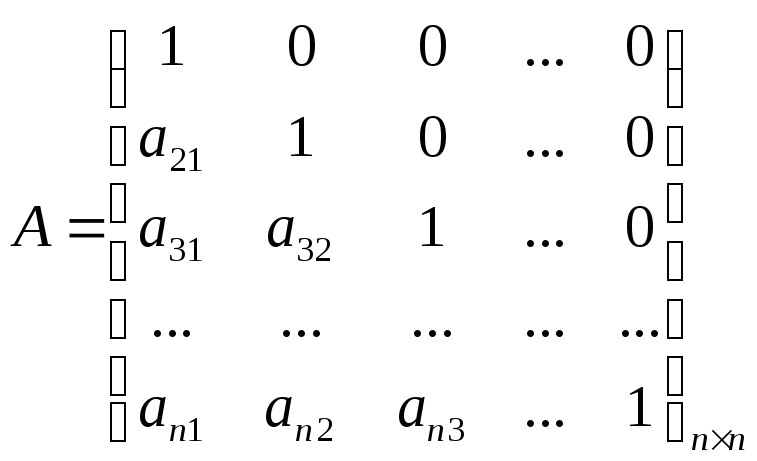
![]()
![]()
Коэффициенты матрицы A – коэффициенты, полученные в процессе ортогонализации.
При рассмотрении ортогональных многочленов в качестве независимой системы используется система степенных функций:
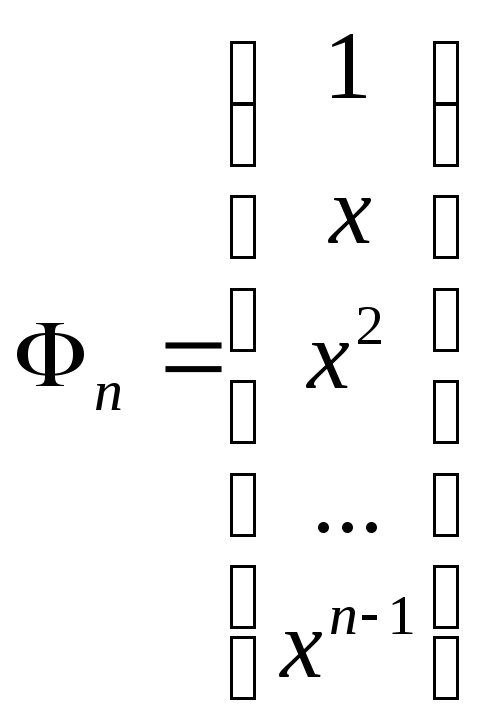
К ортогональным многочленам относятся многочлены Чебышева первого и второго рода. Ортогональные многочлены легко находятся с помощью рекуррентных формул.
Так многочлены Чебышева первого рода определяются:
![]()
Многочлены Чебышева первого рода
являются многочленами ортогональными
на интервале
![]() с весом
с весом
![]()
Условие ортогонализации:
![]()
Многочлены Чебышева второго рода можно найти по рекуррентной формуле:
![]()
Многочлены Чебышева второго рода
являются ортогональными на интервале
![]() с весом
с весом
![]() .
.
22. Квадратурные формулы Гаусса. Наиболее распространенные формулы.
Задачи построения квадратурной формулы Гаусса с n узлами заключается в решении задачи оптимизации, в рамках которой, квадратурная формула должна быть точной для любых многочленов в максимально возможной степени.
Неизвестными коэффициентами являются как коэффициенты квадратурной формулы, так и ее узлы.
![]()
![]() – коэффициенты квадратурной формулы
– коэффициенты квадратурной формулы
![]()
Число независимых переменных равно
![]() .
.
Число коэффициентов:
![]()
Если квадратурная формула является точной для многочлена степени n, то она является точной и для всех степеней переменной x.
![]()
1)
Квадратурные Гаусса
формулы —
формулы вида
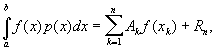 в которых узлы xk и
коэффициенты Ak не
зависят от функции f
(x) и
выбраны так, что формула точна (т. е. Rn =
0) для произвольного многочлена степени 2n
- 1. В отличие
от квадратурных формул Ньютона — Котеса,
узлы в квадратурных Гаусса
формулы,
вообще говоря, не являются равноотстоящими.
Если р
(х) ³ 0 и
в которых узлы xk и
коэффициенты Ak не
зависят от функции f
(x) и
выбраны так, что формула точна (т. е. Rn =
0) для произвольного многочлена степени 2n
- 1. В отличие
от квадратурных формул Ньютона — Котеса,
узлы в квадратурных Гаусса
формулы,
вообще говоря, не являются равноотстоящими.
Если р
(х) ³ 0 и
 то для любого натурального n имеется
единственная квадратурная Гаусса
формулы Эти
формулы имеют большое практическое
значение, т.к. в ряде случаев они дают
значительно большую точность, чем
квадратурные формулы с тем же числом
равноотстоящих узлов. Сам Гаусс исследовал
(1816) случай р
(х) º 1.
2) Гаусса
формулы,
выражающая полную
кривизну К
поверхности через коэффициенты её
линейного элемента; в координатах, для
которых ds2 =
l(du2 +
dv2), Гаусса
формулы имеет
вид
то для любого натурального n имеется
единственная квадратурная Гаусса
формулы Эти
формулы имеют большое практическое
значение, т.к. в ряде случаев они дают
значительно большую точность, чем
квадратурные формулы с тем же числом
равноотстоящих узлов. Сам Гаусс исследовал
(1816) случай р
(х) º 1.
2) Гаусса
формулы,
выражающая полную
кривизну К
поверхности через коэффициенты её
линейного элемента; в координатах, для
которых ds2 =
l(du2 +
dv2), Гаусса
формулы имеет
вид
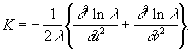 Эта формула была опубликована в 1827 и
показывает, что полная кривизна не
меняется при изгибании поверхности.
Она составляет содержание одного из
основных предложений созданной
Гауссом внутренней
геометрии поверхности.
3) Гаусса
формулы для
сумм Гаусса:
Эта формула была опубликована в 1827 и
показывает, что полная кривизна не
меняется при изгибании поверхности.
Она составляет содержание одного из
основных предложений созданной
Гауссом внутренней
геометрии поверхности.
3) Гаусса
формулы для
сумм Гаусса:
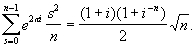 Эта формула была использована Гауссом
(1801) в одном из доказательств закона
взаимности квадратичных
вычетов
Эта формула была использована Гауссом
(1801) в одном из доказательств закона
взаимности квадратичных
вычетов
