2.3. Закони розподілу

У розділі 2.2 введено поняття «крива розподілу часу наробки до відмови», тобто залежність f(t). Ця залежність може служити математичною моделлю надійності виробу, необхідною для теоретичної оцінки надійності окремого елемента чи системи в цілому. Зрозуміло, що спектр різновидів функцій f(t) буде дуже широким, оскільки вони відбивають особливості фізичних процесів, властивих саме тому чи іншому виробові.

Маючи криву розподілу наробки до відмови, визначають всі інші характеристики надійності. З урахуванням (2.18) можна стверджувати, що кривою розподілу може бути будь-яка лінія, площа під якою дорівнює одиниці. Як свідчать численні дослідження, надійність більшості виробів може бути змодельована певною сукупністю функцій, які ми розглянемо далі. Вони дають змогу описати величину f(t) з максимальним наближенням до тих залежностей f'(t), які відбивають реальну природу виробів. Це є розподіли Вейбула, гама-розподіл та їх окремі випадки, якими дуже часто користуються, нормальний розподіл, логарифмічно-нормальний, альфа-розподіл, розподіл Релея, трикутний розподіл тощо. Коротке пояснення аналітичних виразів законів розподілів і області їх застосування в теорії надійності почнемо з розподілу Вейбула [З].

У цьому випадку

(2.51)

де С — параметр масштабу, який «стискає», чи «розтягує» криву;

 — параметр форми розподілу, який стискає його асиметрію і ексцес.

Графіки функції розподілу Вейбула показані на рис.2.4.

Запишемо ймовірність безвідмовної роботи для даного випадку

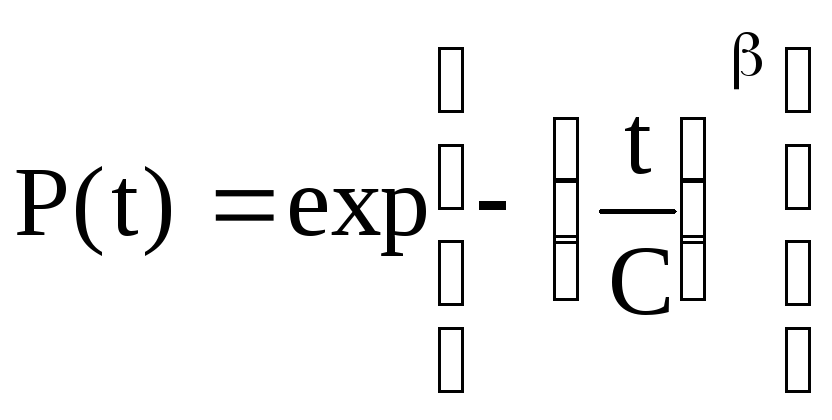(2.52)

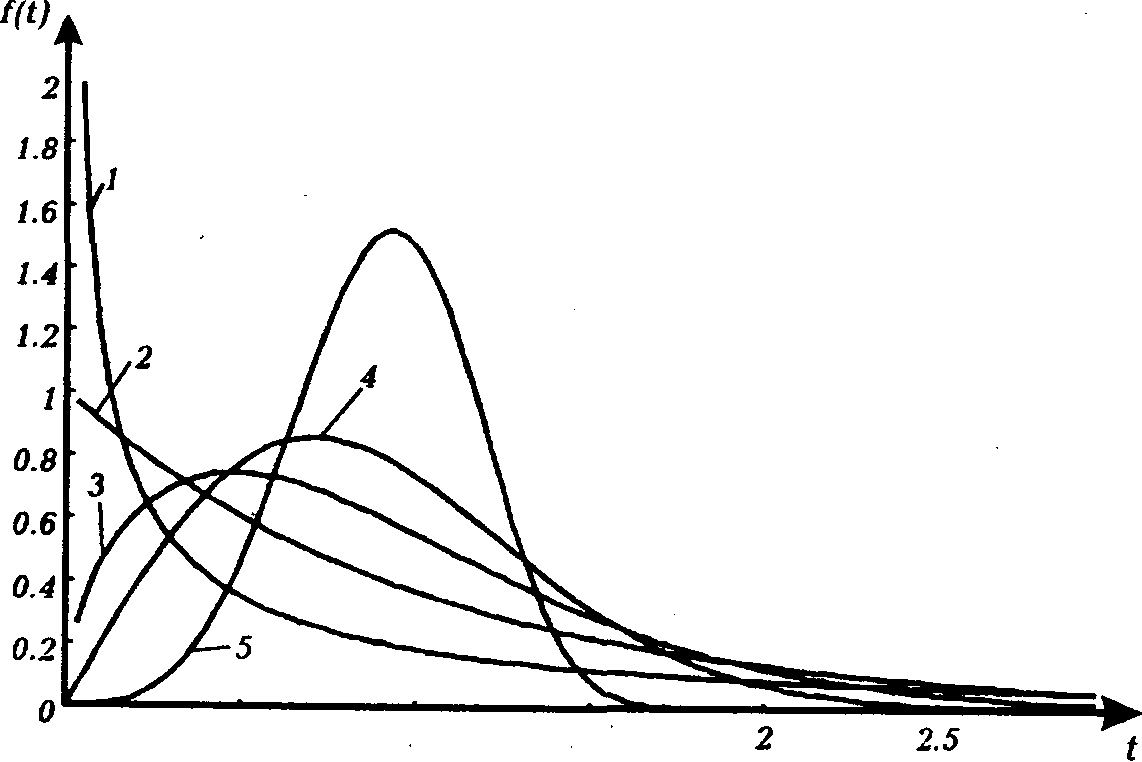
Рис.2.4. Графіки розподілу Вейбула при С=1 у випадках  = 0,5 (крива 1),  = 1 (крива 2),  = 1.5 (крива 3),  = 2 (крива 4),  = 4 (крива 5).

Своєю чергою інтенсивність відмов матиме вигляд:

(2.53)

Вирази (2.52) і (2.53) графічно зображені на рис.2.5.

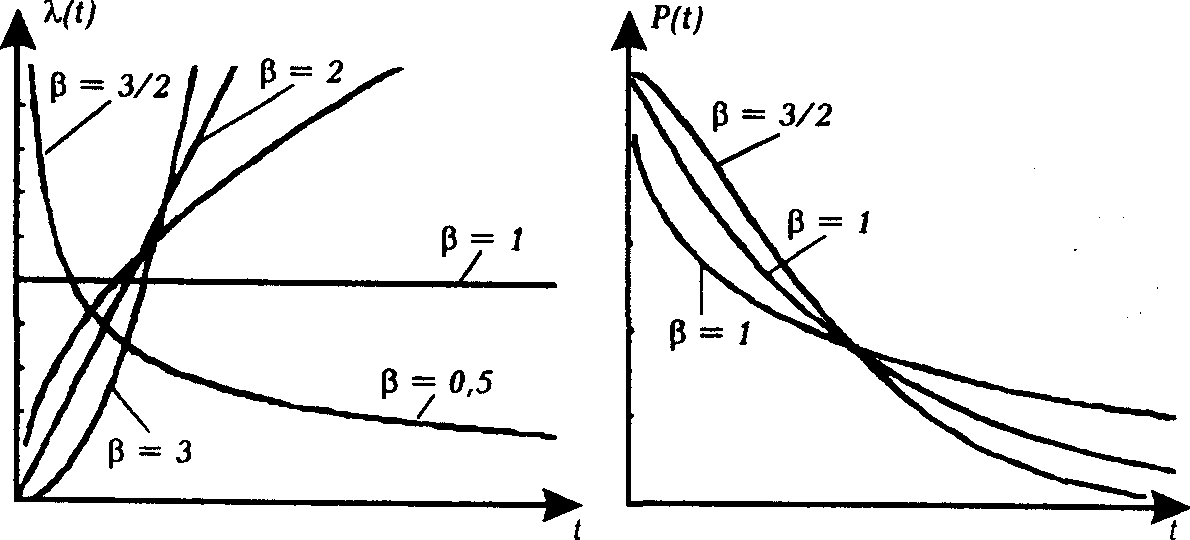
Рис.2.5. Криві інтенсивності відмов та ймовірності безвідмовної роботи при розподілі Вейбула.

Середній час наробки до відмови Т_м розраховують таким чином:

(2.54)

де - гама-функція, яку знаходять за таблицями в додатку 1.

Розподіл Вейбула використовують для отримання математичної моделі надійності деякого механічного обладнання, зокрема, підшипників, які застосовують в електричних двигунах, а також для окремих типів електронних ламп (р= 1,41,7).

Перевагою розподілу Вейбула є велика кількість форм кривих, які можна отримати. Це дає змогу використовувати даний закон розподілу для більш широкого класу електрооб- ладнання, ніж вказано вище, в початковий період експлуатації (період приробки).

Наступною моделлю густини розподілу часу наробки до відмови є гама-розподіл. У цьому випадку згадана густина розподілу має вигляд:

, , 0, t0 (2.55)

Такий розподіл також задається двома параметрами:  — параметр масштабу;  — параметр форми розподілу. Графічне зображення f(t) для гама-розподілу показано на рис.2.11. Середній час наробки до відмов у цьому випадку визначають як T_M =/.

У теорії надійності гама-розподіл використовується при цілих значеннях . Тоді гама-розподіл називається розподілом Ерланга [4]. Для розподілу Ерланга запишемо

(2.56)

Ймовірність безвідмовної роботи та інтенсивність відмов матиме вигляд

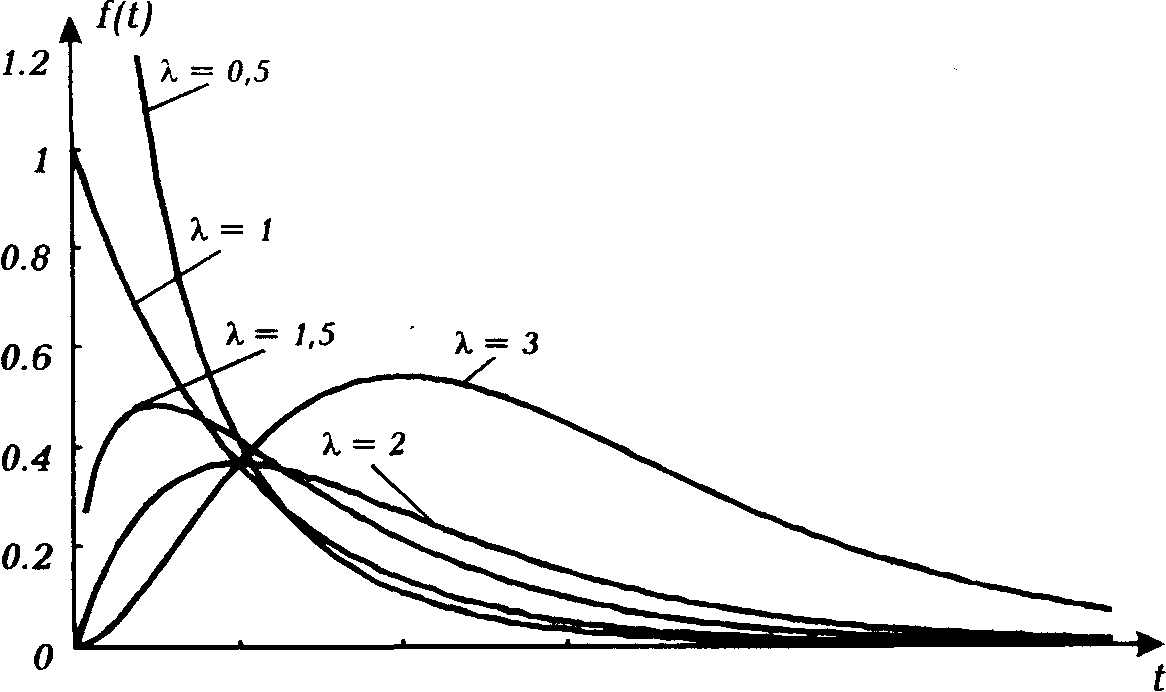
Рис. 2.6. Гама-розподіл при різних параметрах .

(2.57)

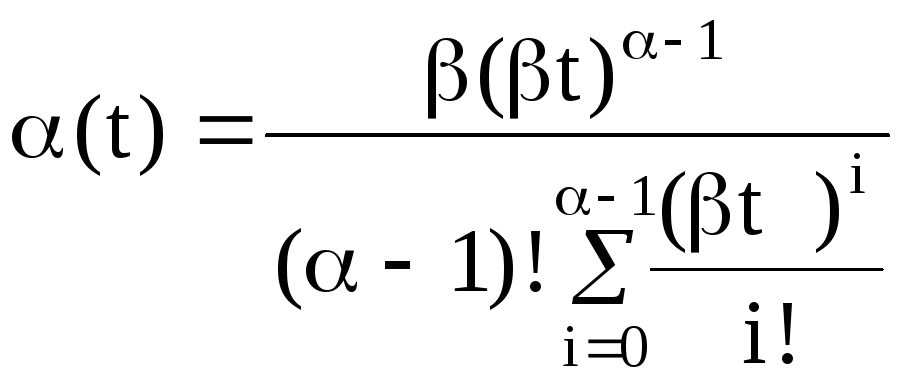(2.58)

Графіки залежностей f(t),P(t),(t) для розподилу Ерланга показані нав рис.2.7

Рис.2.7. Графіки функцій при розподілі Ерланга (1).

Розподіл Ерланга другого порядку ( = 1,  = 2/Т_в) широко використовують для моделювання розподілу часу відновлення систем електроприводів. Це пояснюється тим, що час відновлення t_в складається з двох частин:

t_В=t_o+t_p (2.59)

де t_o — час, затрачений на пошук несправностей;

t_p — час, затрачений на ремонт.

Якщо припустити, що випадкові величини t_o і t_p розподілені за експоненційним законом ((2.62) — (2.64)) з однаковими середніми значеннями Т_B/2, то густина ймовірності величини t_B, яка є комбінацією t_o і t_p відповідності з відомими положеннями теорії ймовірності:

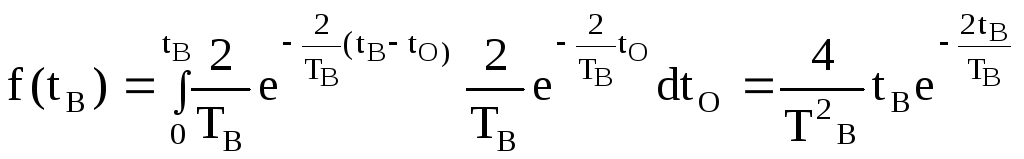(2.60)

Залежність f(t_B), побудована у відповідності з (2.60), відповідає графіку на рис.2.12 при  > 1, тобто має вигляд густини розподілу Ерланга.

Критерій ремонтопридатності — ймовірність відновлення системи за t_зв буде у відповідності з (2.49) дорівнювати:

(2.61)

Гама-розподіл також має великий спектр кривих. Особливістю такого розподілу є те, що сума n незалежних випадкових величин, кожна з яких підпорядковується гамарозподілу з параметрами  і ,також має гама-розподіл з параметрами  і

Розглянемо окремий випадок розподілу Вейбула (при  = 1) та гама-розподілу Ерланга (при  =1) — експоненційний розподіл.

Цей розподіл часу наробки до відмови характеризується виразами f(t), P(t), (t).

(t) =  = const, (2.62)

f(t)= exp(-t), (2.63) P(t)=exp(-t). (2.64)

Такий закон розподілу ще називають показниковим. Графіки функцій f(t), (t) і P(t) при експоненційному законі розподілу показані на рис.2.8.

.

Рис2.8. Графіки екпоненціального закону росподілу.

Наведений закон розподілу використовують доволі часто, оскільки він придатний для опису характеристик надійності склад них електромеханічних систем, навіть якщо елементи цих систем мають різноманітні закони розподілу. Це пояснюється тим, що більшість виробів проходить «тренування» безпосередньо після виготовлення в заводських умовах і до споживача вони надходять при стабільно низьких значеннях інтенсивностей відмов. Завдяки цьому споживач працює з виробами, які мають більш-менш постійні величини . Експоненційний розподіл також набув широкого поширення через простоту формул для розрахунку характе ристик надійності. При недостатній кількості статистичних дант складно виявити відхилення від виразу  = const, навіть якщо такі відхилення і відбувається. У цьому випадку постійне значення інтенсивності відмов можна прийняти як перше наближення при розрахунках. У той же час, якщо вироби не пройшли «тренування»на виробництві в початковий період експлуатації, розподіл часу наробки до відмови потребує іншої математичної моделі. Такою моделлю може бути нормальний закон розполілу.

Цей розподіл ще називають розподілом Гаусса. Оскільки час наробки до відмови набуває тільки додатних значень, то в теорії надійності йдеться про зрізаний нормальний розподіл.

Зрізаний нормальний розподіл отримують з нормального, обмежуючи інтервал значень випадкової величини часу наробки до відмови t₁  t₂. Тоді запишемо густину зрізаного нормального розподілу

f(t)=C f(t), (2.65)

де 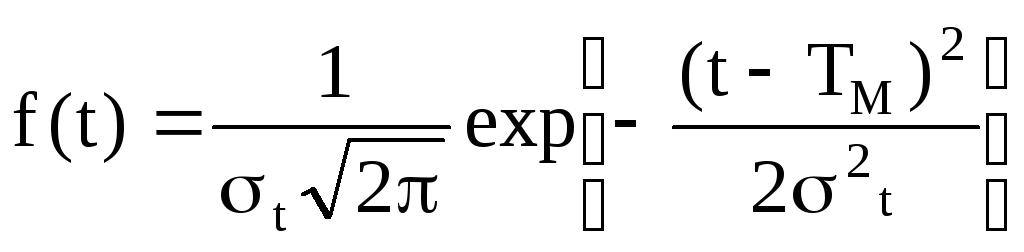- густина нормального розподілу;

С — нормуючий множник, який забезпечує нормування кривої розподілу, тобто 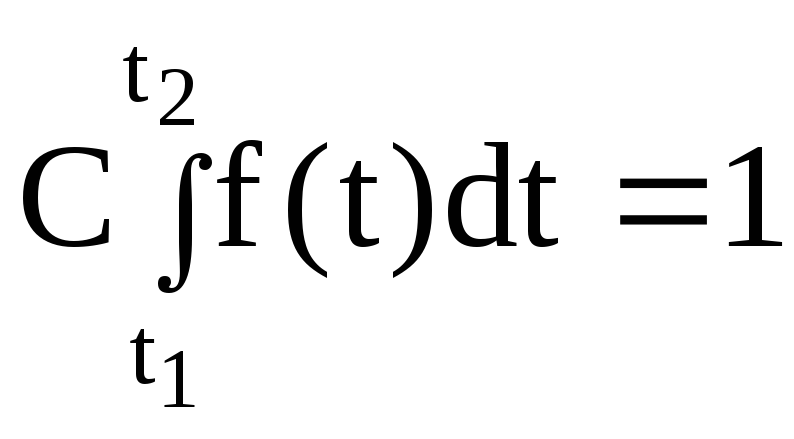, звідки

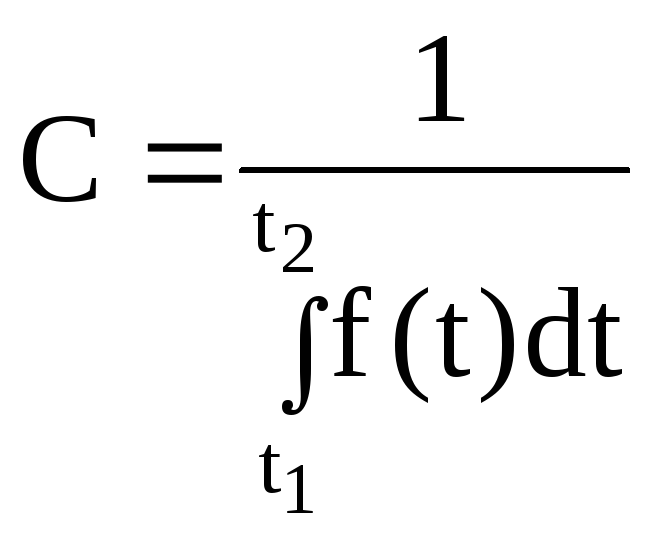(2.66)

Підставимо в (2.66) вираз для f(t) і, застосувавши позначення

,

де T_M- середній час наробки до відмови; — середнє квадратичне відхилення часу наробки до відмови для незрізаного розподілу, після перетворень отримаємо:

(2.67)

де — нормальна функція Лапласа.

Таблиця значень цієї функції наведена в додатку 2.

У випадку 0 < t <  (а саме цій умові відповідає зрізаний нормальний розподіл) отримаємо такі вирази для функцій:

а)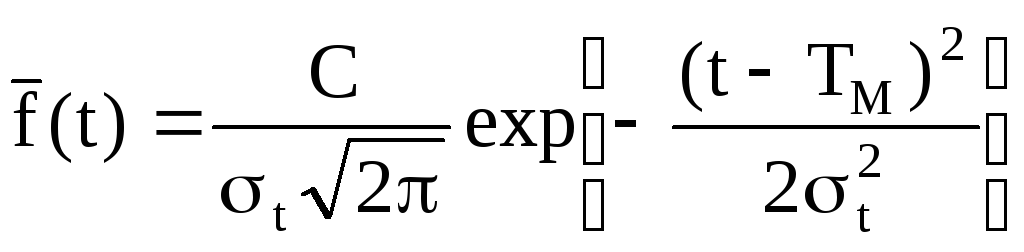 (2.66)

де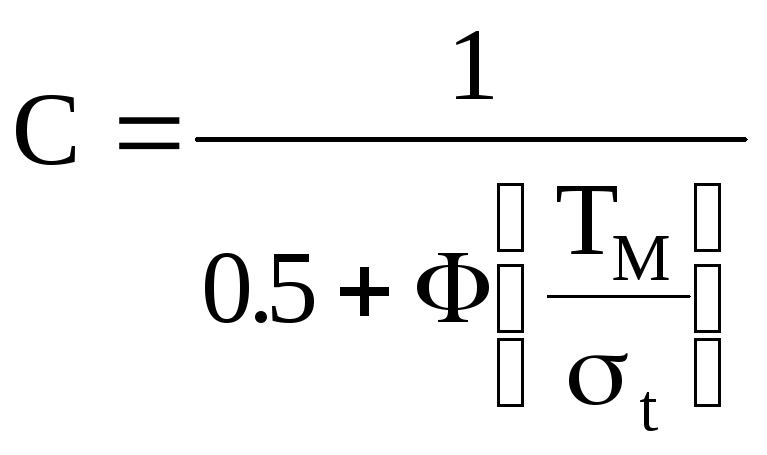

б) (2.69)

в) (2.70)

г) (2.71)

де

(2.72)

На рис. 2.9 наведені залежності відношення числових характеристик зрізаного і незрізаного нормального розподілу і значені нормуючого множника С від співвідношення Т_м /.

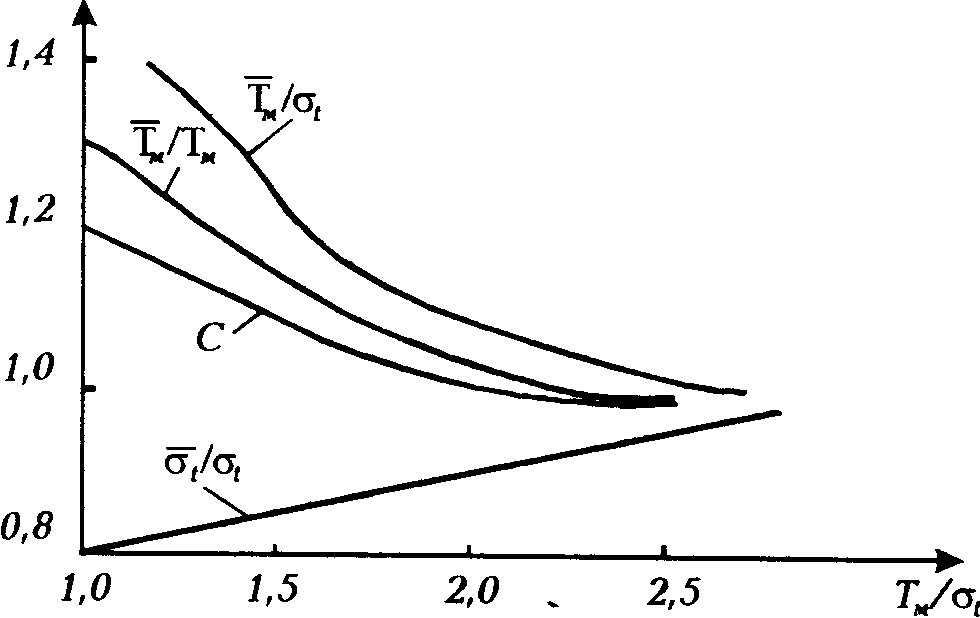
Рис.2.9. Залежність відношення числових характеристик

зрізаного і незрізаного нормального розподілу (риска над і означає, що ці характеристики належать до зрізаного розподілу).

Як видно з рис.2.9. при />2, що переважно спостерігається на практиці, значення С мало відрізняється від 1, а також  T_M, _t Тому досить часто слово «зрізаний» в назві розподілу опускають.

Графічне зображення f(t), (t), P(t) для зрізаного розподілу показано на рис.2.10.

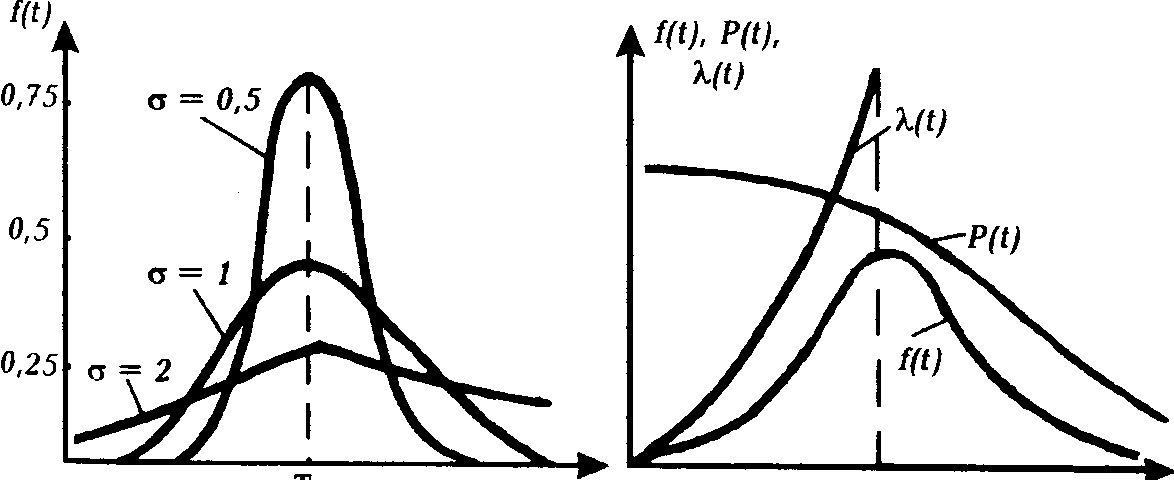
Рис.2.10. Функціональні залежності при нормальному законі розподілу.

Необхідно відзначити, що умовою нормального розподіл наробки до відмови є малий розкид значень швидкостей зношування елементів, тому що саме поява відмов за рахунок зношування елементів найкраще моделюється нормальним законом розподілу.

Бувають випадки явно несиметричних розподілів часу наробки до відмови. Тоді за модель f(t) беруть логарифмічний нормальний закон розподілу.

Логарифмічний нормальний (логнормальний) розподіл задається густиною розподіл

(2.73)

де  — середнє значення випадкової величини t;  — середньоквадратичне відхилення величини ln t.

Ймовірність безвідмовної роботи розраховують за такої формулою [14].

(2.74)

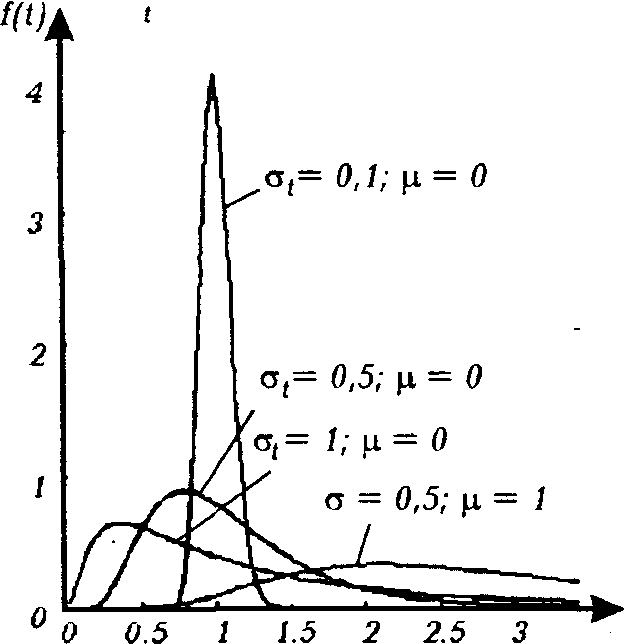
Рис.2.11. Криві густини при логарифмічному нормальному законі розподілу.

Криві густини логнормальног розподілу наведені на рис.2.11.

Дослідження, виконані в роботі [14] показують, що логнормальний закон розподілу часу відновлення (ремонту) характерний для випадків, коли системі керування електроприводами ремонтують, замінюючи несправні елементи, безпосередньо на міці де працює електропривод. Якщо у час відновлення входить такоз час пошуку несправностей і безпосередньо ремонт, то кращою математичною моделлю є окремий випадок — розподіл Ерланга другого порядку.

Розглянемо ще декілька законів розподілу, які можуть використовуватись для побудови математичних моделей надійності.

Розполіл Релея описують виразами [4];

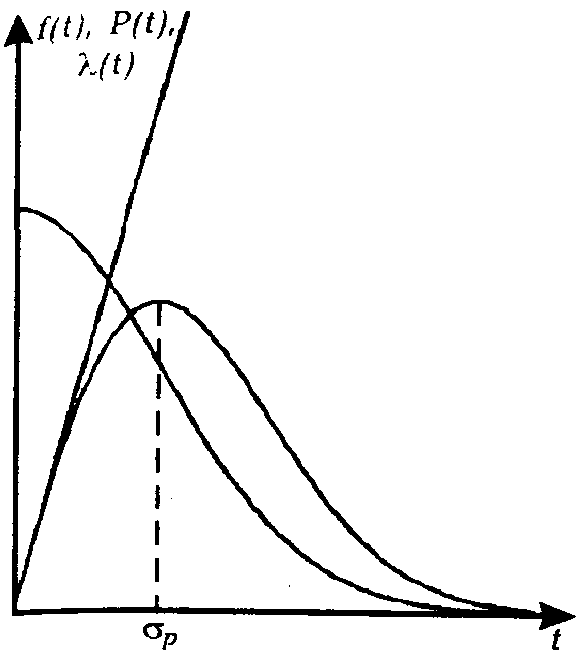
Рис.2.12. Графічні залежності розподілу Релея.

f(t)=t/²exp[-t²/(2p²)] (2.75)

(2.76)

(2.77)

де _р — параметр розподілу Релея, який є модою розподілу (значення t, яке відповідає екстремуму функції) і його не слід плутати зі середньоквадратичним відхиленням.

Для розподілу Релея математичне сподівання (середній час наробки до відмови)

(2.78)

а дисперсія

(2.79)

Графіки функцій розподілу Релея показані на рис.2.12.

Трикутний розподіл характеризує випадкові величини, які мають обмежену область можливих значень (t_n, t_k)

Цей розподіл (рис.2.13) описують такі три параметри: t_n, t_k — межі допустимих значень, t_m — мода.

Якщо позначити f(t_m )= h то з визначення площі трикутника отримаємо:

0.5h(t_n- t_k)=1 (2.80)

З виразу (2.80) отримаємо

h=2/( t_n- t_k) (2.81)

Puc.2.13. Графічні залежності при трикутному розподілі.

Тоді запишемо густину розподілу f(t) з урахуванням (2.81) 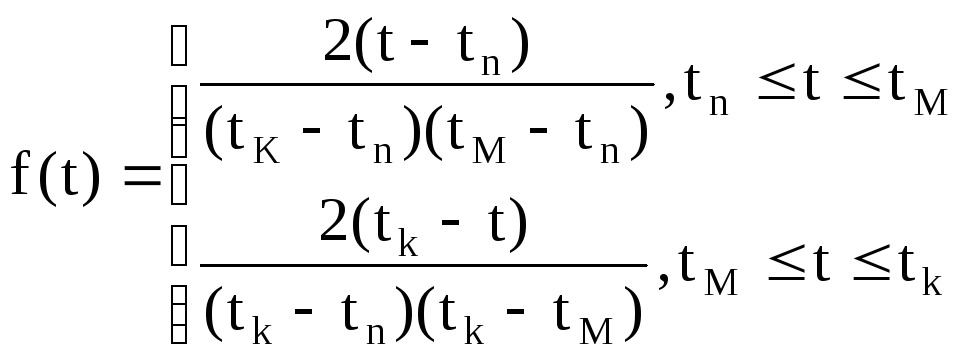(2.82)

Ймовірність безвідмовної роботи матиме вигляд:

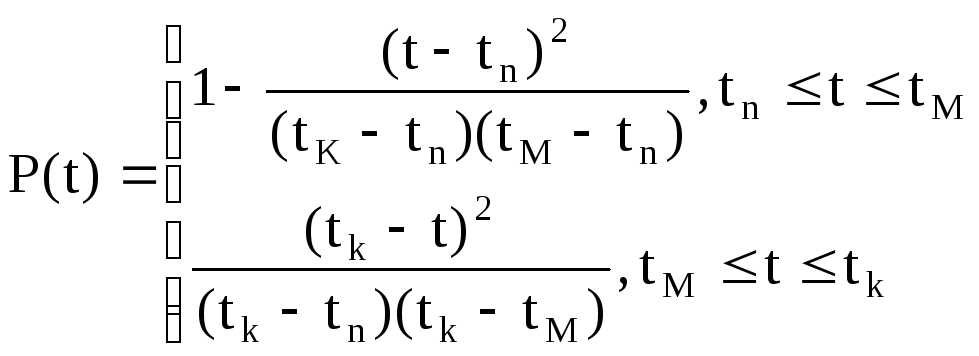(2.83)

Інтенсивність відмов для трикутного розподілу буде такою:

(2.84)

Біноміальний розподіл. Цей дискретний розподіл описує появу подій, які мають два значення, що взаємно виключають одне одного. Якщо, наприклад, в партії із 100 виробів 90 справних, а 10 бракованих, то ймовірність появи цих виробів становить 0,9 справних і 0,1 — бракованих. Очевидно, що коли в певну сукупність однакових виробів входять справні вироби, відносна частка яких становить р і браковані, відносна частка яких становить q, то p+q=l.

Якщо з великої партії однакових виробів з q % несправних, береться вибірка в кількості n, то ймовірності появи різної кількості несправних виробів в цих вибірках визначаються коефіцієнтами розкладання членів біноміального ряду

(Р + q)ⁿ =1

або

pⁿ+np^n-1q+n(n-1)p^n-2q²/2!+n(n-1)(n-2)p^n-3q³/3!+...+qⁿ=1 (2.85)

де q=q%/100% — частка одиниці несправних виробів в партії, а р — частка справних.

У рівнянні (2.85) рⁿ показує ймовірність відсутності несправних виробів у вибірці об'ємом n зразків, другий член np^n-1q дає ймовірність появи у вибірці одного несправного виробу, третій член — ймовірність появи у вибірці двох несправних виробів тощо, останній член qⁿ визначає ймовірність появи у вибірці n несправних елементів.

Приклад 2.1.

З великої партії сельсинів типу НС-404, в якій є q % =5% несправних зразків, береться для використання в системі вибірка з чотирьох машин (n=4). Визначити ймовірність появи у вибірках О, 1, 2, 3 чи 4 несправних сельсини.

Розв'язування.

; q =1-0.05 = 0.95. При цьому (p+q)⁴ = 1.

Тоді ймовірність появи у вибірці 0 несправних сельсинів:

p⁴=(0.95)⁴=0.8145.

Ймовірність появи у вибірці 1 несправного сельсина:

4p^зq=4(0,95)³0,05=0,1715.

Ймовірність появи у вибірці 2 несправних сельсинів:

6p²q²=6(0.95)²(0.05)²=0.0136.

Ймовірність появи у вибірці 3 несправних сельсинів:

4pq^з=4(0,95)(0,05)³=0,0004.

Ймовірність появи у вибірці 4 несправних сельсинів:

q⁴=(0,05)⁴=0,0000.

Повна ймовірність дорівнює 1,000.

Розподіл Пуассона. У випадку дискретного розподілу Пуассона розглядають події, ізольовані в часі чи просторі. Так, кількість відмов у роботі якоїсь системи протягом деякого проміжку часу характеризує появу ізольованих в часі подій.

Розподіл Пуассона, як і біноміальний, також складається з ряду членів, кожен з яких відповідно визначає ймовірність появи О, 1, 2, 3 чи більшої кількості подій на одиницю вимірювання. При цьому сума цих ймовірностей дорівнює одиниці. Розподіл Пуассона записують таким чином

(2.86)

де а- середня кількість несправних виробів, або несправностей на вибір при вибірці обємом n.

Величина а визначається як добуток обєму вибірки n на середнє значення частки кількості несправностей на вибір,або частки несправних виробів у цілій партії q,тобто ф=nq при цьому

або

У виразі (2.86) кожен член лівої частини означає:

e^-a - ймовірність появи 0 несправностей на виріб, або несправних виробів у вибірці;

ae^-a - ймовірність появи 1 несправності на вибір, або несправного виpобу у вибірці;

-ймовірність появи 2 несправностей на вибір, або двох несправних виробів у вибірці;

- ймовірність появи Ь несправностей на виріб, або b несправних виробів у вибірці.

Розподіл Пуассона зручно використовувати, наприклад, при контролі якості виробів. Він визначає основу для складання плану вибіркового прийому виробів у відділах технічного контролю підприємства.

Розподіл Пуассона при Ь = 0 і  =t перетворюється в експоненційний закон розподілу. Отже, експоненційний закон розподілу є окремим випадком закону розподілу Пуассона.