10.9. Моделирование рельефа

Рельеф может рассматриваться как атрибут информации наряду с другими атрибутами природного или социально-экономического характера.

Примерами таких атрибутов могут быть количественные и качественные характеристики почвы (кислотность, гранулометрический состав, гумусность и т.д.), состояние социально-экономической сферы (плотность населения, урожайность продукции, себестоимость, рентабельность производства и др.).

Для всех этих атрибутов можно применять одни и те же методы моделирования или один и тот же класс – группу моделей.

Различают модели, учитывающие структуру рельефа и не учитывающие.

Рассмотрим вначале модели, не учитывающие структуру рельефа. Их применяют в плоскоравнинных и пойменных районах.

В таких моделях значения атрибутов, в данном случае – высоты, располагаются в точках сети квадратов, треугольников и других равносторонних фигур.

К таким моделям можно отнести модель билинейного интерполирования. При этом в интерполяции принимают участие четыре точки (рис. 10.13).

Рис. 10.13.

В таком случае отметка точки вычисляется по формуле:

(10.1)

в которой шаг сетки, текущие приращения координат относительно левого нижнего угла квадрата, высоты вершин сетки квадратов.

Если принять то формула билинейной интерполяции превратится в формулу линейной:

(10.2)

А при

(10.3)

Из этого видно, что формула (10.1) выводится на основе (10.2) и (10.3) при величинах и не равных нулю.

Формулы (10.2) и (10.3) применены для интерполирования с четырех узловых точек. Если их применять для шестнадцати точек куба, то можно вывести формулу бикубической интерполяции.

Следующий метод основан на ортогональных полигонах Чебышева вида

(10.4)

где и соответственно номера ортогональных стандартных полигонов Чебышева и

Если принять максимально возможное значение для равным 2, и для равным 2, то формулу (10.4) можно записать так:

(10.5)

Если стандартные полигоны заданы, то значения коэффициентов следует найти. Их находят по методу наименьших квадратов на основе следующей минимизации

(10.6)

или с учетом (10.5)

(10.7)

Дифференцирование (10.7) по приводит к следующей системе уравнений:

(10.8)

Из решения которой находятся коэффициенты

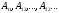
В том случае, когда решение состоит из треугольников (не обязательно равносторонних) используется интерполяция с помощью скользящей плоскости, которая строится по трем вершинам треугольников.

Пусть имеется треугольник (рис. 10.14) у которого известны координаты его трех вершин:

Рис. 10.14

Тогда принадлежность точки треугольнику 123 определится следующим равенством

(10.9)

Это условие того, что высоты являются линейными комбинациями X, Y, 1 т.е. справедливо равенство

.

Если обозначить

То уравнению (10.9) будет соответствовать следующее равенство:

Из которого следует, что

(10.10)

На основе (10.10) определяется отметка любой точки внутри треугольника.

Тип 2 интерполяции на основе триангуляции Делоне заключается в том, что высота определяемой точки вычисляется по формуле:

где:

(10.11)

а это ковариационный момент между отметкой определяемой точки и исходной с номером i, отметка этой исходной точки, ковариационный момент между исходными точками с номерами i и j.

Модели, учитывающие структуру рельефа, могут использовать элементы регулярных моделей.

К первому классу таких моделей относятся полиномы следующего вида

(10.12)

Частным случаем (10.12) является полный полином второй степени, который чаще всего используется на практике

(10.13)

коэффициенты которого определяются по методу наименьших квадратов при следующей минимизации

Во втором классе моделей по точкам, расположенным в характерных местах рельефа, строят поверхность, состоящую из суммы регулярных поверхностей вида

(10.14)

где

Для определения коэффициентов и решается система уравнений (10.14) для точек с известными высотами, число которых определяет размерность системы.