
- •Системы трёх линейных уравнений с тремя неизвестными имеют вид:
- •5, 6,7,8. Прямая на плоскости
- •9. Расстояние от данной точки до данной прямой
- •Угол между прямыми на плоскости
- •17.Векторное произведение векторов
- •18. Смешанное произведение трех векторов
- •Свойства предела последовательности. Общие свойства.
- •20. Предел функции
- •Свойства пределов функции
- •21. Непрерывность функции в точке.
- •2. Физический и геометрический смысл производной
- •1) Физический смысл производной.
- •2) Геометрический смысл производной.
- •Производные высших порядков
- •25. Ействия с комплексными числами, заданных в алгебраической форме
- •26. 1.4.3. Тригонометрическая форма записи комплексных чисел
- •28. Неопределенный интеграл
- •30. Интегрирование путем подведения под знак дифференциала
- •33. Формула Ньютона — Лейбница.
- •38. Функции нескольких переменных
- •39. I числовые ряды
- •40. Функциональные ряды
- •42. 1. Основные понятия
- •43. 2. Линейные дифференциальные уравнения первого порядка
- •45. Дифференциальные уравнения, допускающие понижение порядка
33. Формула Ньютона — Лейбница.
Сравнивая формулы площади криволинейной трапеции
![]() и
и ![]()
делаем вывод: если F — первообразная для f на [а; b] то
![]() (1)
(1)
33.Формула (1) называется формулой Ньютона — Лейбница. Она верна для любой функции f, непрерывной на отрезке [а; b
Сформулируем некоторые свойства определенного интеграла в предположении, что подынтегральная функция ограничена на отрезке, по которому она интегрируется.
-
Если функция интегрируема на [a; b], то она интегрируема на любом отрезке

-
Для любых a, b и c

-
Интеграл обладает свойством линейности: для любых функций f (x) и g (x) и любой постоянной A

-

-
Если f (x) и g (x) интегрируемы на [a; b], то f (x) · g (x) также интегрируема на этом отрезке.
-
Если f (x) – периодическая функция с периодом T, то для любого a
|
|
34.
Замена переменной в определённом
интеграле. Теорема.
Пусть функция ![]()
-
определена, непрерывно дифференцируема и монотонна на отрезке
 ,
, -
 ,
, -
функция
 непрерывна
на отрезке [a, b].
непрерывна
на отрезке [a, b].
Тогда  .
.
![]() Док-во.
Пусть F(x) -
первообразная для функции f(x),
т.е.
Док-во.
Пусть F(x) -
первообразная для функции f(x),
т.е. ![]() ,
тогда
,
тогда ![]() -
первообразная для функции
-
первообразная для функции ![]() .
.  ,
что и требовалось доказать.
,
что и требовалось доказать.
![]() При
решении задач нельзя забывать о том,
что при переходе к новой переменной
надо обязательно вычислить новые пределы
интеграла.
При
решении задач нельзя забывать о том,
что при переходе к новой переменной
надо обязательно вычислить новые пределы
интеграла.
![]() Пример:
Пример:

 .
.
35. Теорема 2. Если u(x) и v(x) - две функции, заданные на промежутке [a, b] и имеющие там непрерывные производные, то


![]() (24)
(24)
Формула (24) есть формула интегрирования по частям для определенных интегралов.
Доказательство очень просто. Именно,
![]()
![]()
Так как по формуле интегрирования по частям будет
![]()
![]()
![]()
то
![]()
![]()
![]()
откуда и следует (24).
Пример 1.
![]()
![]()
![]()
Здесь применена подстановка ln x = z (причем формула (22) прочитывалась слева направо).\
36
37
38. Функции нескольких переменных
Функции двух переменных Приращение функции
![]()
Функция,
дифференцируемая в точке ![]()
![]() при
при ![]()
В
этом случае дифференциал функции в
точке ![]() :
:
![]()
 -
частные производные, вычисленные в
точке
-
частные производные, вычисленные в
точке ![]() .
.
Дифференцирование композиции
1.
Если ![]() то
то
![]()
2.
Если ![]() то:
то:
![]()
![]()
![]()
Однородная функция степени k
![]()
39. I числовые ряды
Признак сравнения
1)
Если ![]() ,
начиная с некоторого
,
начиная с некоторого ![]() и
ряд
и
ряд  (2)
сходится, то ряд (1) также сходится, а
если ряд (1) расходится, то расходится и
ряд (2).
(2)
сходится, то ряд (1) также сходится, а
если ряд (1) расходится, то расходится и
ряд (2).
В качестве рядов для сравнения удобно рассматривать :
а)
геометрическую прогрессию  ,
, ![]() ,
сходящуюся при
,
сходящуюся при ![]() и
расходящуюся при
и
расходящуюся при ![]() ;
;
б)
гармонический ряд ![]() ,
который расходится;
,
который расходится;
в)
ряд Дирихле  ,
сходящийся при
,
сходящийся при ![]() и
расходящийся, при p<1 (
что доказывается с помощью интегрального
признака Коши).
и
расходящийся, при p<1 (
что доказывается с помощью интегрального
признака Коши).
2)
Если существует конечный и отличный от
нуля предел ![]()
![]()

![]() (в
частности,
(в
частности, ![]() ,
то ряды (1)
и (2) сходятся и расходятся одновременно.
,
то ряды (1)
и (2) сходятся и расходятся одновременно.
Пример
1. Исследовать на сходимость ряд  .
.
Так
как данный n-й
член ряда имеет вид ln(1+![]() ),
где
),
где ![]() -
бесконечно малая величина при n
-
бесконечно малая величина при n![]() ,
и известно, что ln(1
,
и известно, что ln(1![]()
![]() ,
то этот ряд сравниваем с рядом
,
то этот ряд сравниваем с рядом
 ,
представляющим собой бесконечно
убывающую геометрическую прогрессию
со знаменателем q=1/7<1,
которая сходится, следовательно, и
исходный ряд сходится.
,
представляющим собой бесконечно
убывающую геометрическую прогрессию
со знаменателем q=1/7<1,
которая сходится, следовательно, и
исходный ряд сходится.
Пример
2. Исследовать ряд 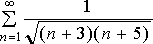 .
.
n-й
член данного ряда:  ~
~  ,
т.е. при n
,
т.е. при n![]() ведет
себя как гармонический, следовательно,
ряд также расходится.
ведет
себя как гармонический, следовательно,
ряд также расходится.
Часто,
прежде чем использовать какой-либо
из достаточных признаков сходимости
ряда, необходимо использовать понятие
эквивалентных бесконечно малых величин
при ![]() и
обязательно проверить необходимые
условия сходимости исследуемого ряда.
и
обязательно проверить необходимые
условия сходимости исследуемого ряда.

