17.Векторное произведение векторов

Векторным произведением вектора  на вектор  называется вектор, обозначаемый символом  и определяемый следующими тремя условиями:

1). Модуль вектора  равен , где  - угол между векторами  и ;

2). Вектор  перпендикулярен к каждому из вектора  и ;

3). Направление вектора  соответствует «правилу правой руки». Это означает, что если векторы ,  и  приведены к общему началу, то вектор  должен быть направлен так, как направлен средний палец правой руки, больой палец которой направлен по первому сомножителю (то есть по вектору ), а указательный - по второму (то есть по вектору ).

Векторное произведение зависит от порядка сомножителей, именно:

.

Модуль векторного произведения  равен площади S параллелограмма, построенного на векторах  и :

.

Само векторное произведение может быть выражено формулой

,

где  - орт векторного произведения.

Векторное произведение  обращается в нуль тогда и только тогда, когда векторы  и  коллинеарны. В частности, .

Если система координатных осей правая и векторы  и  заданы в этой системе своими координатами:

, ,

то векторное произведение вектора  на вектор  определяется формулой

,

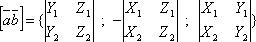или

18. Смешанное произведение трех векторов

Тройкой векторов называются три вектора, если указано, какой из них считается первым, какой вторым и какой третьим. Тройку векторов записывают в порядке нумерации; например, запись , ,  означает, что вектор  считается первым,  - вторым,  - третьим.

Тройка некомпланарных векторов , ,  называется правой, если составляющие ее векторы, будучи приведены к общему началу, располагаются в порядке нумерации аналогично тому, как расположены большой, указательный и средний пальцы правой руки. Если векторы , ,  расположены аналогично тому, как расположены большой, указательный и средний пальцы левой руки, то тройка этих векторов называется левой.

Смешанным произведенем трех векторов , ,  называется число, равное векторному произведению , умноженному скалярно на вектор , то есть .

Имеет место тождество, ввиду чего для обозначения смешанного произведения  употребляется более простой символ . Таким образом,

, .

Смешанное произведение  равно объему параллелепипеда, построенного на векторах , , , взятого со знаком плюс, если тройка  правая, и со знаком минус, если эта тройка левая. Если векторы , ,  компланарны (и только в этом случае), смешанное произведение  равно нулю; иначе говоря, равенство

есть необходимое и достаточное условие компланарности векторов , , .

Если векторы , ,  заданы своими координатами:

, , ,

то смешанное произведение  определяется формулой

.

Напомним, что система координатных осей предполагется правой (вместе с тем является правой и тройка векторов , , ).

19.

Последовательность, одно из основных понятий математики. П. образуется из элементов любой природы, занумерованных натуральными числами 1, 2,..., n,..., и записывается в виде x₁, x₂, …, x_n, … или коротко, {x_n}. Элементы, из которых составляется П., называются её членами. Члены П., стоящие на разных местах, могут совпадать. П. можно рассматривать как функцию от натурального аргумента (т. е. функцию, определённую на множестве натуральных чисел). Обычно П. определяется заданием n-го члена или рекуррентной формулой, по которой каждый следующий член определяется через предыдущий (см., например, Фибоначчи числа). Наиболее часто встречаются числовые и функциональные П. (т. е. П., членами которых являются числа или функции). Примеры:

1, 2, …, n, …, то есть x_n = n;     (1)

 , то есть  ;     (2)

 ,

то есть  ;     (3)

 ,

то есть  ;     (4)

Если элементы числовой П. при достаточно больших номерах n сколь угодно мало отличаются от числа а, то П. называется сходящейся, а число а — её пределом (аналогично определяется предел при функциональных П.). Например, П. (2) и (4) — сходящиеся, и их пределами служат число 0 и функция 1/(1 + x²). Несходящиеся П., например (1) и (3), называются расходящимися.

В математике пределом последовательности элементов пространства называют элемент того же пространства, который обладает свойством «притягивать», в некотором смысле, элементы данной последовательности. Свойство последовательности, иметь или не иметь предел, называют сходимостью: если у последовательности есть предел, то говорят, что данная последовательностьсходится, в противном случае (если у последовательности нет предела) говорят, что последовательность расходится. Часто встречающимся является предел числовой последовательности.