Вопрос № 19-(39) Производные сложной и обратной функции
Производная сложной функции
Рассмотрим сложную функцию y = y(u(x))
Теорема 4. Если функции y = y(u), u = u(x) дифференцируемы (т.е. существуют производные y'u, u'x), тогда сложная функция y = y(u(x)) дифференцируема и y'x = y'u u'x.
Доказательство
Если аргумент x получит приращение Δx, то функция u получит приращение Δu = u(x + Δx) − u(x), а функция y получит приращение Δy = y(u + Δu) − y(u). Но тогда, воспользовавшись свойствами предела функции, получаем
Теорема доказана.
Производная обратной функции
Рассмотрим функцию y = f(x), для которой существует обратная функция x = g(y).
Теорема
5.
Если обратная функция x
= g(y)
дифференцируема и g'(y)
≠
0,
то функция y=f(x)
дифференцируема, и
Доказательство
Если аргумент x получит приращение Δx, то функция f получит приращение Δy = f(x + Δx) − f(x). С другой стороны, для обратной функции g приращения Δx, Δy связаны следующим образом: Δx=g(y + Δy) − g(y).
Тогда получаем
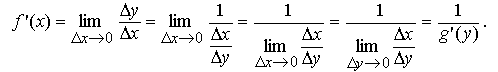
Теорема доказана.
Вопрос № 22-(42) Теорема Роля, Коши, Лангранжа о дифференцируемых функциях
Теорема Ролля. Если функция y= f(x) непрерывна на отрезке [a; b], дифференцируема во всех внутренних точках этого отрезка (т.е. на (а; b)) и на концах отрезка обращается в нуль f(a) = f(b) = 0, то на (a; b) найдется хотя бы одна точка c Î (a; b), в которой f'(c) = 0.
|
Теорема Лагранжа. Если функция y= f(x) непрерывна на [a; b] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [a; b] найдется хотя бы одна точка c, a<c<b такая, чтоf(b) – f(a)=f'(c)(b – a). |
|
Теорема
Коши.
Если f(x)
и g(x)
– две функции, непрерывные на [a;
b]
и дифференцируемые внутри него, причем
g'(x)
≠ 0 при всех x
Î (a;
b),
то внутри отрезка [a;
b]
найдется хотя бы одна точка c
Î (a;
b),
что
.
Билет № 17-(37) Правило дифференцирования. Таблица производных
Если с - постоянное число, и u = u(x), v = v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
1) (с) ' = 0, (cu) ' = cu';
2) (u+v)' = u'+v';
3) (uv)' = u'v+v'u;
4) (u/v)' = (u'v-v'u)/v2;
5)
если y = f(u), u = j(x), т.е. y = f(j(x)) -
сложная функция,
или суперпозиция,
составленная из дифференцируемых
функций j и f, то
,
или
;
6)
если для функции y = f(x) существует обратная
дифференцируемая функция x = g(y), причем
≠ 0, то
.
Таблица производных
Вопрос № 16-(36)
Уравнение касательной и нормали к графику функции
Пусть функция задается уравнением y=f(x), нужно написать уравнение касательной в точке x0 . Из определения производной: y/(x)=limΔx→0ΔyΔx Δy=f(x+Δx)−f(x). Уравнение касательной к графику функции: y=kx+b (k,b=const). Из геометрического смысла производной: f/(x0)=tgα=k Т.к. x0 и f(x0)∈ прямой, то уравнение касательной записывается в виде: y−f(x0)=f/(x0)(x−x0) , или y=f/(x0)·x+f(x0)−f/(x0)·x0.
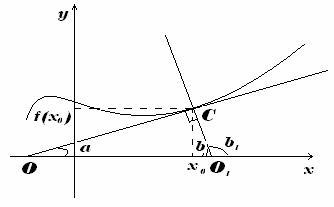
Уравнение нормали
Нормаль -- это перпендикуляр к касательной (см. рисунок). Исходя из этого: tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)
Т.к. угол наклона нормали -- это угол β1, то имеем: tgβ1=tg(π−β)=−tgβ=−1f/(x). Точка (x0,f(x0))∈ нормали, уравнение примет вид: y−f(x0)=−1f/(x0)(x−x0).