§2. Анализ функции f(e)

Выпишем функцию распределения Ферми-Дирака в следующем виде:

Нетрудно убедиться, что при E = E_F функция f(E) = 1/2.

Поведение функции f(E) (и электронного газа в металле) зависит от соотношения между температурой металла T и температурой Ферми (10.11).

При T << T_F (т.е. kT << E_F) электронный газ называют вырожденным и график функции f(E) незначительно отличается от ступени. В самом деле, показатель экспоненты (E - E_F) / kT будет велик по модулю всюду, за исключением интервала энергий, в котором (E - E_F) ≤ kT. При этом, если E < E_F, то (E - E_F) / kT будет величиной отрицательной и большой по модулю, значит экспонента будет близка к нулю, а f(E) ≈ 1. В случае, если E > E_F, показатель экспоненты будет большой положительной величиной и f(E) ≈ 0.

 Запишем результаты анализа в следующем виде:

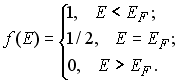
Из оценок, сделанных в § 2 лекция 10, T_F ≈ 60000K, значит вплоть до T_пл - температуры плавления металлов, электронный газ вырожден (самый тугоплавкий металл, вольфрам, имеет T_пл ≈ 3693K).

При T >> T_F электронный газ называется невырожденным. В этом случае график функции f(E) идет полого спадая и уже совсем не похож на ступеньку.

На рисунке 11.2 приведены графики функции f(E) (11.4) для различных температур.

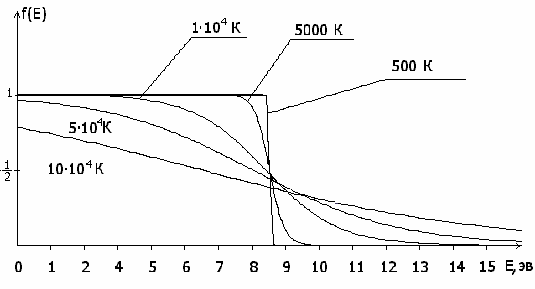
Рис. 11.2

При больших значениях энергии электронов, таких, что E - E_F >> kT, единицей в знаменателе функции f(E) (11.4) можно пренебречь, тогда для "хвоста" функции f(E) справедлива следующая формула:

что совпадает с распределением Максвелла-Больцмана (см. Ч. 3, (2.14)).

Итоги лекции n 11

1. Зависимость среднего числа фермионов в одном квантовом состоянии <n(E_i)> от их энергии и температуры называется распределением Ферми-Дирака (см. (11.1)):

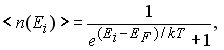
        здесь Е_F - уровень Ферми, параметр распределения, который определяют из условия нормировки. Другое название этого параметра - химический потенциал, который принято обозначать греческой буквой µ, т.е. E_F ≡ µ.

2. При не очень высоких температурах, когда kT<<E_F для уровня Ферми  справедливо приближенное выражение (см. (11.3)):

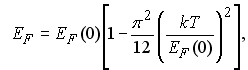
         здесь E_F(0) - энергия Ферми.

3. Так как среднее число фермионов в одном квантовом состоянии изменяется от 0 до 1, т.е. в тех же пределах, что и вероятность f(E_i) заполнения данных квантовых состояний, то для f(E_i) справедлива формула (11.1а), аналогичная формуле (11.1):

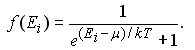
4. Анализ функции f(E) при Т=0 К дает следующие результаты:

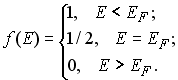
5. При больших значениях энергии электронов, таких, что Е-Е_F>>kT, для "хвоста" функции f(Е) справедлива формула (11.5):

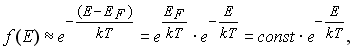
что совпадает с распределением Максвелла-Больцмана.

Лекция n 12 Результаты квантовой теории электропроводности. Термоэлектронная эмиссия. Бозоны. Распределение Бозе-Эйнштейна § 1. Результаты квантовой теории электропроводности металла

В Ч. 4 настоящего курса  была приведена  формула (6.9) для σ - удельной проводимости, полученная П. Друде в рамках классической теории электропроводности:

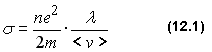
Из распределения Максвелла следует, что средняя скорость движения электрона в металле <v> пропорциональна корню квадратному из абсолютной температуры, т.е. . В результате из классической теории электропроводности следует, что , тогда как опыт дает   (см. Ч. 4, § 6).

Квантовая теория электропроводности дает для s следующую формулу:

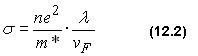
В этой формуле m* - эффективная масса электрона, которая учитывает влияние сил, действующих на электрон со стороны ионных остовов кристаллической решетки.

Скорость v_F с большой точностью можно считать независящей от температуры, таким образом температурная зависимость проводимости σ определяется зависимостью от температуры длины свободного пробега λ. Зависимость λ(T) обусловлена, в основном, тепловыми колебаниями атомов кристалла и при не очень низких температурах (T ≥ 100K) эта зависимость линейна, т.е. λ ~ T. Это и приводит к линейной зависимости удельного сопротивления от температуры, т.е.: