4.4. Синтез и анализ непараметрического решающего правила, основанного на оценках плотностей вероятности

Из байесовской решающей функции (4.1) соответствующей правилу максимума правдоподобия следует, что контрольная ситуация принадлежит тому классу, плотность вероятности распределения в котором наибольшая. Составим решающее правило, основанное на оценках плотностей вероятности.

Рассмотрим задачу распознавания образов на примере трёх классов наблюдений . Для восстановления плотностей вероятности воспользуемся непараметрической оценкой типа Розенблатта – Парзена

, (4.11)

где – количество ситуаций из обучающей выборки, принадлежащих -му классу.

В данном случае решающее правило имеет вид

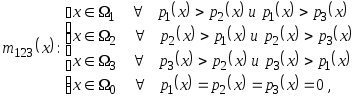(4.12)

где – неопределённый класс.

Разобьём обучающую выборку на три подвыборки

, (4.13)

, (4.14)

, (4.15)

где .

Используя данные подвыборки, запишем непараметрические оценки плотности вероятности для каждого из классов

,

,

,

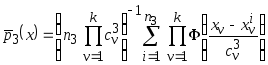– коэффициенты размытости ядерных функций оценок плотностей вероятностей распределения в классах . В данном случае задача оптимизации непараметрического решающего правила сводится к оцениванию параметров.

Когда – вектор, то каждому его признаку соответствует свой коэффициент размытости. Чем больше диапазон изменения признака, например,

тем больше значения принимает параметр размытости . Поэтому для упрощения задачи оптимизации многомерных непараметрических оценок плотностей вероятности (4.11) положим, что коэффициент размытости представим в виде произведения некоторого общего для всех признаков коэффициента и оценок их среднеквадратических отклонений . При этом коэффициенты размытости будут разные, но связующий их параметр будет общим ()

;

;

.

Оценки среднеквадратических отклонений для каждого признака в классах

, ,

, .

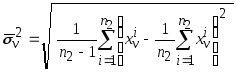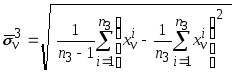Тогда непараметрические оценки плотности вероятности при синтезе решающего правила (4.12) примут вид

, (4.16)

, (4.17)

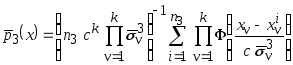. (4.18)

Задача оптимизации непараметрического решающего правила сводится к нахождению одного общего коэффициента размытости . При проведении вычислительных экспериментов установлено, что обычно диапазон изменения общего коэффициента размытости является постоянным .

Этапы оптимизации непараметрического решающего правила (4.12):

1. В качестве начального коэффициента размытости для плотностей (4.16–4.18) принять 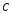=0.01. Ввести параметры .

2. Выбрать в качестве контрольной подвыборку (4.13), принадлежащую первому классу. Подставим последовательно элементы подвыборки (4.13) во все непараметрические оценки плотностей вероятности (4.16–4.18), учитывая в оценке (4.16) условие , т.е. исключается -я контрольная точка из восстановления оценки плотности . В данном случае оценки (4.16–4.18) принимают вид:

,

,

.

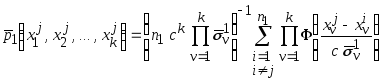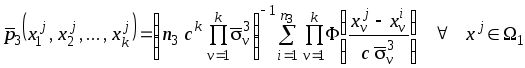Так как в качестве контрольной подвыборки используются наблюдения, принадлежащие первому классу, то оценка плотности должна быть больше, чем и . Если или , либо , то алгоритм распознавания образов принимает ошибочное решение. Данный факт фиксируется счётчиком .

В результате – количество точек первого класса, ошибочно отнесённых алгоритмом распознавания образов при конкретном коэффициенте размытости к другим классам.

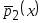3. Выбрать в качестве контрольной подвыборку (4.14) принадлежащую второму классу. Подставить элементы подвыборки (4.14) в непараметрические оценки плотностей вероятности (4.16–4.18), учитывая в оценке (4.17) условие , т.е. исключим -ю контрольную точку из обучения оценки плотности . В данном случае оценки (4.16–4.18) принимают вид:

,

,

.

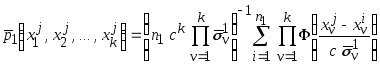Так как в качестве контрольной подвыборки используются наблюдения принадлежащие второму классу, то оценка плотности должна быть больше, чем и . Если окажется, что или , либо , тогда срабатывает счётчик ошибок .

В результате – количество точек второго класса, ошибочно отнесённых алгоритмом распознавания образов при конкретном коэффициенте размытости к другим классам.

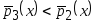4. По аналгии те же операции проведём и для элементов подвыборки третьего класса (4.15), подставляя их во все оценки плотностей вероятности (4.16–4.18), учитывая в оценке (4.18) условие . Если или , либо 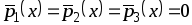, тогда срабатывает счётчик ошибок .

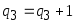В результате – количество точек третьего класса, ошибочно отнесённых алгоритмом распознавания образов при конкретном коэффициенте размытости к другим классам.

5. Рассчитать общее количество ошибочных решений 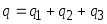во всех трёх классах. На этой основе оценить вероятность ошибки распознавания образов

при конкретном коэффициенте размытости .

6. Запомнить оценку вероятности ошибки и соответствующий коэффициент 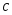. Увеличить текущее значение коэффициента размытост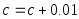и , если 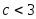тогда возвращаемся к этапу 2, иначе перейти к этапу 7.

7. Выбрать оптимальный коэффициент размытости , соответствующий минимальному значению оценки вероятности ошибки распознавания образов 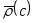(рис. 4.6)

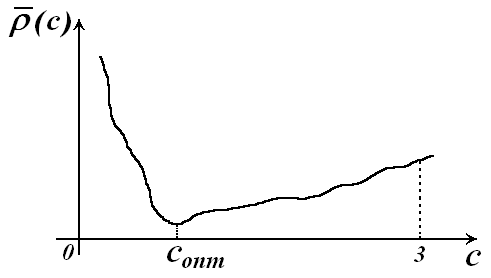
Рис. 4.6. Зависимость оценки вероятности ошибки распознавания образов от коэффициента размытости ядерной функции

Подставляя оптимальный коэффициент размытости в непараметрические оценки плотности вероятности (4.16–4.18) и используя решающее правило (4.12), можно принимать решение о принадлежности новых наблюдений к тому либо иному классу.

Синтез решающего правила с двумя градациями точности. В данном решающем правиле выходная переменная в отличие от правила (4.12) принимает не дискретных значений, а , где – количество классов. Идея данного подхода основывается на отождествлении поступившего нового наблюдения с одним из имеющихся классов, но в отличие от традиционного подхода (4.12) наблюдение может быть существенно похожим на точки множества и не существенно похожим , но всё же более похожим на , чем на другие.

Рассмотрим графическую интерпретацию данного случая для двух классов в одномерном случае (рис. 4.7).

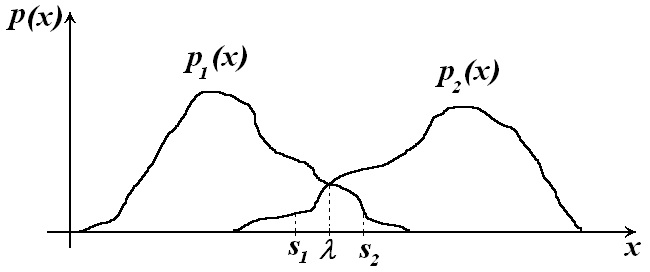
Рис. 4.7. Задача распознавания образов с двумя

градациями точности в одномерном случае

В данном случае решающее правило будет иметь вид

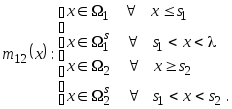
Для того чтобы учесть данную идею в решающем правиле (4.12) введём пороговую величину , которая характеризует степень отличия оценок плотностей вероятности. В результате решающее правило (4.12) принимает вид

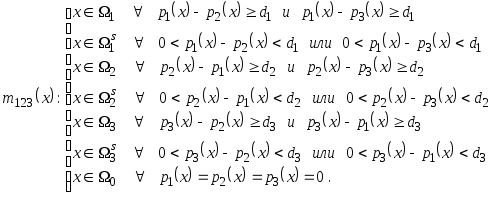
Пороговые значения, например, можно выбирать следующие:

, , .

По аналогии могут быть сформированы решающие правила с тремя и более градациями точности.