Глава 2. Прямые и плоскости

§1. Уравнение прямой на плоскости

1. Общее уравнение прямой

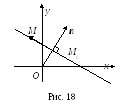Прямая на плоскости задается однозначно, если известен вектор, которому она перпендикулярна и точка, через которую она проходит. Вектор, перпендикулярный прямой, будем называть нормальным вектором, или вектором нормали, и обозначим через n(A, B), где (A, B) – координаты в прямоугольной декартовой системе координат. Точка, через которую проходит данная прямая, называется начальной точкой, обозначим ее M₀(x₀, y₀).

Произвольная точка М(x, y) лежит на прямой в том и только том случае, если вектор перпендикулярен вектору нормалиn (рис. 18). В свою очередь тогда и только тогда, когда скалярное произведение этих векторов равно нулю:

(n, ) = 0.

Учитывая, что вектор имеет координаты (x – x₀, y – y₀), запишем скалярное произведение:

A(x – x₀) + B(y – y₀) = 0.

Преобразуем это равенство

Ax + By – Ax₀ – By₀ = 0,

обозначим через C = – Ax₀ – By₀, получим

Ax + By + C = 0.

Это уравнение есть общее уравнение прямой. Напомним, что (А, В) – координаты нормального вектора.

Рассмотримчастные случаи.

1) А ≠ 0, B ≠ 0, C = 0 (т. е. вектор нормали n(A, B)), тогда уравнение примет вид

Ax + By = 0.

Эта прямая проходит через начало координат (0, 0).

2) А ≠ 0, B = 0, C ≠ 0 (т. е. вектор нормали n(A, 0)), тогда

Ax + C = 0 или .

Эта прямая параллельна оси Oy (рис. 19).

3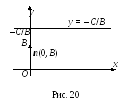)А = 0, B ≠ 0, C ≠ 0 (т. е. вектор нормали n(0, B)), тогда

By + C = 0 или .

Эта прямая параллельна оси Ox (рис. 20).

4) А ≠ 0, B = 0, C = 0 (т. е. вектор нормали n(A, 0)), тогда

Ax = 0 или x = 0.

Это уравнение оси Oy.

5) А = 0, B ≠ 0, C = 0 (т. е. вектор нормали n(0, B)), тогда

By = 0 или y = 0.

Это уравнение оси Ox.

2. уравнение прямой в отрезках

Пусть задано общее уравнение прямой

Ax + By + C = 0

и C ≠ 0, т.е. прямая не проходит через начало координат. Преобразуем уравнение следующим образом:

Ax + By = – C,

разделим уравнение на (– С), получим

,

перепишем дроби в виде:

;

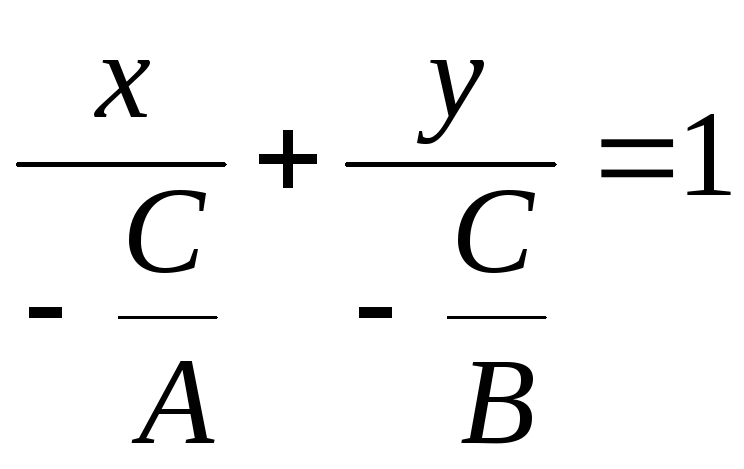обозначим и, получим

.

Это уравнение называется уравнением прямой в отрезках.

Установим смысл входящих в уравнение параметров, для этого дадим переменной х значение a, получим

=> =>y = 0.

Значит, прямая проходит через точку с координатами (a, 0).

Пусть теперь y = b, уравнение примет вид

=> =>x = 0.

Следовательно, прямая проходит через точку (0, b). Полученные точки (a, 0) и (0, b) представляют собой точки пересечения прямой с осями координат. Заметим, что параметры a и b могут быть как положительны, так и отрицательны, независимо друг от друга. Геометрический смысл их заключается в cледующем: a – это отрезок, который прямая отсекает по оси Ox от начала координат, a > 0, если отрезок отсекается в положительной части оси и a < 0 в другом случае; b – это отрезок, который прямая отсекает по оси Oy (рис. 21).

3. векторно-параметрическое и параметрические уравнения

прямой на плоскости

Прямая может быть задана однозначно не только с помощью нормального вектора, т. е. вектора, ей перпендикулярного. Прямая на плоскости задана однозначно, если известен вектор, параллельный прямой и начальная точка. Вектор, параллельный прямой, называется направляющим вектором прямой и обозначается q(q₁, q₂).

Произвольная точка М(x, y) лежит на прямой только в том случае, если вектор коллинеарен векторуq, и, следовательно, найдется такое число t, что будет выполняться равенство

= tq.

Обозначим через r(x, y) – радиус-вектор точки М(x, y), через r₀(x₀, y₀) – радиус-вектор точки М₀(x₀, y₀), тогда =r – r₀ и получаем

r – r₀ = tq.

Это векторно-параметрическое уравнение прямой. В полученном уравнении участвуют вектора: q – направляющий вектор, r₀ – радиус-вектор начальной точки, r – радиус-вектор произвольной точки прямой и параметр t. Запишем это уравнение через координаты соответствующих векторов:

r – r₀ = (x – x₀, y – y₀), tq = (q₁t, q₂t),

следовательно,

(x – x₀, y – y₀) = (q₁t, q₂t).

Приравняем соответствующие координаты:

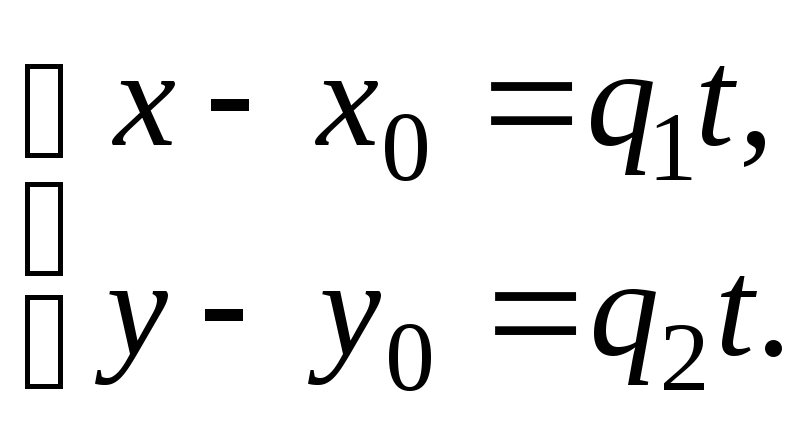
Получили параметрические уравнения прямой на плоскости, где (q₁, q₂) – координаты направляющего вектора, (x₀, y₀) – координаты начальной точки. Иногда эти уравнения записывают в виде

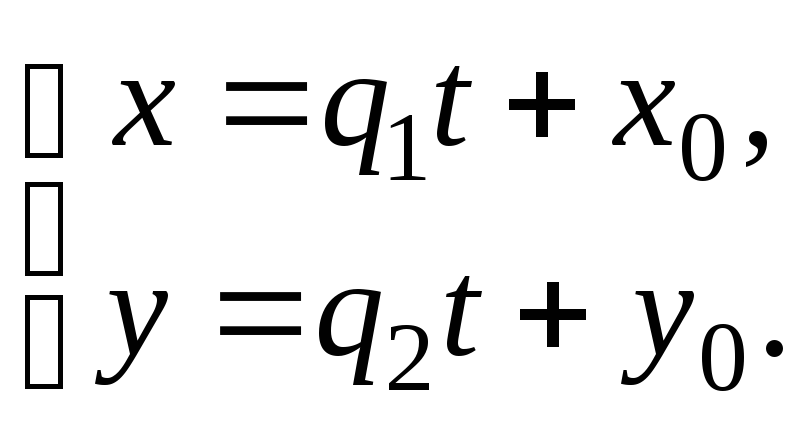
Рассмотримчастные случаи.

1) Пусть q₁ = 0, q₂ ≠ 0 (рис. 23), тогда

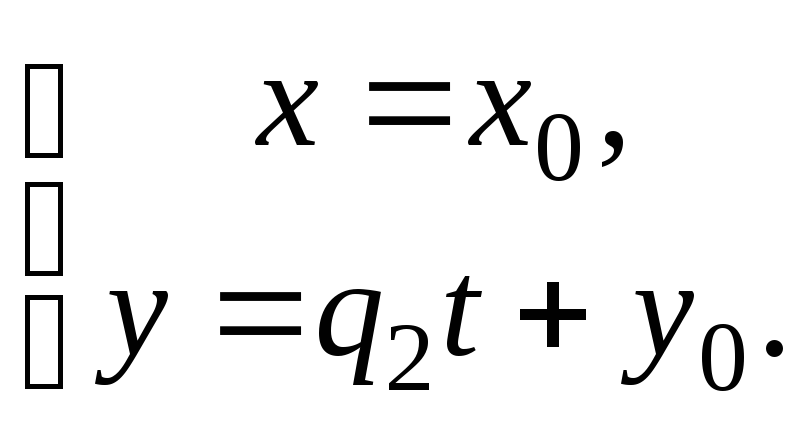
Учитывая, что t – произвольное число, то у принимает любые значения независимо от х, и прямая задается уравнениями:

2) Пусть q₁ ≠ 0, q₂ = 0 (рис. 24), тогда уравнения принимают вид

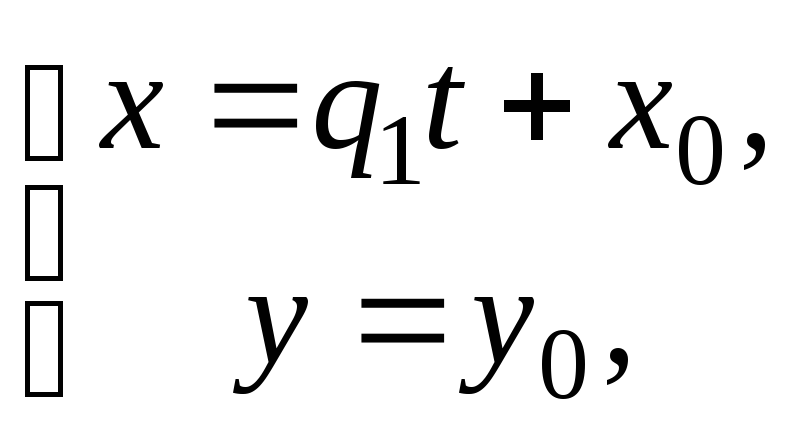
и, значит, х – любое и y = y₀.

4. каноническое уравнение прямой на плоскости

Пусть прямая задана своим направляющим вектором q(q₁, q₂) и начальной точкой М₀(x₀, y₀), предположим, что q₁ ≠ 0, q₂ ≠ 0. Из параметрических уравнений прямой вытекает

и ,