4.2. Непараметрические оценки решающих функций

Для получения непараметрической оценки разделяющей поверхности подставим в исходные байесовские функции (4.1), (4.2) непараметрические оценки плотности вероятности (например, оценку Розенблатта-Парзена для одномерного случая)

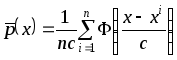. (4.3)

1. Получение непараметрической оценки разделяющей поверхности, которая соответствует правилу максимума правдоподобия

.

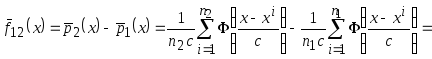
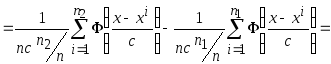
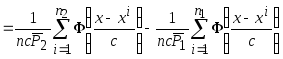В итоге получим

,

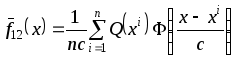где

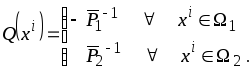
2. Получение непараметрической оценки разделяющей поверхности, которая соответствует правилу максимума апостериорной вероятности

.

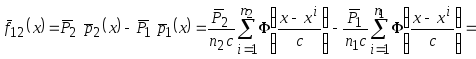
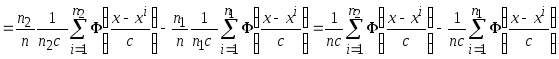В результате имеем

,

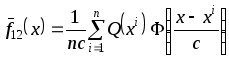где

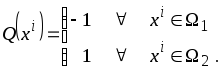
Для многомерного случая непараметрическая оценка разделяющей поверхности имеет вид

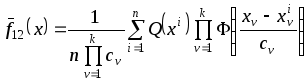. (4.4)

Оптимизация непараметрической оценки разделяющей поверхности по коэффициенту размытости. Нетрудно заметить, что непараметрические оценки решающей функции зависят от коэффициента размытости ядерной функции .

В данном случае оптимизация непараметрической оценки разделяющей поверхности проводится исходя из минимума ошибки распознавания

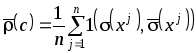, (4.5)

где – «указания учителя» из обучающей выборки;

– решения, полученные в соответствии с алгоритмом распознавания образов;

.

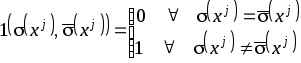Решения находятся с использованием решающего правила

,

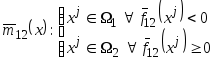где

.

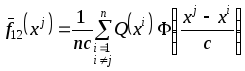Многоальтернативные задачи распознавания образов. Метод дихотомии – это метод сведения многоальтернативной задачи к последовательности двухальтернативных задач.

Рассмотрим метод дихотомии для трёх классов.

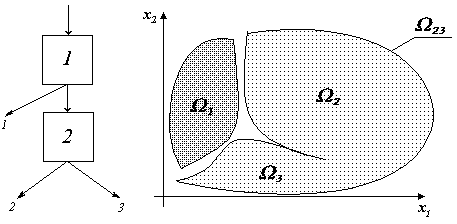
Рис. 4.5. Графическая иллюстрация метода дихотомии

Этапы формирования алгоритма:

1. На первом этапе разбиваем трёхальтернативную задачу на последовательность двухальтернативных, т.е. строим уравнение разделяющей поверхности между 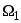и :

,

,

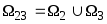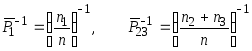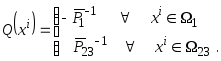
Тогда решающее правило имеет вид:

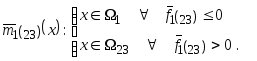
2. На втором этапе строим решающее правило классификации ситуаций классов 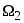и .

,

,

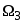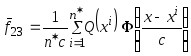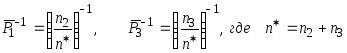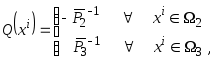
В соответствии с блок-схемой (рис. 4.5) получаемая система классификации функционирует следующим образом:

• Сигнал подаётся в первый алгоритм обработки информации . Если он принадлежит первому классу 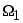, то решение принято.

• Если сигнал в соответствии с правилом 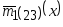принадлежит классу 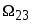, то процесс распознавания переходит к алгоритму .

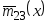4.3. Непараметрические алгоритмы распознавания образов коллективного типа

Структуру рассматриваемого класса алгоритмов распознавания образов составляют множество упрощенных параметрических аппроксимаций решающей функции, каждая из которых строится относительно некоторой «опорной» ситуации из обучающей выборки. Объединение упрощенных аппроксимаций в коллектив решающих функций реализуется с помощью непараметрической оценки оператора условного математического ожидания относительно «опорной» ситуации. При формировании решения участвуют упрощенные аппроксимации решающих функций с весами, определяемыми ядерной мерой близости между контрольной и «опорными» ситуациями.

Пусть обучающая выборка, составленная из параметров складывающейся ситуации и соответствующих им «указаний учителя» о принадлежности -й ситуации к одному, например, из двух классов.

Выберем из исходной обучающей выборки множество «опорных» точек и построим для каждой упрощённое (например, линейное) уравнение разделяющей поверхности между классами (опорная решающая функция).

Полученные функции , являются знакопеременными. Поэтому решающее правило, построенное на их основе, имеет вид

(4.6)

Параметры -й опорной решающей функции находятся из условия минимума оценки ошибки распознавания образов

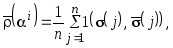(4.7)

где

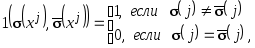
«Решение» о принадлежности ситуации к тому или иному классу определяется в соответствии с решающим правилом (4.6), которое сопоставляется с «указаниями учителя» из обучающей выборки .

Процесс отыскания параметров разделяющей поверхности должен осуществляться с учётом её прохождения через -ю опорную точку. Тогда общая постановка задачи идентификации -й решающей функции запишется в виде

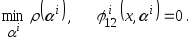(4.8)

Решение задачи (4.8) можно получить с помощью традиционных алгоритмов случайного поиска, например, метода наилучшей пробы.

Без существенного снижения эффективности строящегося коллектива решающих правил, вид уравнений разделяющих поверхностей может быть принят линейным, что значительно сократит требуемые вычислительные ресурсы.

С этих позиций непараметрический алгоритм распознавания образов коллективного типа в двуальтернативной задаче запишется как

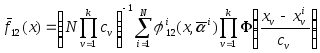. (4.9)

Отличие (4.9) от традиционной непараметрической байесовой оценки разделяющей поверхности (4.4) заключается в замене «указаний учителя»

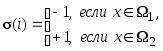
на упрощенные решающие функции .

Обобщенное решающее правило классификации формируется с учетом знака уравнения

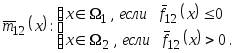
Для многоальтернативной задачи распознавания образов рекомендуется использовать метод дихотомии (см. пункт 4.2).

Для уменьшения вероятности ошибки и количества упрощённых параметрических уравнений разделяющей поверхности опорные точки необходимо выбирать из области пересечения классов. Дополнительно эффективность непараметрических коллективов классификации можно повысить за счёт использования результатов формирования их структуры. Для этой цели введём оценки показателя эффективности упрощённых параметрических решающих функций . В качестве показателя эффективности -го упрощённого уравнения может выступать оценка вероятности ошибки классификации , .

Тогда непараметрическое уравнение разделяющей поверхности с учётом эффективности упрощённых параметрических решающих функций примет вид

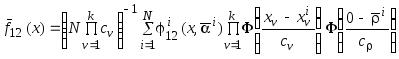. (4.10)

Применение данной модификации повышает помехозащищённость непараметрических коллективов и точность решения задачи классификации.