
- •Линейные волны
- •Волновое уравнение. Бегущие волны
- •Преобразование Фурье.
- •Монохроматическая волна.
- •Характеристики линейных волн.
- •Фазовая скорость линейных волн
- •Дисперсия среды. Групповая скорость линейных волн
- •Явление опрокидывания (укручения) нелинейных волн
- •Преобразование Коула – Хопфа. Ударные волны
- •Асимптотические решения уравнения Бюргерса. Ширина фронта ударной волны
- •Оценки ширины фронта ударной волны. Число Рейнольдса
- •Спектр ударной волны.
- •Солитоны
- •Стационарные волны
- •Солитонные решения волнового уравнения (общие свойства)
- •Солитонное решение уравнения Кортевега - де -Вриза
- •Решение уравнения КдВ (общий вид)
- •Законы сохранения
- •Нелинейные уравнения, обладающие солитонными решениями
- •Нелинейные уравнения, не имеющие решений в виде солитонов.
- •Динамический хаос
- •Нелинейный маятник
- •Характеристики нелинейного маятника.
- •Особенности движения вблизи сепаратрисы
- •Переменные: «Действие» и «угол»
- •Уравнение нелинейного маятника при наличии внешней периодической силы.
- •Перекрытие резонансов. Критерий стохастичности
- •Параметрический резонанс
-
Уравнение нелинейного маятника при наличии внешней периодической силы.
Рассмотрим маятник,
на который действует некоторая возмущающая
сила, т.е. потенциал
![]() ,
,
![]() - малый параметр
- малый параметр
Уравнение имеет вид:
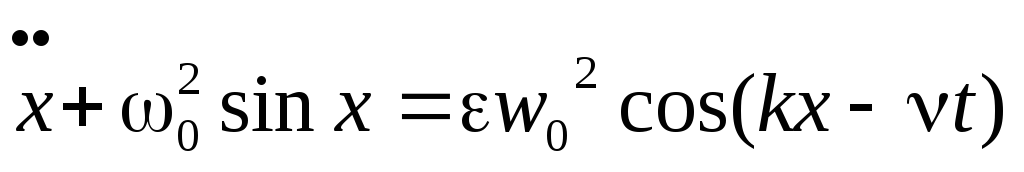 ,
,
Аналитически можно показать, когда в этом случае будет хаос
При малых амплитудах
колебания мятник можно считать линейным
![]() .
.
В этом случае спектр
невозмущенного маятника состоит из
одной гармоники с частотой
![]() .
В общем случае из-за нелинейности частота
зависит от энергии маятника, соответственно
период тоже зависит от энергии, при
стремлении, движение частицы, приближается
к сепаратрисе, частота с ростом энергии
уменьшается.
.
В общем случае из-за нелинейности частота
зависит от энергии маятника, соответственно
период тоже зависит от энергии, при
стремлении, движение частицы, приближается
к сепаратрисе, частота с ростом энергии
уменьшается.
Если правая часть не
равна 0, то накладывается еще волна
E2,при
этом
![]()
Будем рассматривать движение вблизи сепаратрисы.
Тогда полная энергия
системы
![]()
Где
![]()
Энергия частиц
![]() .
Изменение энергии частиц
.
Изменение энергии частиц
![]() .
.
Запишем изменение энергии как работу в 1 секунду:
![]()
Вблизи сепарастрисы:
![]()
При приближении энергии
маятника к сепаратрисе, частота стремиться
к 0, а Т>>![]() ,
где
,
где
![]() -
период колебания линейного маятника.
-
период колебания линейного маятника.
Тогда
![]() ,
так как
,
так как
![]() .
.
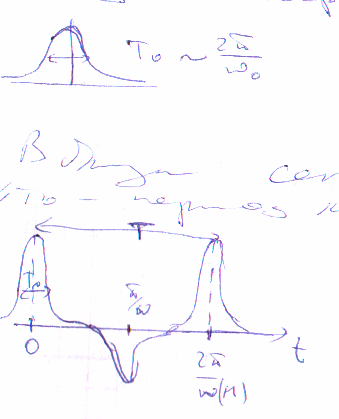

В результате такого движения частица очень бытро проходит почти всю область пространства и надолго застревает в Седловых точках сепарастрисы.
Такое движение можно рассматривать как движение под действием мгновенных толчков.
Тогда гамильтониан можно записать:
![]() ,
где V(x)-
некоторая функция.
,
где V(x)-
некоторая функция.
Перейдем к новым
переменным:
![]()
![]()
 - частота нелинейных
колебаний
- частота нелинейных
колебаний
=>
![]()
Т.к.
![]() ,
,
![]()
Тогда
![]()
=> Появилась периодическая составляющая.Это значит появилась возможность попадания в резонанс.
-
Перекрытие резонансов. Критерий стохастичности
Все возможные резонансы в системе определяются:
![]() ,
где m=1,2,3..
,
где m=1,2,3..
В окрестности
каждого резонанса можно построить
фазовые траектории, при этом резонансным
значения «действия» обозначается ![]()
Можно ввести фазу
вблизи резонанса как:
![]()

Построим фазовые траектории для каждого резонанса.
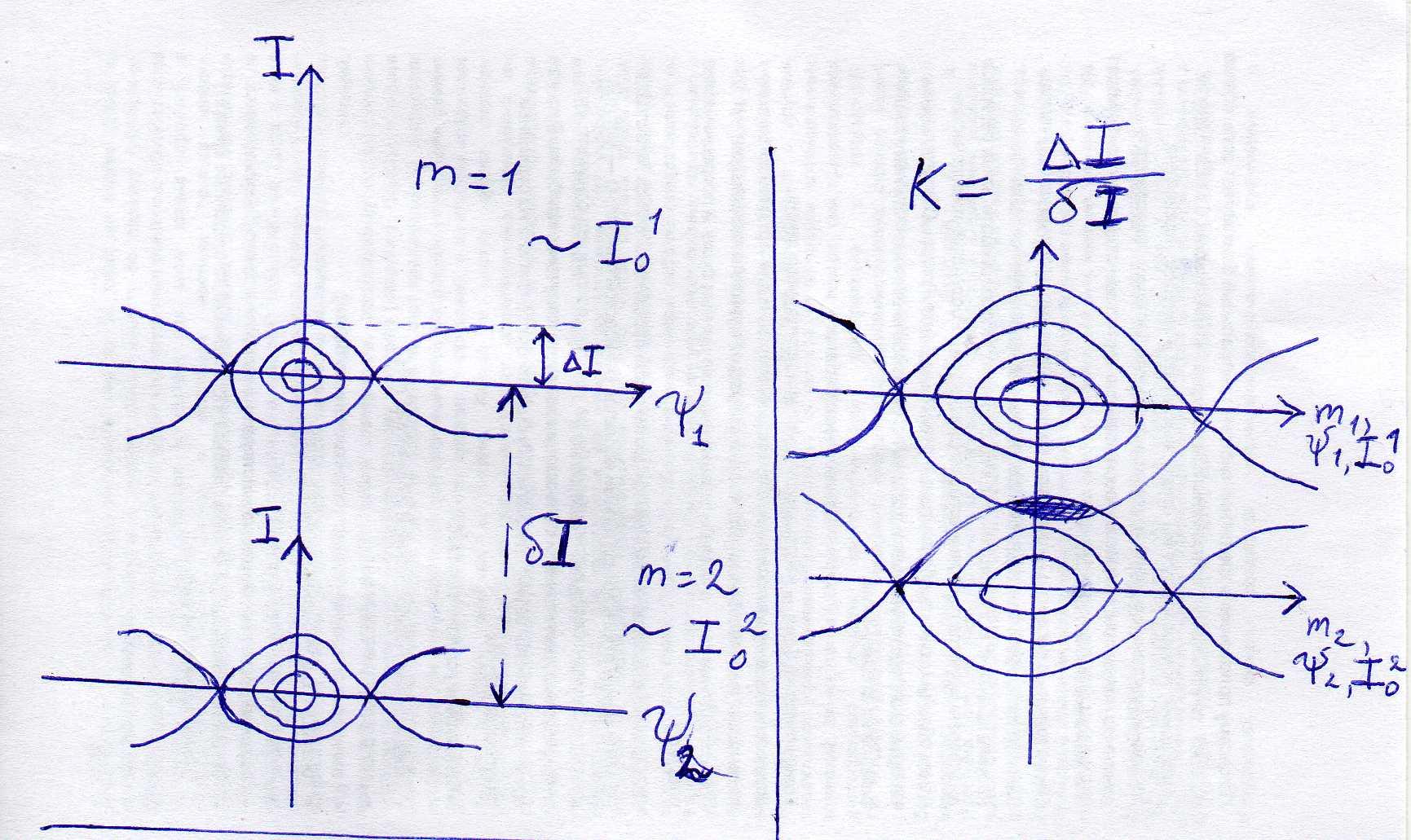
Введем параметр
![]()
Если k>>1, тогда частица может одновременно находится в более 2х резонансах. Резонансы перекрываются, это приводит к стохастическому поведению.
=> регулярные траектории исчезают и происходит разрушение сеператрисы.
Параметр нелинейности,
ширину сепаратрисы ![]() можно
определить, если рассмотреть отдельные
нелинейные резонансы
можно
определить, если рассмотреть отдельные
нелинейные резонансы
![]()
![]()
![]() //в точке резонанса
//в точке резонанса
Параметрический резонанс
Параметрический резонанс - возбуждение колебаний, наступающее в колебательной системе в результате периодических изменения величины какого-либо из энергоёмких параметров системы (т. е. параметров, от величины которых существенно зависят значения потенциальной и кинетической энергий и периоды собственных колебаний системы). Параметрический резонанс может происходить в любой колебательной системе, как в механической, так и в электрической, например при периодическом изменении длины математического маятника.
Параметрический резонанс наступает в случаях, когда отношение угловой частоты w0 одного из собственных колебаний системы к угловой частоте w изменений параметра (w0 / w) оказывается близким к n/2, где n = 1,2,3,...; тогда в системе могут возбудиться колебания с частотой, близкой к w0 и точно равной w/2, либо w, либо 3w/2 и т.д. Параметрический резонанс наступает легче всего, а возникшие колебания оказываются наиболее интенсивными, когда w0 / w = 1/2.
Классический пример параметрического резонанса в механической системе с распределенными параметрами - возбуждение интенсивных поперечных колебаний в струне, прикрепленной одним концом к ножке камертона (рисунок 1) путём периодического изменения её натяжения. Легче всего параметрический резонанс возникает, когда один из периодов собственных колебаний струны (её основного тона или какого-либо из гармоник) приблизительно вдвое больше периода колебаний камертона. При обычном же возбуждении вынужденных колебаний струны с периодом, равным периоду колебаний камертона, резонанс наступил бы всякий раз, когда период колебаний камертона совпадал бы с периодом одного из собственных колебаний струны. Таким образом, явление параметрического резонанса в этом отношении сходно с силовым резонансом при возбуждении вынужденных колебаний.
Параметрический резонанс от силового резонанса отличается формой резонансной кривой – в случае параметрического возбуждения колебаний резонанс наблюдается в строго ограниченной полосе частот (которая определяется значением n и амплитудой изменения параметра), в то время как при силовом воздействии на систему можно добиться существования колебаний на любой частоте.
П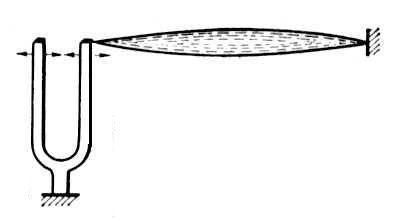 араметрическое
возбуждение колебаний струны:
араметрическое
возбуждение колебаний струны:
Параметрами
одномерного осциллятора, движущегося
с трением, являются его масса m,
коэффициент упругости k и
коэффициент затухания β.
Если эти коэффициенты зависят от времени,
и m = m(t),k = k(t),β
= β(t),
то уравнение движения имеет вид
![]()
Сделаем
замену переменной времени t →τ,
где dτ
= dt / m(t),
что приводит уравнение (1) к виду
![]()
Сделаем
еще одну замену x(τ) → q(τ):
![]()
Это позволит избавиться от члена, связанного с затуханием:
![]()
Поэтому
фактически, без всякого ограничения
общности, вместо уравнения (1) достаточно
рассмотреть уравнение движения вида
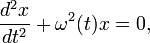 которое получилось бы из уравнения (1)
при m = const.
которое получилось бы из уравнения (1)
при m = const.
Интересно,
что в отличие от случая постоянной
частоты
![]() ,
аналитическое решение уравнения (5) в
общем виде неизвестно. В случае
периодической зависимости ω(t) уравнение
(5) является частным случаем уравнения
Хилла, а в случае гармонической
зависимостиω(t) —
частным случаем уравнения
Матье.
Наиболее
хорошо уравнение (5) изучено в случае,
когда частота колебаний гармонически
изменяется относительно некоторого
постоянного значения.
,
аналитическое решение уравнения (5) в
общем виде неизвестно. В случае
периодической зависимости ω(t) уравнение
(5) является частным случаем уравнения
Хилла, а в случае гармонической
зависимостиω(t) —
частным случаем уравнения
Матье.
Наиболее
хорошо уравнение (5) изучено в случае,
когда частота колебаний гармонически
изменяется относительно некоторого
постоянного значения.
-
Рассмотрим случай, когда
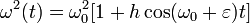 ,
то есть уравнение (5) имеет вид
,
то есть уравнение (5) имеет вид

Где ω0 —
частота собственных гармонических
колебаний, амплитуда гармонических
вариаций частоты
![]() ,
постоянная
,
постоянная
![]() — небольшая вариация частоты. Надлежащим
изменением начала отсчета времени
постоянную h можно выбрать положительной,
поэтому, не ограничивая общности, будем
считать, что h >
0.
Вместо решения уравнения (6) поставим
более скромный вопрос: при каких значения
параметра ε,
происходит резкое возрастание амплитуды
колебаний, то есть решение x(t) неограниченно
возрастает? Можно показать [1], что это
происходит в том случае, когда
— небольшая вариация частоты. Надлежащим
изменением начала отсчета времени
постоянную h можно выбрать положительной,
поэтому, не ограничивая общности, будем
считать, что h >
0.
Вместо решения уравнения (6) поставим
более скромный вопрос: при каких значения
параметра ε,
происходит резкое возрастание амплитуды
колебаний, то есть решение x(t) неограниченно
возрастает? Можно показать [1], что это
происходит в том случае, когда
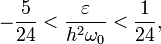
2. Рассмотрим
случай, когда
![]() ,
то есть уравнение (5) имеет вид
,
то есть уравнение (5) имеет вид
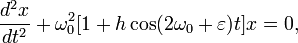
Иными
словами, гармоническое изменение
свободных колебаний происходит с
частотой y =
2ω0tε.
В этом случае параметрический резонанс,
с точностью до членов h2,
происходит в случае, когда
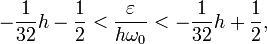
В частности,
укажем условия параметрического
резонанса для малых колебаний
математического маятника с колеблющейся
в вертикальном положении точкой подвеса,
для которого уравнения колебаний имеют
вид
![]()
Где
![]() ,
и
,
и ![]() .
В случае, когда
.
В случае, когда
![]() и
ограничиваясь первым порядком разложения
по h,
получим, что
и
ограничиваясь первым порядком разложения
по h,
получим, что
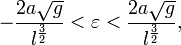
Тот факт,
что параметрический резонанс происходит
в окрестности частоты свободных
колебаний ω
= ω0 и
её удвоенного значения ω
= 2ω0, —
не случаен. Можно показать (см. напр.
[2]), что в случае уравнения
![]()
Параметрический
резонанс имеет место, когда
![]()
Главный
резонанс происходит при удвоенной
частоте собственных колебаний
гармонического маятника ω0,
а ширина резонанса равна hω0.
Важно также, что при наличии трения (см.
ур-е (2)), в уравнении
![]()
Имеет место
явление параметрического резонанса не
при любых
![]() , а лишь при тех
, а лишь при тех
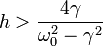 . Т.о., при наличии трения
. Т.о., при наличии трения
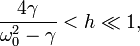
что позволяет надлежащим выводом параметров γ,ω0, и h, в зависимости от практической необходимости, усилить или ослабить явление параметрического резонанса.
