ДГМ-1раздел(ТВ, статистика)

Раздел 1 Теория вероятностей, математическая статистика, теория надежности

Лекция №1 Элементы теории вероятностей

Структура лекции

1.Общие понятия

2.Алгебра событий

3.Свойства вероятности

4.Одномерные случайные величины

5.Свойства функции распределения случайной величины

Введение

Практически для любых объектов в области электротехники и электроэнергетики на всех этапах жизненных циклов элементов и систем встречаются ситуации, исход которых не может быть точно спрогнозирован. Причиной тому является большое множество факторов, которые влияют на исход, но не могут быть учтены по различным причинам. Такими причинами могут являться неизвестные законы действия величин на исход, невозможность наблюдения величины, сама по себе множественность, требующая увеличения вычислительных ресурсов для прогнозирования.

Например, момент выхода из строя электрической машины определяется внутренними условиями (технологическими отклонениями или наличием дефектов производства, старением и износом элементов конструкции) и внешними условиями (нагрузкой, качеством подводимой энергии, климатическими условиями, действием персонала), каждые из этих условий также зависят от множества других. В силу этих причин исход не может быть определен однозначно. При наличии неопределенности или неоднозначности исхода говорят, что данный исход случаен.

Неопределенность исходов значительно усложняет управление, например управление качеством выпускаемой продукции, управление режимами электроэнергетических систем.

Выявлением и изучением закономерностей в случайных явлениях занимается специальная область математики – теория вероятностей, а методами систематизации и использованием статистических данных, в том числе в управлении – математическая статистика.

Теория вероятностей не дает возможности предсказания отдельного исхода, однако методы теории вероятностей позволяют предсказать

1

суммарный результат, поскольку по их сущности предназначены для исследования массовых явлений.

1. Общие понятия

Современное построение теории вероятностей как раздела математики основывается на аксиоматическом подходе и опирается на элементарные понятия теории множеств. Теория вероятностей оперирует с действительными или мысленными опытами, имеющими случайный исход.

Одним из основных понятий теории вероятностей является случайное событие или просто событие.

Событие – первичное понятие в теории вероятностей в том смысле, что его нельзя определить через другие, более элементарные понятия.

Все события можно разделить на три группы: достоверные, невозможные и случайные (возможные). Достоверное событие – такое событие, которое в данных условиях произойдет обязательно. Например, если бросить игральную кость, то достоверно, что число выпавших очков будет натуральным числом от 1 до 6. Невозможно, выпадение другого числа, а событие выпадения какого-то конкретного, например 1, является случайным. Другим примером случайного события является короткое замыкание в электрической сети, которое не является ни достоверным для определенного момента времени, ни невозможным.

Случайные события могут быть численно охарактеризованы. С

математической точки зрения числовая характеристика возможности появления определенного события в многократно повторяющихся испытаниях называется вероятностью.

Под испытанием (опытом, экспериментом) будем понимать осуществление какого-либо определённого комплекса условий, который может быть воспроизведен сколь угодно большое число раз.

Дадим ряд определений для событий, придерживаясь терминологии и обозначений, принятых в теории вероятностей. События принято обозначать буквами А, В, С, ...

Случайные события

Два события А и В называются несовместными, если они не могут произойти одновременно. Если события А и В могут произойти одновременно, они называются совместными.

Вероятность случайного события

Для случайного эксперимента, который может завершиться одним из п возможных событий, при отсутствии оснований считать одно событие

2

вероятнее другого, такие события называются равновероятными. В простейшем примере о бросании игральной кости возможности выпадения каждой из шести граней (m=6) равновероятны.

Пусть т из этих событий приводят к наступлению события А. Будем называть такие события благоприятными для события А. В примере о бросании игральной кости для события А – выпадение нечетного числа, бла- гоприятных событий три: выпадение грани, содержащей одно очко, грани с тремя очками и грани с пятью очками (т=3).

Эти понятия позволяют дать классическое определение вероятности случайного события.

Определение. Пусть множество исходов опыта состоит из п независимых равновероятных событий. Если m из них благоприятствуют

событию А, то вероятностью события А называется число

Из 1.1 следует, что вероятность достоверного события равна 1 (m=n), а вероятность невозможного – 0 (m=0).

Пример Задача 1.1. Монета подбрасывается два раза. Определить вероятность

выпадения в обоих случаях решки.

Решение

Для определения вероятности события А (выпадение в обоих случаях решки) определим общее число исходов n и число исходов т, благоприятствующих событию.

Общее число исходов n=4: 1) решка-решка, 2) решка-герб, 3) герб- герб, 4) герб-решка.

Число исходов т, благоприятствующих событию A, равно 1. Учитывая, что события выпадения решки и выпадения герба

равновероятны получим = = 1.

4

Во избежание неясностей при описании случайных явлений, результатов опыта или наблюдений необходимо формализовать эти описания. С этой целью вводится множество элементарных исходов эксперимента (пространство элементарных событий).

Совокупность (множество) всех мыслимых исходов опыта, таких, что в результате испытания может произойти один и только один из них, назовем

пространством элементарных событий и будем обозначать его . Каждый

3

элемент ω є (отдельный исход опыта) будем называть элементарным событием.

Пространство элементарных событий является первоначальным понятием при построении математической модели явлений, имеющих случайную (стохастическую) природу.

Любое подмножество множества элементарных событий называется

событием (или случайным событием).

В дальнейшем утверждение «А есть подмножество 2» записывается в виде . Говорят, что событие А наступило, если результатом испытания

дополнением, если оно происходит тогда и только тогда, когда не происходит событие A.

2. Алгебра событий

К множествам событий могут быть применены элементарные алгебраические операции: сложение, произведение. Для наглядности воспользуемся диаграммой Венна–Эйлера (рисунок 1.1). Прямоугольником будем изображать множество элементарных исходов. Каждая точка внутри прямоугольника – элементарное событие ω є . Событие A є будем обозначать областью внутри прямоугольника.

Событие C будет называется суммой или объединением событий A и B, если оно происходит тогда и только тогда, когда происходит по крайней мере одно из событий A или B:

= + =

На диаграмме событие C обозначено заштрихованной областью (рисунок 1.1). Определение справедливо для любого количества слагаемых.

Следствиями определения сложения являются

+ = + ;

+ + = + + ;

+ = ;

+ Ω = Ω;

+ ̅= ; + = Ω.

4

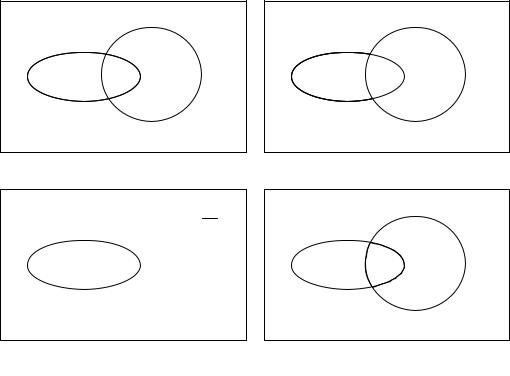
Событие C называется произведением A и B, если оно происходит

· = ;

· Ω = A;

· ̅= ; · = .

Рисунок 1.1 Диаграммы пояснения алгебры событий

Событие C называется разностью A и B, если оно происходит тогда и

− = A;

− ̅= ;

− = ;

−= .Ω

5

Помимо уже отмеченных, справедливы и следующие свойства

+ .

Пример

Задача 1.2. Для системы, состоящей из трех блоков a, b, c, где a и b дублирующие друг друга элементы (схема последовательно соединенных блока c и блока параллельно соединенных a, b).

Записать события 1) система исправна, 2) система неисправна.

Решение

Введем обозначения событий: A – элемент a исправен; B – элемент b исправен; C – элемент c исправен; S – система исправна; Sab – блок элементов a, b исправен.

Система исправна, если исправен элемент c и блок элементов a, b, то есть

= .

из них обязательно случается в результате опыта. Иначе говоря, события

6

, , … образуют полное множество, если их сумма образует

достоверное событие

= = Ω.

Рисунок 1.2 Диаграммы принадлежности и несовместности

3. Свойства вероятности

Свойство 3. Если событие A влечет за собой событие B, то есть , то вероятность события C, где C – разность событий B и A, определяется

Свойство 4. Если событие A влечет за собой событие B, то есть , то вероятность события A не может быть вероятности события B

7

≥ .

Свойство 5. Вероятность любого события заключена между нулем и единицей (аксиомы 1, 2 и свойство 4).

Свойство 6. Вероятность суммы любых двух событий равна сумме

4. Одномерные случайные величины

Событие является качественной характеристикой результата случайного опыта. Между тем, случайный результат опыта можно характеризовать и количественно, если ввести соответствие между элементарными исходами и некоторыми числами. Количественной характеристикой случайного опыта является случайная величина.

Принято определять случайную величину как числовую функцию, определяемую на множестве элементарных событий.

Случайная величина – числовая функция = ( ) со значениями в (одномерном пространстве, обладающем евклидовой структурой), определённая на пространстве элементарных событий .

При таком определении на случайные величины распространяются все правила действий с обычными функциями: их можно складывать, вычитать, перемножать и т.д.

Пример

Если обратиться к задаче 1 с подбрасыванием монеты два раза, то числовая функция = ( ), для элементарных исходов события выпадение решки или герба может быть число выпавших гербов. Тогда следующим исходам будут поставлены в соответствие числовые значения 1) решка- решка (0), 2) решка-герб (1), 3) герб-герб (2), 4) герб-решка (1).

8

Любое событие может быть охарактеризовано случайной величиной. Справедливо и обратное: каждое значение случайной величины можно трактовать как событие, причём различным значениям соответствуют непересекающиеся события.

Случайная величина считается определённой, если известен закон её распределения.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями или множеством значений случайной величины и соответствующими вероятностями.

Взаконе распределения содержится основная и важная информация о случайной величине. Из него можно получить практически все возможные сведения о случайной величине.

Взависимости от возможных значений, принимаемых случайной величиной, и характера закона распределения действительные случайные величины можно разделить на три группы: дискретные, непрерывные и непрерывно-дискретные (смешанные).

Итак, мы приходим к выводу, что для полной характеристики той или иной случайной величины как таковой необходимо и достаточно знать:

1)перечень всех возможных значений этой случайной величины,

2)вероятности, соответствующие этим значениям (или множеству

значений).

Наиболее общей формой закона распределения случайной величины

геометрическую интерпретацию. Если рассматривать случайную величину как случайную точку оси Ох, которая в результате эксперимента может занять то или иное положение, то функция распределения есть вероятность того, что случайная точка попадёт левее точки x.

Функция распределения – универсальная характеристика случайной величины. Ее иногда также называют интегральной функцией распределения или интегральным законом распределения.

Функция распределения существует для всех случайных величин: как дискретных, так и непрерывных. Поясним термины дискретной и непрерывной случайной величины.

Случайная величина является дискретной, если множество ее возможных значений конечно или счётно (счетное множество – такое множество, элементы которого могут быть пронумерованы).

9

Пример

рассматриваемые события несовместны, то они образуют полную группу событий, то есть никаких других событий произойти не может.

Функция называется плотность распределения вероятности либо плотность вероятности.

Пример

Длительность короткого замыкания в распределительной сети. Количество недоотпущенной потребителю электроэнергии. Время простоя оборудования.

5. Свойства функции распределения случайной величины

Свойство 1. Функция распределения есть неубывающая функция своего аргумента, то есть если > , то ≥ ≥ 0.

Из первой аксиомы теории вероятностей вероятность любого событиянеотрицательна. В то же время событие < влечет за собой событие

< , тогда согласно свойству 4 вероятностей < ≤ < .

Свойство 2. На минус бесконечности функция распределения равна нулю (поскольку событие < −∞ является невозможным событием)

−∞ = 0

Свойство 3. На плюс бесконечности функция распределения равна единице (поскольку событие < +∞ является достоверным событием)

+∞ = 1

10