ДГМ-1раздел(ТВ, статистика)

Вероятность безотказной работы или надежность, двигателя в период износа по первому уравнению (1.21) для трех промежутков времени работы после периода нормальной эксплуатации будет:

(где интегралы вероятности из табл. П-1: Ф(-1,41) =-0,9523; Ф(4,26) = 1 ) ;

Общая вероятность безотказной работы, или надежность, двигателя в период износа будет равна произведению надежностей периодов нормальной эксплуатации и износа:

8000 = 8000 8000 = 0,887 · 0,976 = 0,866;

О И

10000 = 10000 10000 = 0,861 · 0,839 = 0,722;

О О 12000 = 12000 И И 12000 = 0,835 · 0,5 = 0,418.

Интенсивность отказов двигателя по третьему уравнению (1.21) для трех промежутков времени в период износа будет:

31

10000 14,2 ) 10 ч ; 12000 39,8 ) 10 ч .

Как показывают полученные данные, надежность рассмотренного двигателя в период износа характеризуется тем, что в соответствии со вторым уравнением (1.21) на каждые 100 двигателей вероятность выхода из строя к концу срока долговечности (Tр=12000 ч) составляет 58 двигателей, или 58%, т.е. более половины двигателей к этому сроку откажет в работе.

Наряду с этим и интенсивность отказов данных двигателей в период износа с течением времени непрерывно и значительно возрастает, что указывает на ускорение процесса их износа по мере приближения времени работы к установленному сроку долговечности.

3. Распределение Рэлея

При изменении во времени отказов технического устройства в соответствии с распределением Рэлея их частота a(t) или плотность вероятности отказов f ( t ) определяются

(1.22)

следующим уравнением:

где σ1 – параметр распределения Рэлея.

32

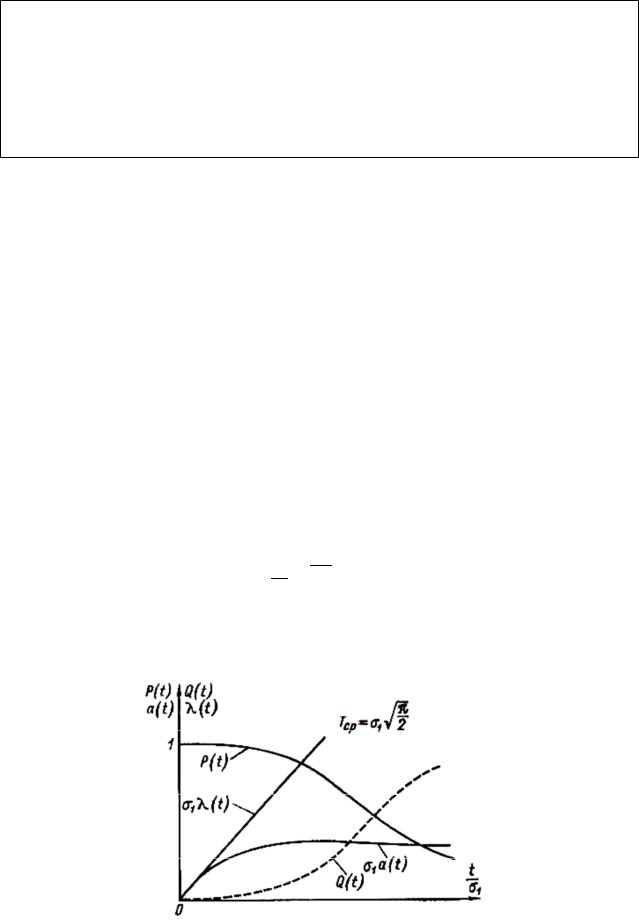
Рис. 1.7. Количественные характеристики надежности технического устройства по распределению Рэлея

В этом случае вероятность безотказной работы устройства Р( t ) , вероятность отказов его Q(t), интенсивность отказов λ(t) и средняя наработка до первого отказа Tср на основании уравнений (1 .2), (1.6), (1.8) и (1 .14), с учетом уравнения (1.22), будут:

1 - %СР = )2/* 1 .

На рис. 1.7 представлены по уравнениям (1.22) и (1.23) количественные характеристики надежности и других величин технического устройства, изменяющиеся во времени по распределению Рэлея. Как показывает рисунок, интенсивность отказов устройства σ1λ(t) по этому распределению возрастает линейно с течением времени. Это означает, что при изменении отказов во времени по распределению Рэлея происходит интенсивное старение, или износ технического устройства и отказы его не удовлетворяют условиям установившегося случайного процесса. При этом вероятность безотказной работы устройства для больших промежутков времени t уменьшается значительно быстрее, чем при экспоненциальной зависимости. Однако в начальный период работы устройства при малых значениях времени t, когда интенсивность отказов незначительна, вероятность безотказной работы P(t) убывает с течением времени медленнее, чем по экспоненте (рис. 1.7). Такое изменение надежности во времени может наблюдаться, например, в некоторых автоматических системах кратковременного действия с резервированием, в которых изменение отказов во времени отдельных элементов системы подчиняется приблизительно распределению Рэлея.

Вэлектрических машинах, в которых при длительной работе обычно наблюдаются случайные внезапные отказы примерно постоянной интенсивности λ, вероятность безотказной работы их как целого устройства P(t) не может практически представляться распределением Рэлея.

Вцелях иллюстрации использования уравнении (1.23) для определения количественных характеристик надежности некоторого технического устройства приводится числовой пример.

33

Пример 1.3. Определить вероятность безотказной работы, интенсивность отказов и среднюю наработку до первого отказа технического устройства, отказы которого во времени подчиняются распределению Рэлея, для трех промежутков времени его работы: t = 200, 1000 и 3000 ч, если параметр распределения σ1= 1500 ч.

Решение

Вероятность безотказной работы, или надежность, устройства по первому уравнению (1.23) для трех промежутков времени работы будет:

Интенсивность отказов устройства по третьему уравнению (1.23) для трех

%Средняя)*наработка1 )*до первого отказа по последнему уравнению (1.23) будет

СР = /2 = /2 · 1500 = 1880 ч.

Как показывают полученные данные, рассмотренное устройство имеет высокую надежность при малых интервалах времени работы и весьма низкую – при больших интервалах, так как интенсивность отказов здесь возрастает пропорционально времени. Следовательно, технические устройства с отказами во времени, подчиняющимися распределению Рэлея, целесообразно использовать только в течение небольших промежутков времени работы.

34

4. Гамма-распределение

Рис. 1.8. Количественные характеристики надежности технического устройства по γ-распределению

Вероятности безотказной работы показаны сплошными линиями, вероятности отказов – штриховыми линиями.

При этом распределении частота отказов технического устройства a(t) или

где λ1 – параметр γ-распределения.

В этом случае при целом и положительном k вероятность безотказной работы устройства P(t), вероятность отказов его Q(t), интенсивность

Параметр k характеризует асимметрию и выход величин за пределы γ- распределения. В зависимости от его значения существенно изменяется вид основных количественных характеристик надежности. На рис. 1.8 представлены построенные по уравнениям (1.24) и (1.25) количественные характеристики надежности и другие величины технического устройства, изменяющиеся во времени по γ-распределению при значениях параметра k≥1. Как показывает первое уравнение (1.25), при k=1 γ- распределение становится чисто экспоненциальным.

35

На практике к γ-распределению близко подходит характер изменения во времени отказов сложных резервированных систем. В целях иллюстрации использования уравнений (1.25) для оценки надежности некоторой резервированной системы приводится числовой пример.

Пример 1.4. Во время контрольных испытаний некоторой системы на заводе-изготовителе обнаружились отказы в ее работе, по характеру приближенно подчиняющиеся γ-распределению с параметром асимметрии k>1. Определить вероятность безотказной работы системы и интенсивность ее отказов для двух промежутков времени: t = 200 и 1000 ч, а также вычислить среднюю наработку ее до первого отказа, если параметры λ0=10-3 ч-1 и k=2.

Решение

Вероятность безотказной работы, или надежность, системы по первому уравнению (1.25) для указанных двух промежутков времени работы будет:

200 = $ 1 + 200 · 10 = 1,2$ , = 0,910;1000 = $ 1 + 1000 · 10 = 2$ = 0,738.

Интенсивность отказов системы для тех же промежутков времени по

Средняя наработка до первого отказа системы по последнему уравнению

(1.25) будет

%СР = 2 = 2000 ч. 10

Как показывают полученные данные, уровень надежности системы с увеличением промежутка времени работы заметно понижается, а интенсивность ее отказов возрастает.

5. Распределение Вейбулла

При этом распределении частота отказов технического устройства a(t) или

плотность вероятности их f(t) представляется следующим уравнением

36

где λ0 – параметр, определяющий масштаб, k – параметр асимметрии распределения.

Рис. 1.9. Количественные характеристики надежности технического устройства по распределению Вейбулла

Вероятности безотказной работы показаны сплошными линиями, вероятности отказов – штриховыми линиями.

В этом случае вероятность безотказной работы устройства P(t), вероятность отказов его Q(t), интенсивность отказов λ(t) и средняя наработка до первого отказа TСР на основании уравнений (1.2), (1.6), (1.8) и

где Г 1 ! 12 – γ-функция, определяемая по табл. П-2 по значению (1/ k +1) .

На рис. 1.9 представлены по уравнениям (1.26) и (1.27) количественные характеристики надежности и других величии технического устройства, изменяющиеся во времени по распределению Вейбулла. При значении параметра k=1 распределение Вейбулла превращается в экспоненциальное распределение; при k>1 интенсивность отказов начинается с нуля и возрастает с течением времени; при k<1 интенсивность отказов начинается с +∞ и с течением времени стремится к нулю. При значении k=2 распределение Вейбулла превращается в распределение Рэлея. К распределению Вейбулла можно приближенно отнести изменение во времени надежности шарикоподшипников, вакуумных приборов и элементов электроники. В целях иллюстрации использования уравнений

37

(1.27) для оценки надежности электрической машины приводится числовой пример.

Пример 1.5. Частота отказов во времени электрической машины на шарикоподшипниках приближенно подчиняется распределению Вейбулла с параметрами k=1,5 и λ0=2·10-6 ч-1,5. Определить вероятность безотказной работы машины и интенсивность ее отказов для трех промежутков времени работы t = 500, 1000 и 2000 ч, а также вычислить среднюю наработку до первого отказа.

Решение.

Вероятность безотказной работы, или надежность, машины по первому уравнению (1.27) для указанных трех промежутков времени работы будет:

Интенсивности отказов машины по третьему уравнению (1.27) для тех же

Средняя наработка до первого отказа по последнему уравнению (1.27)

Как показывают полученные данные, с увеличением продолжительности режима работы электрической машины на шарикоподшипниках происходит непрерывное возрастание интенсивности ее отказов λ(t) и уровень надежности такой машины понижается быстрее, чем при экспоненциальном распределении.

6. Биномиальное распределение

Это распределение по своей форме описывает появление событий, имеющих два исхода, взаимно исключающих друг друга. Этими исходами в каких-то событиях могут быть такие признаки, как «хороший» или «плохой», «черный» или «белый», «исправный» или «неисправный» и т.п. Если,

38

например, в партии из 100 изделий 90 – годных и 10 – бракованных, то вероятность появления тех и других выражается в виде 0,90 годных изделий и 0,10 – бракованных. Сумма вероятностей появления годных и бракованных

Если из большой партии одинаковых изделий, содержащей p% неисправных, берется выборка в количестве n изделий, то вероятность появления

где 6 = &% – доля единицы неисправных изделий в партии, а q – доля

исправных.

В уравнении (1.30) первый член qn показывает вероятность отсутствия неисправных изделий в выборке объемом из n образцов, второй член n·qn-1·p дает вероятность появления в выборке одного неисправного изделия, третий

член n (n −1) q n−2 p 2 – вероятность появления в выборке двух неисправных

2!

изделий.

Для иллюстрации применения биномиального разложения по уравнению (1.30) для оценки вероятности появления неисправных изделий при выборке нескольких из образцов большой партии приводится числовой пример.

Пример 1.6. Из большой партии сельсинов типа НС-404, содержащей p%=5% неисправных образцов, берется для использования в объекте выборка из четырех машин (n=4). Определить вероятности появления в выборках 0, 1, 2,

3 или 4 неисправных сельсинов: p = p% = 0,05 , q=0,95 при этом(q + p)4 = 1 .

100

Решение. Вероятность появления в выборке 0 неисправных сельсинов q4= (0,95)4= 0,8145.

Вероятность появления в выборке 1 неисправного сельсина

4· q3· p = 4·(0,95)3·0,05= 0,1715.

Вероятность появления в выборке 2 неисправных сельсинов

6· q2· p2 = 6· (0,95)2· (0,05)2= 0,0136.

Вероятность появления в выборке 3 неисправных сельсинов

4· q· p3 = 4·(0,95) (0,05) 3= 0,0004.

Вероятность появления в выборке 4 неисправных сельсинов

39

p4 = (0,05) 4= 0,0000.

Полная вероятность равна 1,0000.

Как показывает данный пример, в выборке из партии машин, состоящей из четырех сельсинов, вероятность отсутствия в ней неисправных образцов составляет 0,8145, а вероятность появления в этой выборке четырех неисправных сельсинов равна нулю.

Таким образом, в случае биномиального распределения берут из партии изделий выборку определенного объема n и наблюдают по уравнению (1.30) число появлений какого-то события, например количество неисправных изделий в выборке. При этом число исправных и неисправных изделий в сумме должно равняться объему выборки n.

7. Распределение Пуассона

В случае распределения Пуассона имеют дело с событиями, изолированными во времени или в пространстве. Так, число отказов в работе какого-либо технического устройства в течение некоторого промежутка времени характеризует собой появление изолированных во времени событий.

Распределение Пуассона, как и биномиальное, так же состоит из ряда членов, каждый из которых соответственно определяет вероятность появления 0, 1, 2, 3 или большего числа событий на единицу измерения. При этом сумма этих вероятностей равна единице. Математически распределение Пуассона представляется в следующем виде

где a – среднее значение числа неисправностей на изделие или неисправных изделий в выборке объемом n, определяемое как произведение объема выборки n на среднее значение доли числа неисправностей на изделие или доли неисправных изделий в целой партии p’; следовательно, a=n·p’ – при

$В уравнении (1.31) каждый член левой части означает:

– вероятность появления 0 неисправностей на изделие или неисправных изделий в выборке;

40