ДГМ-4раздел(Диф.ур-ния)

Раздел 4 Дифференциальные уравнения Лекция №1

Аналитические методы решения обыкновенных дифференциальных уравнений

Структура лекции

1.Общие понятия

2.Решение уравнения. Задача Коши

3.Общее и частное решение дифференциальных уравнений

4.Уравнения с разделяющимися переменными

5.Линейные дифференциальные уравнения

6.Уравнения в полных дифференциалах

Введение

Рассмотрим физическое тело, обладающее массой, зарядом и перемещающееся в пространстве с некоторой неизменной скоростью. Тело может взаимодействовать с окружающей средой, если в ней есть электромагнитные и гравитационные поля. Однако в случае их отсутствия процесс на макроскопическом уровне является стационарным: траектория движения, скорость и энергия частицы не изменяется. Описание стационарного процесса производится линейными алгебраическими уравнениями.

Если же на тело действует гравитационные или электромагнитные силы, то под действием этих сил неизбежно будет происходить изменение координат: скорости, энергии и так далее. Такие процессы являются динамическими, и их описание при условиях линейных зависимостей величин и их производных может быть выполнено системой дифференциальных уравнений. Существует очень много систем, процессы в которых являются динамическими и могут быть описаны дифференциальными уравнениями, соответственно и сами дифференциальные уравнения получили широкое распространение.

Примером крупной системы со сложной динамикой является энергетическая система и потребитель электрической энергии. Переходные процессы в этой системе происходят по той причине, что энергия не может изменяться мгновенно, между тем, она запасается в виде магнитной энергии в индуктивных элементах, в виде электрической в емкостных элементах, в виде механической во вращающихся элементах. При возникновении возмущающего воздействия на систему, например короткого замыкания, или

1

управляющего воздействия, например ввод резервного оборудования, начинается перераспределение и изменение энергии. Этот переходный процесс зависит от соотношения инерционных параметров, фактических запасенных энергий и вида и интенсивности воздействия.

Для проектирования и эксплуатации энергосистем, разработки правил, указаний и стандартов необходимо знать эти процессы, а для этого применяется моделирование с использованием дифференциальных уравнений.

1. Общие понятия

Дифференциальные уравнения (ДУ) – это такие уравнения, в которых устанавливается связь значения производной функции (неизвестной функции) с самой функцией, значениями независимых переменных, числами.

В первую очередь, дифференциальные уравнения можно разделить на обыкновенные дифференциальные уравнения (ОДУ) и ДУ в частных производных. В ОДУ неизвестная функция является функцией одной

Дифференциальные уравнения в частных производных – это ДУ, в которых неизвестная функция является функцией нескольких переменных, например

В нашем курсе мы будем рассматривать только обыкновенные дифференциальные уравнения.

Поскольку производная функции сама может являться функцией другого дифференциального уравнения, то при подстановке получается дифференциальное уравнение, в котором от неизвестной функции зависит не только ее первая производная, но и вторая. Число таких подстановок теоретически не ограничено. Наивысший порядок производной, полученный при таких подстановок, называют порядком дифференциального уравнения.

Приведем примеры уравнений первого и второго порядка

Уравнения первого порядка

+ = , = .

Уравнение второго порядка

+ 2 + 3 = .

2

Дифференциальные уравнения первого порядка

Уравнения вида

, , = 0,

где y’ – производная искомой функции y по независимой переменной x, называется дифференциальным уравнением первого порядка.

Если уравнение можно решить относительно старшей производной

искомой функции, то его можно записать в виде

= , или = , .

Данный вид называется уравнением первого порядка, разрешенным относительно производной.

В некоторых случаях дифференциальное уравнение удобно записать в виде dy/dx=f(x, у) или в виде f(x, у) dx - dy = 0, являющемся частным случаем более общего уравнения Р(х, y)dx+Q(x, y)dy=0, где Р(х, у) и Q(x, у) – известные функции. Уравнение в симметричной форме удобно тем, что переменные х и у в нем равноправны, т. е. каждую из них можно рассматривать как функцию другой.

2. Решение уравнения. Задача Коши

Нахождение неизвестной функции y есть решение дифференциального уравнения.

Определение

Решением дифференциального уравнения первого порядка является всякая функция y=ϕ(x), которая при подстановке в уравнение обращает его в тождество.

Рассмотрим простой пример. Функция

у = 7

является решением уравнения

у − 3 = 0.

При подстановке получаем тождество.

3 · 7 − 3 · 7 ≡ 0.

Как видно, тождество сохраняется при любом коэффициенте вместо семерки, это означает наличие бесконечного множества решений.

Рассмотрим теперь задачу нахождения единственного решения.

Теорема Коши

Если в дифференциальном уравнении, решенном относительно старшей производной правая часть и ее частная производная определены и непрерывны в некоторой области G плоскости Oxy, то какова бы ни была внутренняя точка области G, существует единственное решение данного

3

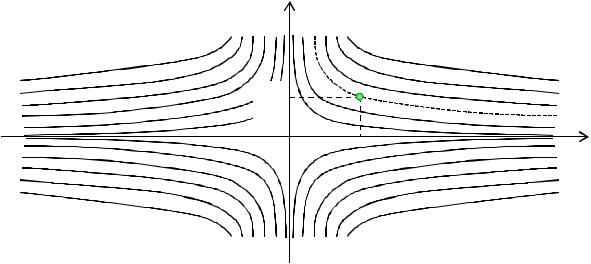
уравнения, удовлетворяющее условию прохождения графика решения уравнения через эту внутреннюю точку.

Рассмотрим на примере уравнения y’=x. Функция f(x, y), равная независимой переменной x и ее производная по у, равная нулю, определены на всей плоскости Oxy. Прохождение через внутреннюю точку x0, y0 обеспечивается выполнением условия y при x равном x0 равно y0. Нахождение решения удовлетворяющего этому условию называется задачей Коши.

Для того чтобы разделить эти понятия введем термины общего и частного решения дифференциального уравнения.

Общим решением ДУ в некоторой области G называется функция y=ϕ(x,C) зависящая от независимой переменной x и одной произвольной постоянной C, если эта функция является решением ДУ при любом значении постоянной C и если при любых начальных условиях таких, что (x0;y0) принадлежит G, существует единственное значение постоянной С=С0 такое что функция y равное y=ϕ(x,C0) удовлетворяет данным начальным условиям y0=ϕ(x0,C0).

Частным решением ДУ в некоторой области G называется функция, которая получается из общего решения при определенном значении постоянной С=С0.

Геометрически общее решение может быть представлено в виде семейства интегральных кривых.

y

y0

x

Рисунок 1.1. Семейство интегральных кривых для решения уравнения

= − /

4. Уравнения с разделяющимися переменными

Определение

Уравнение, которое может быть приведено в виду

4

=

где f1(x), f2(y) – непрерывны функции, зависящие только от одного аргумента, называется дифференциальными уравнением с разделяющимися переменными.

Для отыскания решения дифференциального уравнения нужно

и проинтегрировать обе части уравнения каждую по своей переменной, при этом в правой части уравнения получаем дополнительное

Пример

Требуется найти общее и частное решения уравнения

= / ,

если x0=1 y0=2

Введем функции

= 1 , = .

Тогда можно определить общее решение путем интегрирования.

Проинтегрировав получаем следующее уравнение в логарифмах ln| | = ln| | + или ln| | = ln| | + ln ,

которое можно привести к форме

= .

Решим задачу Коши выразив С из общего решения и подставив

нулевые значения x и y

= = 21 = 2.

Получаем частное решение дифференциального уравнения y=2x.

5. Линейные дифференциальные уравнения

5

где p(x), f(x) – непрерывны функции, называются линейными дифференциальными уравнениями первого прядка.

Если правая часть уравнения равна нулю f(x)=0, то уравнение называют однородным, если не равна, то неоднородным дифференциальным уравнением первого порядка.

Решения таких уравнений может быть выполнено методом вариации постоянной. Для этого сначала находится общее решение линейного

однородного дифференциального уравнения, как уравнения с разделяющимися переменными.

= + .

Полученное общее решение относительно варьируемой постоянной

подставляют в общее решение однородного дифференциального уравнения

= + .

6. Дифференциальные уравнения в полных дифференциалах

В таких уравнениях, как и в уравнениях в частных производных неизвестная функция является функцией двух переменных, однако сумма производных по независимым переменным равна нулю.

Определение

Уравнение вида , + , = 0

где левая часть представляет собой полный дифференциал некоторой функции F(x,y) в некоторой области G, называется уравнением в полных дифференциалах.

Если данное уравнение является уравнением в полных дифференциалах, то его можно записать в следующем виде

6

dF(x,y) = 0,

где F(x,y) такая функция, что ее производная равна P(x,y)dx + Q(x,y)dy. Отсюда видно, что F(x,y)=C является общим решением

дифференциального уравнения.

Если y=ϕ(x), является решением уравнения в полных дифференциалах, то dF(x, ϕ(x))=0, а F(x, ϕ(x))=C. Тогда для того чтобы выражение P(x,y)dx=Q(x,y)dy было полным дифференциалом некоторой функции F(x,y) достаточно, чтобы выполнялось равенство dP/dy=dQ/dx.

Решение находят сначала путем интегрирования первого из

уравнений, при этом постоянную заменяют на функцию от y

, = , + .

После чего полученное решение дифференцируют по y и

Вопросы для самоконтроля

1.Какие процессы описываются с помощью дифференциальных уравнений?

2.Какие уравнения называются дифференциальными?

3.В чем состоит отличие обыкновенных дифференциальных уравнений от дифференциальных уравнений в частных производных?

4.Как определить порядок дифференциального уравнения?

7

5.Что является решением дифференциального уравнения?

6.Поясните термины общее решение и частное решение дифференциального уравнения.

7.Перечислите виду дифференциальных уравнений, решение которых рассмотрено в данной лекции.

8

Лекция №2 Применения операционного исчисления для решения линейных

дифференциальных уравнений

Структура лекции

1.Общие понятия

2.Образы простых функций

3.Свойства преобразования Лапласа

4.Порядок применение преобразования Лапласа

Введение

Как возможно было замечено, нахождение аналитического решения дифференциальных уравнений является достаточно трудоемкой задачей. Если же некоторая система, в которой сигнал подвергается многократным последовательным линейным преобразованиям, описывается системой дифференциальных уравнений, то их анализ становится сложной трудоемкой задачей.

Альтернативой такому подходу к анализу систем является их анализ в операторном пространстве. Математическая основа этого анализа заложена в лекции 3 раздела «Спектральные преобразования и гармонический анализ сигналов», и кроется в преобразовании Лапласа и интеграле Ньютона.

При преобразовании системы дифференциальных уравнений в операторное пространство получается система линейных уравнений алгебраических уравнений. Решение этой системы намного более простая задача, однако требуется преобразования из оригиналов функций в их изображения и обратно, что является непростой задачей.

В то же время преобразование обратно в динамическую форму не всегда требуется, поскольку частотные критерии позволяют производить анализ динамических свойств в частотной области.

1. Общие понятия

В основе операционного исчисления лежит преобразование Лапласа (см. раздел 3 лекция 3).

Сделаем напоминание

Изображением (лаплас-образом) комплексной функции f(t) (оригинала) вещественного аргумента t, 0≤t<∞, в пространстве Лапласа является функция F(p) от комплексной переменной p=σ+jω.

9

Формула для нахождения образа называется преобразованием Лапласа.

= ( ) .

Математически связь между изображением и первообразной функции

будем записывать следующим образом

→ .

Для сходимости интеграла необходимо, чтобы f(t) при конечном значении t была конечна, а при t→∞ была конечна либо ограниченно

нарастала не быстрее экспоненты, то есть

|| ≤

где M и s0 – некоторые постоянные. | |

В этом случае существует такое σ, при котором ( ) будет стремиться к нулю при t→∞.

| ( )| = ( ) = | ( )| ≤ ( )

То есть F(p) определена в полуплоскости Re(p)>s0.

Сделаем важное замечание, которые в дальнейшем будем использовать при формировании образов простых функций и при определении свойств преобразования Лапласа:

из преобразования Лапласа видно, что при сложении оригиналов функций fi(t) складываются и изображения, а при умножении оригинала на константу, на нее же умножается и изображение.

Следствием этого утверждения является то, что если оригинал и изображение зависят от некоторой константы k, то производная по параметру

k оригинала преобразуется в производную изображения по этой константе.

→

2. Образы простых функций

Для удобства применение операционного исчисления можно заранее найти основные функции, используемые при анализе линейных систем. Из этих функций могут быть получены более сложные путем суммирования нескольких функций и умножения функций на масштабный коэффициент.

10