ДГМ-4раздел(Диф.ур-ния)

Такими простейшими функциями являются единичная ступенчатая функция Хэвисайда, дельта-функция, апериодическая экспоненциальная функция, гармоническая функция…

1. Самое простое вычислить образ экспоненциальной функции

2. Опираясь на ранее озвученное следствие преобразования производно по константе при дифференцировании изображения и оригинала

Полагая a = 0 получаем

1

1 → ;

→ ! .

3. Для случая, когда a является комплексной величиной

= +

4. Для периодической функции f(t) с периодом T>0 изображение можно вычислить следующим образом

11

5. Изображение дельта-функции ∂(t)

Дельта-функция это функция, которая принимает значение 0 на интервале значений аргумента (-∞, 0)∩(0, +∞) и +∞, когда значение аргумента равно 0, при этом интеграл дельта-функции в окрестности нуля равен 1.

0

Рисунок 2.1. График дельта функции и интеграла дельта-функции (функции Хэвисайда)

Найдем изображение дельта-функции в операторном пространстве.

Полученные изображения функций сведем в таблицу.

12

Таблица 2.1.

Повторяя дифференцирование получим

→ − +0 − ′ +0 .

Это означает, что производная оригинала преобразуется в умножение изображения на оператор Лапласа. Интеграл от оригинала преобразуется в деление изображения на оператор Лапласа.

13

5. Свертка двух оригиналов функций преобразуется в произведение образов этих функций

→ .

4. Порядок применение преобразования Лапласа

Допустим, что система описывается функциями времени x(t), y(t), …, которые являются искомыми. Однако часто бывает, что уравнения, связывающие образы функций, гораздо проще решить, чем уравнения, описывающие связь оригиналов этих функций.

Тогда решение выполняется в четыре этапа:

1) Составляется уравнение (система уравнений), связывающее оригиналы функций;

2) Производится переход к уравнениям для изображений (в операторном пространстве);

3) Выполняется решение;

4) Производится обратное преобразование изображений в оригиналы.

При начальных условиях x(0)=α, x’(0)=β.

Такое уравнение может быть получено для электрической цепи, содержащей кроме активных элементов, индуктивный и емкостный.

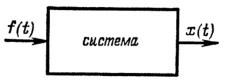
Представим уравнение связи в виде черного ящика

Выполнив преобразование уравнения в операторное пространство получаем

Где X(p) – лаплас-образ искомой функции, F(p) – лаплас-образ заданной функции.

Решением в операторной форме будет

14

&+ + + '

=+ ' + %

W(p)=1/D(p) – называют передаточной функцией.

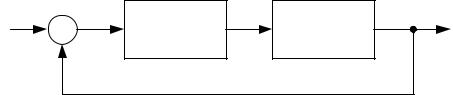
Исходя из этой записи при наличии системы уравнений ее решение можно представить в виде структурной схемы

Для преобразования структурных схем существуют свои правила, однако в результате можно даже вручную достаточно легко найти решение в операторной форме.

На преобразовании Лапласа основывается частотный анализ систем по передаточным функциям. Можно определять по передаточной функции разомкнутой системы запас устойчивости, полосу пропускания и т.д. Можно производить анализ систем по расположению корней числителя (нулей) и знаменателя (знаменателя) передаточной функции. Поэтому нахождение оригинала решения не всегда является необходимой задачей.

Вопросы для самоконтроля

1.Каково условие сходимости интеграла преобразования Лапласа?

2.Следствием какого утверждения является то, что производная по константе от которой зависит оригинал преобразуется в производную изображения по этой константе?

3.Перечислите функции, образы которых были определены в данной

лекции.

4.Перечислите свойства преобразования Лапласа, рассмотренные в данной лекции.

5.Каков алгоритм анализа динамической системы с использованием преобразования Лапласа?

6.Поясните термин передаточная функция.

15

Лекция №3 Численные методы решения дифференциальных уравнений

Структура лекции

1.Общие понятия

2.Классификация численных методов

3.Понятие ошибки и порядок численных методов

4.Устойчивость численных методов

5.Жесткость систем дифференциальных уравнений

Введение

Не для всех дифференциальных уравнений можно найти аналитическое решение. Однако зачастую для решения практических задач достаточно иметь частное решение при конкретных начальных условиях. В этих случаях применяются численные методы решения дифференциальных уравнений. Численные методы позволяют найти приближенное решение дифференциального уравнения (системы дифференциальных уравнений) в том числе и нелинейных.

Рассматривая в качестве примера электроэнергетическую систему можно отметить, что она обладает существенной нелинейностью, помимо нелинейности параметров, зависящих от величины и частоты протекающего тока, температуры (индуктивности шунтирующих реакторов, трансформаторов и электрических машин, активные сопротивления, активные сопротивления обмоток роторов асинхронных электрических машин, нелинейности параметров и зоны нечувствительности и гистерезиса регуляторов и т.д.). Существующие методы, которые позволяют определять свойства системы, требуют предварительно линеаризации дифференциальных уравнений. При значительных нелинейностях это может приводить к неадекватным оценкам, что может стать причиной неправильной настройки систем управления или выбору ее структуры и невозможности ее последующей эксплуатации.

Для учета нелинейности приходится прибегать к численным методам решения дифференциальных уравнений. А поскольку многие системы обладают существенными нелинейностями, то численные методы получили широчайшее распространение и применяются для моделирования процессов динамических систем.

Однако необходимо понимать, что приближенное решение означает неизбежное наличие ошибок в полученном решении. Эти ошибки не могут

16

быть численно определены, когда нет точного аналитического решения. Для применения численных методом есть ряд ограничений размерность системы дифференциальных уравнений, жесткость, длительность интервала моделирования и прочее. Для формирования этого понимания остановимся на общих понятиях о численных методах решения дифференциальных уравнений.

1. Общие понятия

Рассмотрим обыкновенное дифференциальное уравнение первого

для которого заданы начальные условия в виде у(x0)=y0. Его решение (решение задачи Коши) может быть получено точными, приближенными или численными методами.

Численные методы – это алгоритмы вычисления приближенных значений искомого решения у(х) на некоторой выбранной сетке значений аргумента.

• Численное решение задачи ищется на интервале [x0, xn]. Левая граница интервала задана, а правая может быть либо задана, либо определена в процессе расчета каким-либо условием.

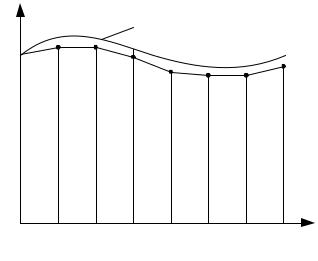
Рисунок 3.1. Точное аналитическое и численное решения дифференциального уравнения

• Искомое приближенное решение ищется в отдельных точках x1, x2, x3,…, xn интервала, называемых узлами сетки, в виде последовательности значений y1, y2, y3,…, yn, приближенно равных последовательности y(x1), y(x2), y(x3),…, y(xn) определяемой точным решением y(t). В общем случае решением системы дифференциальных уравнений является

17

последовательность векторов Y(x1), Y(x2), Y(x3),…, Y(xn), где Y=(y1, y2, y3,…, yq).

• Расстояние между соседними узлами называется шагом интегрирования h=xk+1-xk.

2. Классификация численных методов

Численные методы решения дифференциальных уравнений делятся на явные и неявные методы решения.

Точка Yk+1, определяемая на (k+1)-ой итерации, может вычисляться

явно:

Yk+1=Ф(xk, xk-1,…, xk-m+1, Yk, Yk-1,…, Yk-m+1)

где Ф(…) – некоторая функция, зависящая от конкретного алгоритма, в которой кроме последней рассчитанной точки используются еще (m-1) предыдущих точек

или неявно

Yk+1=Ф(xk, xk-1,…, xk-m+1, Yk+1, Yk, Yk-1,…, Yk-m+1)

где искомая величина Yk+1 входит одновременно и в левую и в правую части уравнения.

Классификация и примеры численных методов решения дифференциальных уравнений приведены на рисунке 3.2.

18

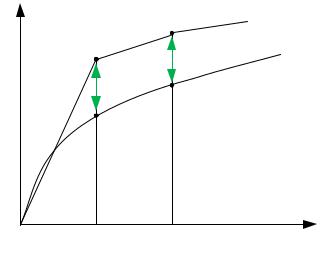
На второй итерации (то же идет на k-й итерации): Y2-Y(x2)= ξ2O+ ξ2M + ξ2П,

где ξ2П – переходная ошибка, обусловленная тем, что при расчете точки Y2 вместо Y(x1) берется приближенное значение Y1, полученное на предыдущей итерации.

Рисунок 3.3. Глобальные ошибки численного решения дифференциального уравнения

Порядок численных методов

Пусть ξN(h) – некоторая функция переменной h с конечной областью определения D на полуоси h>0, причем h может принимать сколь угодно малые значения. Тогда если существуют такие положительные числа h0, C, p, что при всех h, принадлежащих D, удовлетворяющих условию 0<h≤h0, выполняется соотношение | ξN(h)| ≤Chp,

то ξN(h)=O(hp)

Число p называют порядком численного метода, если его глобальная ошибка есть О большое от hp.

4. Устойчивость численных методов

Явление числовой неустойчивости связано с тем, что в течение каждой последующей итерации ошибка интегрирования неуклонно растет.

Устойчивость численных методов проверяется на тестовом примере: y'=λy, y(0)=1,

где λ – в общем случае комплексная константа. Уравнение является простейшим, и любой метод, непригодный для его решения, не представляет интереса.

20