
ДГМ-4раздел(Диф.ур-ния)
.pdf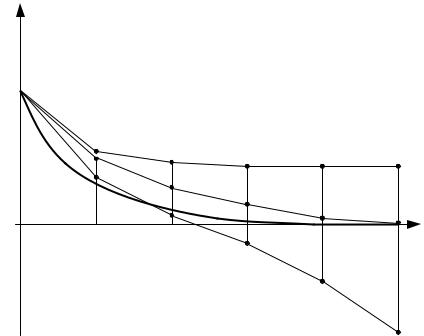
Метод называется устойчивым (ограниченно устойчивым), если существует такое число hкр>0, что при использовании метода для решения тестового примера, где вещественная составляющая λ меньше нуля (Re(λ)<0), с шагом 0<h≤hкр при xk=x0+kh стремящемся в бесконечность, глобальная ошибка ограничена.
Рисунок 3.4. Точное аналитическое и численное решения дифференциального уравнения:
1 – ограничено устойчивое;
2 – неустойчивое;
3 – асимптотически устойчивое.
Величина hкр называется критическим шагом. Если h>hкр, глобальная ошибка может неограниченно возрастать.
Метод называется A-устойчивым (асимптотически устойчивым),
если при его применении все численные решения тестовой задачи с фиксированным шагом h>0 и Re(λ)<0 стремятся к нулю при xk=x0+kh→∞.
6. Жесткость систем дифференциальных уравнений
Аппроксимируем систему дифференциальных уравнений dY/dx=F(x,Y(x)) в некоторой окрестности точного решения Y(x) линеаризованной системой
dY/dx = F(x,Y(x)) + J(x)(Y-Y(x))
21
где J(x) – матрица Якоби, составленная из вычисленных в точке (x, Y(x)) частных производных.
Если изменение J(x) на некотором интервале [x0, xn] достаточно мало, то локальные фундаментальные решения системы приближенно равны eλix, где λi= λi(x) – локальное собственное значение J(x).
Будем предполагать, что система локально устойчива, так что Re(λi)<0 и фундаментальные решения затухают с ростом x со скоростью, пропорциональной величине
1/Re(λi),
которая называется постоянной времени.
Задача Коши называется жесткой на интервале [x0, xn], если для всех xє [x0, xn] выполняется два соотношения
Re(λi)<0, S(t)=max(Re(λi))/ min(Re(λi))>>1
На практике систему дифференциальных уравнений можно считать жесткой, если S(t) является величиной O(10), однако в некоторых прикладных задачах, включая теорию электрических сетей S(t) может достигать величины O(108).
Пример
|
Найти коэффициент жесткости системы дифференциальных |
||||||||||||
уравнений |
|
= 998 + 1998 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
При x0=1, y0=1. |
) |
= −999 − 1999 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим собственные значения матрицы коэффициентов |
|
|||||||||||
|
|
|
* |
|
998 |
1998 |
|
|
|
|
|
|
|
|
|
|
= #−999 − 1999$ |
|
|
|
|
|
|
||||
|
Для этого находим определитель матрицы A-λI, где I – единичная |
||||||||||||
диагональная матрица. |
|
|
|
, |
|
, |
|
|
|
|
|
||
+ |
−999 |
− 1999 − ,+ |
|
|
|
|
|||||||
|
998 − , |
1998 |
= |
|
998 − |
|
−1999 − |
|
− |
|
−999 |
1998 |
= 0 |
|
|
|
, + 1001, + 1000 = 0 |
|
|
|
|
|
|
||||
|
Решаем квадратное уравнение и получаем собственные значения |
||||||||||||
|
λ1=-1, λ2=-1000. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Вещественные |
составляющие |
обоих |
значений |
отрицательные |
||||||||
величины, что свидетельствует об устойчивости решения системы, а жесткость системы равна
S(t)= λ2/λ1=-1000/-1=103>>1.
22
Может показаться, что численное интегрирование заданной системы
можно было бы вести сначала с малым шагом интегрирования, а затем, когда компонента e-1000t станет малой, увеличить шаг. На самом деле это не так.
Компонента решения e-1000t заставляет вести интегрирование с малым шагом на всем интервале. Шаг определяется наименьшей постоянной времени.
Вопросы для самоконтроля
1.Дайте определение численным метода решения дифференциальных уравнений.
2.Что называется шагом интегрирования?
3.Укажите различия явных и неявных методов численного решения дифференциальных уравнений.
4.Какие есть понятия ошибок численного решения дифференциальных уравнений и в чем они состоят?
5.Что называют порядком численных методов?
6.В чем заключается причина неустойчивости численных методов?
7.Поясните понятия ограниченно устойчивого, неустойчивого и асимптотически устойчивого численного метода решения дифференциальных уравнений.
8.Дайте определение понятию жесткости системы дифференциальных уравнений.
23

Лекция №4 Явные методы решения дифференциальных уравнений
Структура лекции
1.Явный метод Эйлера
2.Методы Рунге-Кутта второго порядка
3.Метод Рунге-Кутта четвертого порядка
Введение
В предыдущей лекции были рассмотрены основные понятия теории численных методов решения дифференциальных уравнений. Опираясь на эти понятия, рассмотрим некоторые методы численного решения, определяя их порядок точности относительно шага интегрирования и устойчивость методов.
1. Явный метод Эйлера
Рассмотрим систему обыкновенных дифференциальных уравнений
первого порядка разрешенных относительно производной, для которого заданы начальные условия в виде X(t0)=X0
|
= , &. |
(4.1) |
|
Суть метода Эйлера заключается в переходе от бесконечно малых приращений к конечным, то есть в замене производной приближенным
конечно-разностным отношением |
|
|
|
|
||||||
& |
|
|
= |
|
= |
& − |
& |
= & − & |
= ( , |
) |
|
" |
|
|
|
|
|
|
& |
||
|
|
|
|
− |
|
|||||
|
|
|
|
|
||||||
Отсюда получаем & = & + ( , & ) |
(4.2) |
|
||||||||
Формула |
(4.2) |
|
представляет |
алгоритм |
приближенного решения |
|||||
системы дифференциальных уравнений (4.1), называемый явным методом Эйлера.
Метод Эйлера является ограниченно устойчивым, то есть существует критический шаг интегрирования hкр=Cτmin, где τmin – минимальная постоянная времени, а C = 2. Метод имеет первый порядок точности относительно шага h: ξk(h)=O(h), k=1,…, n.
24
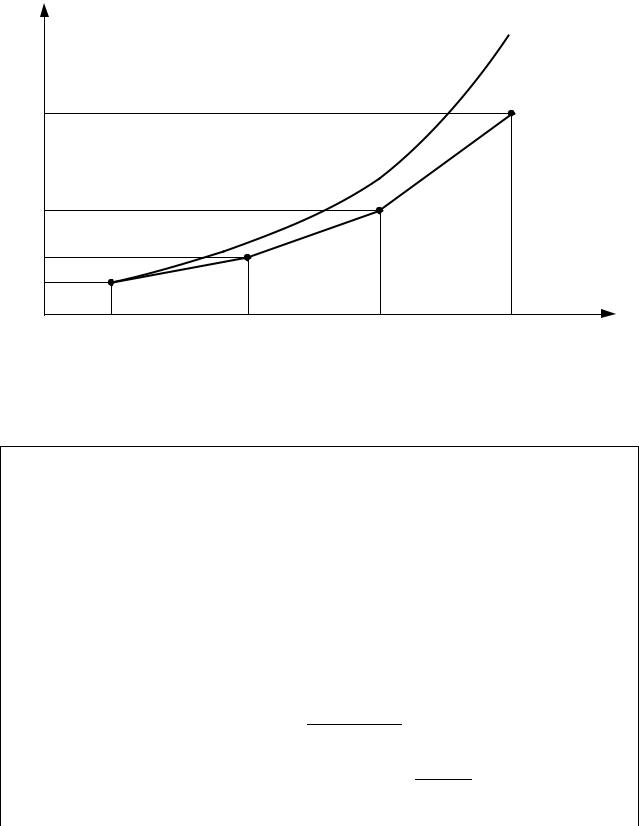
Геометрически метод Эйлера может быть интерпретирован, как замена точного частного решения дифференциального уравнения (интегральной кривой) ломаной линией, представляющей собой отрезки касательных ней в узлах.
Рисунок 4.1. Интегральная кривая для частного решения дифференциального |
уравнения и его численное решение в узлах сетки |
Пример
Приближенно решить дифференциальное уравнение = − / на отрезке [-1, 3] с начальным условием x(-1)=0,21 и шагом h=0,1.
Решение
Стоит отметить, что условие существования решения данного уравнения нарушается при приближении x к нулю, поэтому при решении дифференциального уравнения на каждом шаге требуется проверять условие x≠0 и при невыполнении этого условия прекращать интегрирование.
Рассматриваемое уравнение является уравнением с разделяющимися переменными, поэтому его частное решение, удовлетворяющее начальному
условию, можно получить аналитически
= -1,0441 − .
Анализ частного решения позволяет сделать вывод, что решение рассматриваемой задачи существует для | | < √1,0441. То есть интервал существования решения составляет (-1,0219; 1,0219). Явный метод Эйлера в
25
данной задаче позволяет найти приближенное решение на интервале [-1; 1], с
учетом величины шага h=0,1. |
|
|
|
|
|
|
|
|
||||
|
Формула метода Эйлера из 4.2 получается следующая |
|||||||||||
|
|
& |
& |
|
|
|
& |
|
|
|||
|
|
= |
+ |
|
|
|
= |
+ |
0,1 · |
, |
||
|
|
|
& |
|
||||||||
|
|
= + , |
|
|
|
|
|
|
& |
|
||
|
|
= 1, 2, … , 20, = −1, & = 0,21. |
||||||||||
|
Результат решения приведен в таблице 4.1. |
|
|
|||||||||
Таблица 4.1. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
||||||||||
-1 |
0,21 |
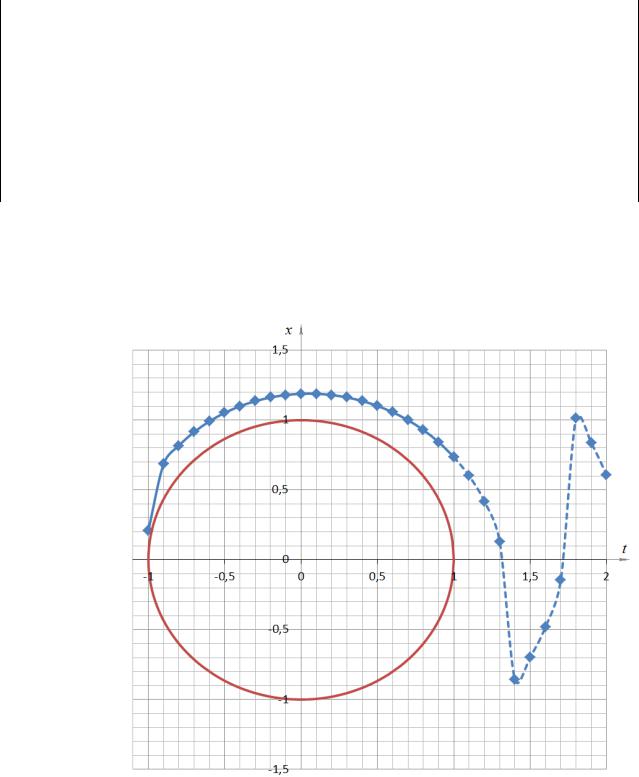
На рисунке 4.2 изображено полученное приближенное |
||||||||||
-0,9 |
0,686 |
решение и точное решение, а пунктирной линией показана |
||||||||||
-0,8 |
0,817 |
кривая, которая получается при продолжении численного |
||||||||||
-0,7 |
0,915 |
|||||||||||
решения задачи без проверки условия существования решения |
||||||||||||
-0,6 |
0,992 |
|||||||||||
(решением не является). |
|
|
|
|
|
|||||||
-0,5 |
1,052 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
-0,4 |
1,100 |
|
|
|
|
|
|
|
|
|
|
|
-0,3 |
1,136 |
|
|
|
|
|
|
|
|
|
|
|
-0,2 |
1,163 |
|
|
|
|
|
|
|
|
|
|
|
-0,1 |
1,180 |
|
|
|
|
|
|
|
|
|
|
|
0 |
1,188 |
|
|
|
|
|
|
|
|
|
|
|
0,1 |
1,188 |
|
|
|
|
|
|
|
|
|
|
|
0,2 |
1,180 |
|
|
|
|
|
|
|
|
|
|
|
0,3 |
1,163 |
|
|
|
|
|
|
|
|
|
|
|
0,4 |
1,137 |
|
|
|
|
|
|
|
|
|
|
|
0,5 |
1,102 |
|
|
|
|
|
|
|
|
|
|
|
0,6 |
1,056 |
|
|
|
|
|
|
|
|
|
|
|
0,7 |
1,000 |
|
|
|
|
|
|
|
|
|
|
|
0,8 |
0,930 |
|
|
|
|
|
|
|
|
|
|
|
0,9 |
0,844 |
|
|
|
|
|
|
|
|
|
|
|
1 |
0,737 |
|
|
|
|
|
|
|
|
|
|
|
1,1 |
0,601 |
|
|
|
|
|
|
|
|
|
|
|
1,2 |
0,418 |
|
|
|
|
|
|
|
|
|
|
|
1,3 |
0,131 |
|
|
|
|
|
|
|
|
|
|
|
1,4 |
-0,859 |
|
|
|
|
|
|
|
|
|
|
|
1,5 |
-0,696 |
|
|
|
|
|
|
|
|
|
|
|
1,6 |
-0,480 |
Рисунок 4.2. Приближенное и численное решение |
||||||||||
1,7 |
-0,146 |
|
дифференциального уравнения |
|||||||||
1,8 |
1,014 |
|
||||||||||
Стоит отметить, |
что |
точность |
решения существенно |
|||||||||
1,9 |
0,837 |
|||||||||||
снижается при приближении решения к нулевому значению. |
||||||||||||
2 |
0,609 |
|||||||||||
26
2. Методы Рунге-Кутта второго порядка
Методы Рунге-Кутта второго порядка основаны на разложении функции в ряд Тейлора и учете трех его первых членов (до второй производной включительно).
Метод Рунге-Кутта второго порядка с полным шагом (метод
предсказания и коррекции) реализуется по формуле
& = & + /2 # , & + / , &0 1$
Метод имеет второй порядок точности относительно шага h:
ξk(h)=O(h2), k=1,…, n.
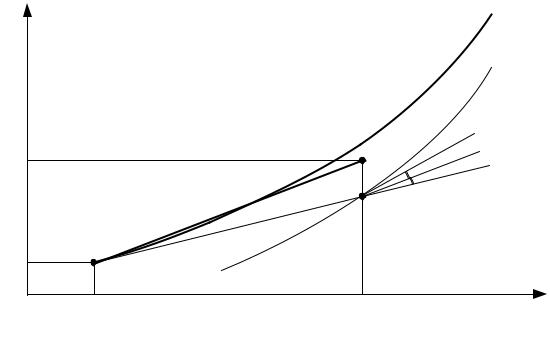
Алгоритм решения и геометрическая интерпретация заключается в следующем (рисунок 4.3):
1. Приближенно вычисляют значение функции в точке tk+h по формуле Эйлера и наклон интегральной кривой в этой точке
&′ = / , &0 1
2. |
Находят средний наклон на шаге h |
|
& + & ; |
|
2 |
3. |
По этому наклону уточняют значение Xk+1. |
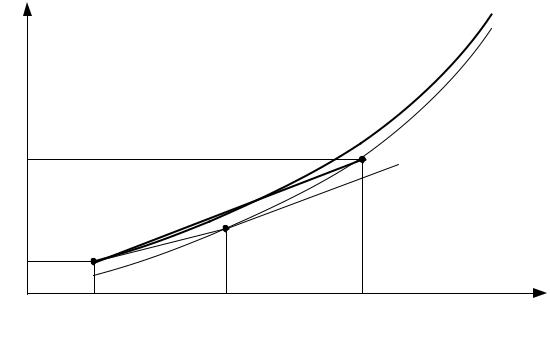
Рисунок 4.3. Интегральная кривая для частного решения дифференциального |
|
|
уравнения и его численное решение в узлах сетки |
27
Метод Рунге-Кутта второго порядка с половинным шагом реализуется по формуле (модифицированный метод Эйлера)
Формул для приближенного решения системы дифференциальных уравнений на (k+1)-ом шаге имеют вид
& = & + /2 / + /2, & / 1
Метод имеет второй порядок точности относительно шага h:
ξk(h)=O(h2), k=1,…, n.
Алгоритм решения и геометрическая интерпретация заключается в следующем (рисунок 4.4):
1. Делают дробный шаг tk+h/2 по формуле Эйлера находят
& / = & + /2 ( , & )
2. В найденной точке определяют наклон интегральной кривой
&′ / = / + /2, & / 1
3. По этому наклону рассчитывается значение Xk+1.
Рисунок 4.4. Интегральная кривая для частного решения дифференциального уравнения и его численное решение в узлах сетки
3. Метод Рунге-Кутта четвертого порядка
Метод Рунге-Кутта четвертого порядка основан на разложении искомого решения y(x) в ряд Тейлора, учитывающий члены, содержащие степени шага h до четвертой включительно.
28

Наиболее распространенный вариант этого метода, заключающийся в
последовательном вычислении на каждом шаге коэффициентов формулы
& = & + 16 + 2 + 2 + ,
где k1, k2, k3, k4 – угловые коэффициенты касательных к графику решения в |
||||
различных точках, вычисляемые по формулам |
|
|
||
= , & , |
|
|
||
= + |
|
, & + |
|
, |
2 |
2 |
|||
= + |
|
, & + |
|
, |
|
|
|||
2 |
2 |
|||
= + , & + .
Метод имеет четвертый порядок точности относительно шага h:
ξk(h)=O(h4), k=1,…, n.
Метод Рунге-Кутта четвертого прядка, как и все методы рассмотренные выше, является одношаговым, так как значения вычисляются на основе текущего значения Xk. Кроме того, эти методы ограниченно устойчивы. Критическое значение шага интегрирования для метода Рунге-Кутта четвертого прядка составляет Для выполнения одной итерации метод Рунге-Кутта четвертого прядка требует четыре раза произвести вычисление правой части. Приведенные методы позволяют легко менять шаг в процессе вычисления.
Вопросы для самоконтроля
1.В чем состоит суть метода Эйлера?
2.Какие еще явные методы решения дифференциальных уравнений были рассмотрены в данной лекции?
3.Каким порядком точности относительно шага интегрирования обладают рассмотренные в лекции методы?
4.Какими с точки зрения устойчивости являются рассмотренные в лекции методы?
Основная учебная литература
1. Вычислительная математика для специалистов наукоемких, высокотехнологичных инновационных предприятий и организаций [Электронный ресурс]: учебное пособие / В. В. Ласуков, С. В. Рожкова; Национальный исследовательский Томский политехнический университет
29
(ТПУ). — Томск: Изд-во ТПУ, 2011. — Электронная версия печатной публикации. — Доступ из корпоративной сети ТПУ.
Схема доступа: http://www.lib.tpu.ru/fulltext2/m/2012/m55.pdf
2.Теория и реализация задач вычислительной математики в пакете MathCad [Электронный ресурс] : учебное пособие / Национальный исследовательский Томский политехнический университет (ТПУ), Институт кибернетики (ИК), Кафедра автоматики и компьютерных систем (АИКС) ; сост. А. И. Кочегуров ; Е. А. Кочегурова. — Томск: Изд-во ТПУ, 2013. — Электронная версия печатной публикации. — Доступ из корпоративной сети ТПУ.
Схема доступа: http://www.lib.tpu.ru/fulltext2/m/2014/m113.pdf
3.Высшая математика. Полный курс [Электронный ресурс]: учебник для бакалавров / В. С. Шипачев. – 4-е изд. — Мультимедиа ресурсы (10 директорий; 100 файлов; 740MB). – Москва: Юрайт, 2013. – 1 Мультимедиа CD-ROM. – Бакалавр. Базовый курс. –Бакалавр. Углубленный курс. – Электронные учебники издательства Юрайт. – Электронная копия печатного издания. – Доступ из корпоративной сети ТПУ.
Схема доступа: http://www.lib.tpu.ru/fulltext2/m/2013/FN/fn-2437.pdf
4.Бибиков, Ю. Н.Курс обыкновенных дифференциальных уравнений [Электронный ресурс] : учеб. пособие / Ю. Н. Бибиков. — Москва: Лань, 2011. — 304 с. Предм. указ.: с. 299-301.. — ISBN 978-5-8114-1176-4.
Схема доступа: http://e.lanbook.com/books/element.php?pl1_cid=25&pl1_id=1542
5.Мышкис, А.Д. Математика для технических вузов : : Учеб. пособие. —
Москва: Лань, 2009. — 640 с.. — ISBN 978-5-8114-0395-0: 690-00.
Схема доступа: http://e.lanbook.com/books/element.php?pl1_cid=25&pl1_id=282
6.Обыкновенные дифференциальные уравнения в примерах и задачах: учеб. пособие / А.В. Пантелеев, А.С. Якимова, А.В. Босов. – М.: Высш.
шк., 2001. – 376 с.: ил.
30
