
- •Линейные волны
- •Волновое уравнение. Бегущие волны
- •Преобразование Фурье.
- •Монохроматическая волна.
- •Характеристики линейных волн.
- •Фазовая скорость линейных волн
- •Дисперсия среды. Групповая скорость линейных волн
- •Явление опрокидывания (укручения) нелинейных волн
- •Преобразование Коула – Хопфа. Ударные волны
- •Асимптотические решения уравнения Бюргерса. Ширина фронта ударной волны
- •Оценки ширины фронта ударной волны. Число Рейнольдса
- •Спектр ударной волны.
- •Солитоны
- •Стационарные волны
- •Солитонные решения волнового уравнения (общие свойства)
- •Солитонное решение уравнения Кортевега - де -Вриза
- •Решение уравнения КдВ (общий вид)
- •Законы сохранения
- •Нелинейные уравнения, обладающие солитонными решениями
- •Нелинейные уравнения, не имеющие решений в виде солитонов.
- •Динамический хаос
- •Нелинейный маятник
- •Характеристики нелинейного маятника.
- •Особенности движения вблизи сепаратрисы
- •Переменные: «Действие» и «угол»
- •Уравнение нелинейного маятника при наличии внешней периодической силы.
- •Перекрытие резонансов. Критерий стохастичности
- •Параметрический резонанс
-
Решение уравнения КдВ (общий вид)
Из выражения:
![]()
![]()
Сведем к уравнению Якоби. Полином имеет 3 корня:
![]()
P(u)>0

![]()
Согласно алгебраическим
выражениям:
![]()
Чтобы существовало
действительное физическое решение
было, должно быть
![]() ,
т.е необходимо
,
т.е необходимо ![]()
Введем новую переменную
![]() =>
=>
![]()
Сделаем замену
переменных, т.к. ![]() ,
то производная g
и u
связаны линейным образом.
,
то производная g
и u
связаны линейным образом.
![]()
Замена:
![]()
![]()
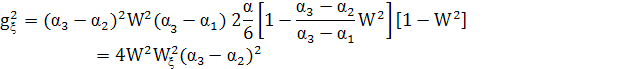
![]()
Обозначим
![]()
Чтобы перейти к уравнению Якоби надо чтобы 1й множитель был равен 1. Заменим независимую переменную:
![]()
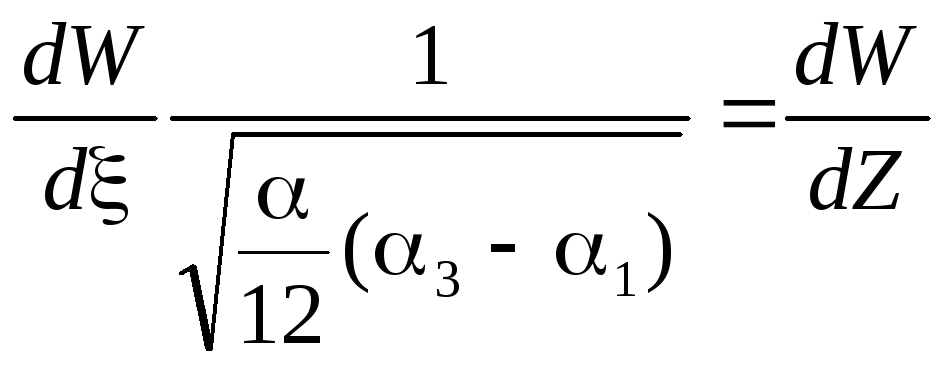
![]()
Решением этого уравнения является специальные функции - эллиптическая функция Якоби Sn(z,k)
Вернемся к ранним переменным
![]()
Полученная формула справедлива для любых граничных условий.
Используя асимптотическую формулу функции Якоби
-
k—> 1
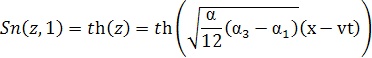
-
при k—>0
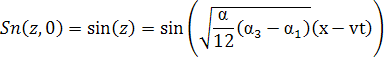
Примем граничные
условия ![]() на
на
![]()
В
этом случае ![]()
=>
![]()
Решение:
U=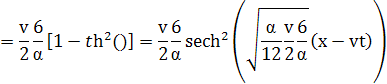
При общих граничных условиях
![]()
-
Законы сохранения
 (1)
(1)
Проинтегрируем и учтем
![]()
Получим:
![]() - инварианта
- инварианта
Эта величина называется интеграл движения или закон сохранения
С наличием законовм сохранения тесно связана устойчивая структура солитона.
Ни все нелинейные уравнения, имеющие решения в виде уединенной волны, обладают солитоным решением. А те уравнения, для которых можно записать бесконечное число интегралов движения обладают солитонным движением.
Любая Гамильтонова система имеет n-частиц и n- степеней свободы.
Если она имеет 3n интегралов движения, то она интегрируема, (т.е. имеет решение).
Интегралы движения получают умножением (1) на U и интегрированием:

Последнее слагаемое
проинтегрируем по частям

Получим:
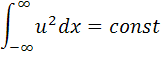
Запишем

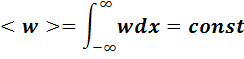
Если перейти к функции
W
и разложить ее по параметру
![]() :
:
![]() ,
,
Где ![]() -
не зависит от
-
не зависит от ![]()
И где
![]() ,
,![]() ,
,![]()
Тогда из того что![]()
![]()
Т.е. бесконечное количество интегралов движения можно найти
-
Нелинейные уравнения, обладающие солитонными решениями
-
Уравнение КДВ и его модификации.
-
Уравнение sin – Гордон:
Вид:
![]()
Имеет солитонное
решение:
![]() ,
где
,
где
![]()
//![]() - скорость
- скорость
Знаки
![]() соответствуют
повороту решения на угол
соответствуют
повороту решения на угол
![]() .
.

Такой солитон называется КИНК.
«-» - носит название антикинк и движется налево.
Кинки движутся на
встречу друг другу, т.е. это уединенные
волны, сдвинутые на
![]() при
при
![]()
При столкновении они не аннигилируют и не осцилируют
Процесс столкновения
пререводит систему из состояния
![]() в состояние
в состояние
![]() .
При этом энергия конечна
.
При этом энергия конечна
-
Нелинейное уравнение Шредингера с кубической нелинейностью
![]()
Это уравнение тоже имеет солитонное решение
Применение: распространение сигналов по оптоволоконным каналам.
Решение имеет вид:
![]()

Уравнение Шредингера имеет множество интегралов (законов сохранения) и поэтому при столкновении солитоны не меняют свои амплитуду и скорость
-
Нелинейные уравнения, не имеющие решений в виде солитонов.
Наиболее показательное
уравнение - уравнение
![]() ( фи –четыре )
( фи –четыре )
Это нелинейное уравнение применяется в физике элементарных частиц
![]() ,
где
,
где![]() - параметр.
- параметр.
Для стационарной волны это уравнение можно решить.
Решение для этого уравнения примет имеет вид:
![]() ,
где
,
где
![]() ,
,
![]() -
некоторая постоянная фаза.
-
некоторая постоянная фаза.
Данное решение имеет форму кинка и похоже на решение уравнения sin-Гордана, но в отличие от Кингов и sin-Гордана при столкновении кинка и антикинка эти решения также образуют Кинги, но их амплитуда модулирована. Следовательно, данное уравнение не имеет решения в виде солитонов.
![]() при
при
![]()
![]() при
при
![]()
