6. Спектр ударной волны.

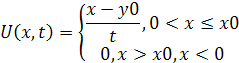
Будем считать .

Спектральная функция:

Отсюда следует, что спектральная функция убывает с ростом k (волновое число)

То ,что нельзя оборвать спектр при конечных k,это приведет к тому, что в спектре существуют сингулярные (бесконечные) разрывы.

Если перейти к сглаженному профилю, т.е. при конечной вязкости и числах Рейнольдса R>>1, в этом случае спектр гармоник можно эффективно обрезать при .

При этом эффективная ширинаспектральной функции будет оцениваться

Т.к. =>

2. Солитоны

1. Стационарные волны

Если задано некоторое волновое уравнение, причем неважно является ли оно линейным или нелинейным, оно может иметь решение в виде стационарной волны

Причем для линейного уравнения , а для нелинейного – зависит от амплитуды сигнала

Из класса нелинейных стационарных волн выделим уединенные волны. Уединенная волна характеризуется тем, что ее переход из одного предельного состояния в другое локализовано по .

РИСУНКИ Я не знаю надо или нет????????

2. Солитонные решения волнового уравнения (общие свойства)

Из всего многообразия уединенных волн выделяют солитонные решения.

Солито́н — структурно устойчивая, уединённая волна, распространяющаяся в нелинейной среде.

Опр.

Солитоном называется решение волнового уравнения в виде уединённой стационарной волны, которая при столкновении (взаимодействии) с другими такими же волнами асимптотически сохраняет свою форму и скорость.

Т.е солитоны ведут себя подобно частицам (частице подобная волна): при взаимодействии друг с другом или с некоторыми другими возмущениями они не разрушаются, а двигаются, сохраняя свою структуру неизменной. Это свойство может использоваться для передачи данных на большие расстояния без помех.

Интерпретация определения: пусть дано решение .

Допустим в начальный момент времени решение состоит из набора солитонных решений: , причем - соответствующая фаза данного солитона.

Допустим этот солитон через некоторое время взаимодействует с другими солитонами. Произойдет следующее: , , где

Линейное волновое уравнение 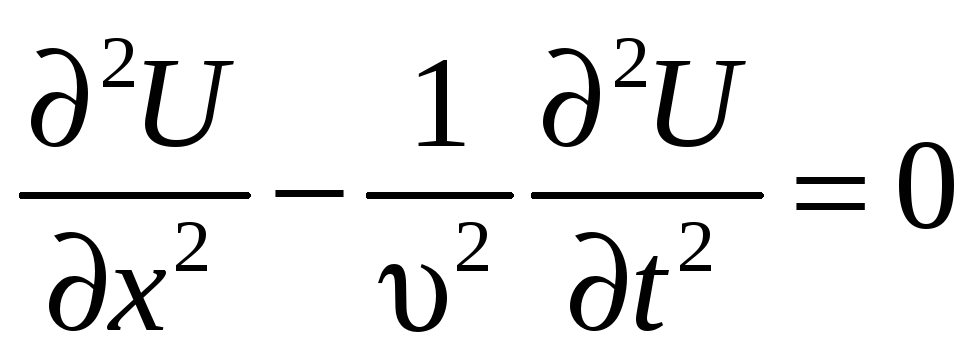может иметь солитонное решение, но не во всяком случае. В частности в среде без дисперсии (если среда с дисперсией – оно отсутствует).

В нелинейном уравнении существует солитонное решение только в среде с дисперсией. Т.е. солитонное решение является результатом конкуренции явлений укручения волны и дисперсии среды.

3. Солитонное решение уравнения Кортевега - де -Вриза

Уравнение Кортевега-де-Вриза (КДВ) впервые появилось, когда изучались длинные волны на мелкой воде (каналы).

. (а) – классический вид

. (б) - модифицированный

Слагаемые отражают нелинейность. А слагаемые связаны с дисперсией среды.

(Уравнение КДВ описывает нелинейные волны в жидкостях (движение по трубам), распределение электромагнитных импульсов по нервным волокнам человека, гидродинамические волны в плазме, включая космическую плазму, и т.д. )

Солитоном называют решение волнового уравнения в виде уединенной стационарной волны , которая при столкновении с другими такими же волнами асимптотически сохраняет свою форму и скорость.

Солитонные решения КДВ получили свое уравнение, исследуя распространение волн в одном направлении по поверхности мелкого канала.

- глубина канала (средняя величина);

При распространении глубина меняется , где мало и определяет положение поверхности канала на дно (отклонение).

Дифференциальное уравнение, описывающее движение волны имеет вид:

. (1)

Х – направление распространения

- гравитационная постоянная.

- произвольная постоянная;

, где- плотность жидкости;- поверхностное натяжение жидкости.

Сделаем замену переменных:

,

, (2)

придем к модифицированному виду уравнения КдВ:

. (3)

Причем для этого случая .Заменой можно перейти к любому .

Если в (3) сделать замену , то перейдем к классическому виду уравнения КдВ . (4)

Будем искать решение в виде стационарной волны , . (5)

- скорость бегущей волны.

Вычислим: , , . (6)

Подставим (6) в (4):

.

Проинтегрируем:

.

Т.к., получим , .

=>. (7)

Умножим на и проинтегрируем

. (8)

Получим

. (9)

Тогда решение: 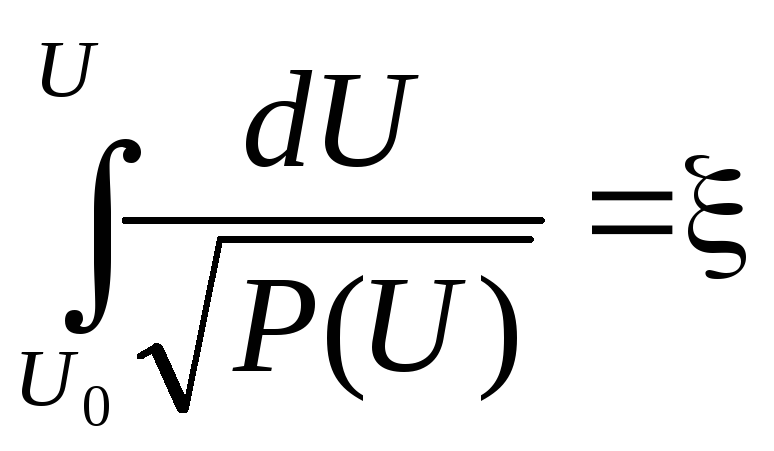(11) - эллиптический интеграл.

Способы решения:

1. (9)сводят преобразованиями к известным решениям среди трансцендентных функций

2. сводят к (11) и записывают его в виде некоторой трансцендентной функций

Решение зависит от корней полинома P(U). А корни кубического полинома зависят от граничных условий, т.е. от значений

Возьмем => (12)

Чтобы существовало действительное физическое решение было, должно быть .

В (12) единственный отрицательный сомножитель , при

То можно сделать преобразование и свести (9) к уравнениям, решением которых является эллиптические функции Якоби sn(z,k)

Введем параметр

Эта интегрируемая функция Якоби имеет асимптотические значения:

В зависимости от параметров получим в 1м случае – слабую колебательную волну, во 2м – солитон.

Т.к. уединенная волна локализована в некоторой области, то ее первая и вторая производные при будут равны нулю. Это будет означать, что для солитонного решения.

Полином (10) сильно упрощается

и интеграл можно взять.

Тогда решение будет:

(12) – решение в виде солитона.(это частное решение, удовлетворяющее краевым условиям )

Основные свойства солитонов уравнения КДВ

1. Амплитуда солитонов КДВ растет с ростом скорости (линейно). А его длительность обратно пропорциональна квадратному корню из скорости.

2. Знак решения в виде уединенной волны зависит от знака .

3. Уединенные волны уравнения КДВ однонаправлены, т.к. скорость не может быть отрицательной, т.к. 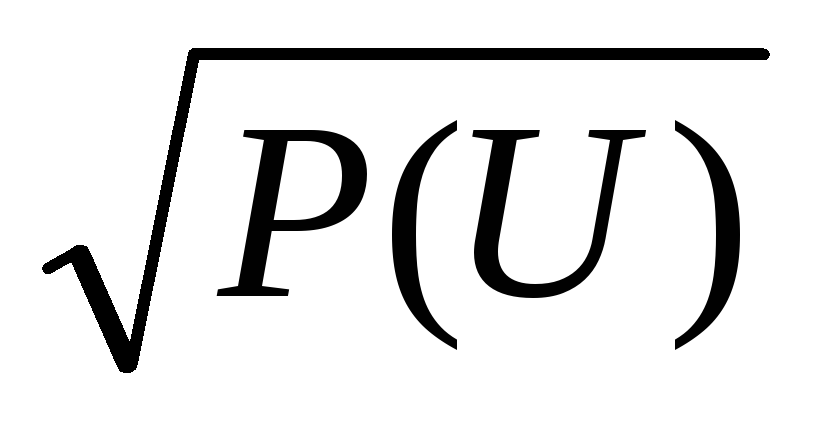должно быть действительным, а при .

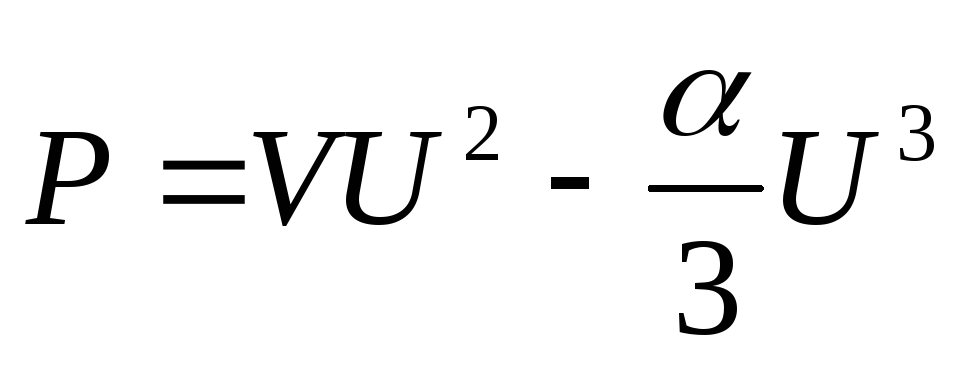Более общее решение уравнения (11) содержит и периодическую стационарную волну. Для получения этого решения следует взять ненулевые значения постоянных и определенным образом подобрать положение нулей .