
- •§ 16. Елементи теорії функцій комплексної змінної
- •16.1 Функції комплексної змінної.
- •16.1.1. Основні поняття
- •16.1.2 Границя і неперервність функції комплексної змінної
- •16.1.3. Основні елементарні функції комплексної змінної
- •16.1.3.1. Показникова функція
- •16.1.3.2. Логарифмічна функція
- •16.1.3.5. Тригонометричні функції
- •16.1.3.6. Гіперболічні функції
- •16.1.3.7. Обернені тригонометричні і гіперболічні функції
- •16.1.4. Диференціювання функції комплекснї змінної. Умови Ейлера-Даламбера.
- •16.1.5. Аналітична функція. Диференціал
- •16.1.6. Геометричний зміст модуля і аргумента похідної. Поняття про конформне відображення
- •Приклади конформних відображень, що здійснюються деякими елементарними функціями див. Додаток 1.
- •16.2. Інтегрування функції комплексної змінної
- •16.2.1 Означення, властивості і правила обчислення інтеграла
- •16.2.2. Теорема Коші. Первісна , невизначений інтеграл. Формула Ньютона-Лейбніца.
- •16.2.3. Інтеграл Коші. Інтегральна формула Коші
- •16.3. Ряди в комплексній площині
- •16.3.1. Числові ряди
- •16.3.2. Степеневі ряди
- •Ряд Тейлора
- •Нулі аналітичної функції
- •Ряд Лорана
- •Ряд Лорана для функції
- •○ Скористаємося відомим розкладом
- •16.3.6. Класифікація особливих точок. Зв'язок між нулем і полюсом функції
- •Усувні особливі точки
- •Істотно особлива точка
- •16.4. Лишок функції
- •16.4.1. Поняття лишка і основна теорема про лишки
- •16.4.2. Обчислення лишків. Застосування лишків в обчисленні інтегралів
16.4.2. Обчислення лишків. Застосування лишків в обчисленні інтегралів
Правильні або
усувні особливі точки. Очевидно, якщо
 є правильна або усувною особливою точкою
функції
є правильна або усувною особливою точкою
функції
 ,
то
,
то
 (в розкладі Лорана (3.11) у цих випадках
відсутня головна частина, тому
(в розкладі Лорана (3.11) у цих випадках
відсутня головна частина, тому
 ).
).
Полюс. Нехай
точка є простим полюсом функції
є простим полюсом функції
 .
Тоді ряд Лорана для функції
.
Тоді ряд Лорана для функції
 в околі точки
в околі точки
 має вигляд
має вигляд
 .
Звідси
.
Звідси
 .
.
Тому,
переходячи в цій рівності до границі
при
 ,
отримуємо
,
отримуємо
Res (4.3)
(4.3)
Зауваження.
Формулу (4.3) для обчислення лишка функції
 в простому полюсі можна подати в іншому
вигляді, якщо функція
в простому полюсі можна подати в іншому
вигляді, якщо функція
 є часткою двох функцій, аналітичних в
околі точки
є часткою двох функцій, аналітичних в
околі точки .
.
Нехай
 ,
де
,
де
 ,
а
,
а
 має простий нуль в
має простий нуль в
 (тобто
(тобто
 ,
,
 ).
Тоді, застосовуючи формулу (4.3), маємо:
).
Тоді, застосовуючи формулу (4.3), маємо:
 ,
тобто
,
тобто
Res (4.4)
(4.4)
Нехай точка є полюсом m-го порядку функції
є полюсом m-го порядку функції
 .
Тоді лоранівський розклад функції
.
Тоді лоранівський розклад функції
 в околі точки
в околі точки має вигляд
має вигляд
 .
Звідси
.
Звідси
 .
.
Диференціюючи
останню рівність
 раз, отримаємо:
раз, отримаємо:

 .
.
Переходячи тут до
границі при
 ,
отримуємо:
,
отримуємо:
Res (4.5)
(4.5)
Істотно особлива
точка. Якщо точка
 —
істотно особлива точка функції
—
істотно особлива точка функції
 ,
то для обчислення лишка функції в цій
точці зазвичай безпосередньо визначають
коефіцієнт
,
то для обчислення лишка функції в цій
точці зазвичай безпосередньо визначають
коефіцієнт
 в розкладі функції в ряд Лорана.
в розкладі функції в ряд Лорана.
Приклад 20.
Знайти лишки функції
 в її особливих точках.
в її особливих точках.
○ особливими
точками функції
 є:
є:
 —
простой полюс,
—
простой полюс,
 —
полюс третього порядку (
—
полюс третього порядку ( ). Отже, по формулі (4.4) маємо
). Отже, по формулі (4.4) маємо
 .
.
Використовуючи формулу (3.5) знаходимо:
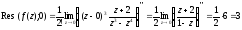 . ●
. ●
Приклад 21.
Знайти лишки функції
 в особливій точці
в особливій точці
 .
.
○ Лоранівський
розклад даної функції в околі точки
 було знайдено в прикладі 3.4. З нього
знаходимо
було знайдено в прикладі 3.4. З нього
знаходимо
 тобто
тобто
 .
.
Теорема про лишки часто використовується для обчислення інтеграла від функції комплексної змінної по замкненому контуру. ●
Приклад 22.
Обчислити
 ,
де L – коло
,
де L – коло


○
Функція
 має в крузі
має в крузі

(див.
рис. 20) простий полюс
 і полюс другого порядку
і полюс другого порядку
 .
Застосовуючи формули (4.2), (4.3) і (4.5)
отримуємо:
.
Застосовуючи формули (4.2), (4.3) і (4.5)
отримуємо:
Рис. 20



Визначений
інтеграл вигляду
 за допомогою заміни
за допомогою заміни
 в деяких випадках вдається перетворити
в інтеграл по замкнутому контурі
в деяких випадках вдається перетворити
в інтеграл по замкнутому контурі
 від функції комплексної змінної, до
якого уже застосовна основна теорема
про лишки. ●
від функції комплексної змінної, до
якого уже застосовна основна теорема
про лишки. ●
Приклад 23.
Обчислити за допомогою лишків інтеграл
 .
.
○ Зробимо заміну
змінних, поклавши
 .
Тоді
.
Тоді
 ,
,
 .
При зміні x від 0 до 2
точка z опише в додатньому напрямку
коло
.
При зміні x від 0 до 2
точка z опише в додатньому напрямку
коло
 .
Отже,
.
Отже,
 .
.
У
крузі
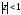 функція
функція
 має полюс другого порядку
має полюс другого порядку
 .
За формулою (4.5) знаходимо
.
За формулою (4.5) знаходимо


 .
.
Отже,
 .
●
.
●
